Handbook/B Language
Current Limitations
ProB in general requires all deferred sets to be given a finite cardinality. If no cardinality is specified, a default size will be used. Also, unless finite bounds can be inferred by the ProB constraint solver, mathematical integers will only be enumerated within MININT to MAXINT (and ProB will generate enumeration warnings in case no solution is found).
Other general limitations are:
- Trees and binary trees. These constructs are specific to the AtelierB tool and are only partially supported;
- Definitions. Definitions (from the DEFINITIONS clause) with arguments are supported, but in contrast to AtelierB they are parsed independently and have to be either an expression, a predicate, or a substitution; definitions which are predicates or substitutions must be declared before first use. Also: the arguments of DEFINITIONS have to be expressions. Finally, when replacing DEFINITIONS the associativity is not changed. E.g., with PLUS(x,y) == x+y, the expression PLUS(2,3)*10 will evaluate to 50 (and not to 32 as with Atelier-B).
Also, ProB will generate a warning when variable capture may occur.
- There are also limitations with refinements. See below;
- VALUES This clause of IMPLEMENTATION machines is not yet fully supported;
- Parsing: ProB will require parentheses around the comma, the relational composition, and parallel product operators. For example, you cannot write r2=rel;rel. You need to write r2=(rel;rel). This allows ProB to distinguish the relational composition from the sequential composition (or other uses of the semicolon). You also generally need to put BEGIN and END around the sequential composition operator, e.g., Op = BEGIN x:=1;y:=2 END.
See the page Using ProB with Atelier B for more details.
Multiple Machines and Refinements
It is possible to use multiple classical B machines with ProB. However, ProB may not enforce all of the classical B visibility rules (although we try to). As far as the visibility rules are concerned, it is thus a good idea to check the machines in another B tool, such as Atelier B or the B-Toolkit.
While refinements are supported, the preconditions of operations are not propagated down to refinement machines. This means that you should rewrite the preconditions of operations (and, if necessary, reformulate them in terms of the variables of the refinement machine). Also, the refinement checker does not yet check the gluing invariant.
Note however, that for Rodin Event-B models we now support multi-level animation and validation.
Summary of B Syntax
Summary of B Syntax
Below we describe the "classical" B syntax as supported by ProB. You may also wish to consult
- The B summary by Ken Robinson (File:B-summary.pdf)
- The Atelier-B reference manual (b-language-reference-manual.pdf)
Logical predicates
P & Q conjunction P or Q disjunction P => Q implication P <=> Q equivalence not(P) negation !(x).(P=>Q) universal quantification #(x).(P&Q) existential quantification btrue truth (this is a predicate) bfalse falsity (this is a predicate)
Above, P and Q stand for predicates. Inside the universal quantification, P must give a value type to the quantified variable. Note: you can also introduce multiple variables inside a universal or existential quantification, e.g., !(x,y).(P => Q).
Equality
E = F equality E /= F disequality
Booleans
TRUE truth value (this is an expression)
FALSE falsity value (this is an expression)
BOOL set of boolean values ({TRUE,FALSE})
bool(P) convert predicate into BOOL value
Warning: TRUE and FALSE are expression values and not predicates in B and cannot be combined using logical connectives. To combine two boolean values x and y using conjunction you have to write x=TRUE & y=TRUE. To convert a predicate such as z>0 into a boolean value you have to use bool(z>0).
Sets
{} empty set
{E} singleton set
{E,F} set enumeration
{x|P} comprehension set
{(x).P|E} Event-B style comprehension set (brackets needed)
POW(S) power set
POW1(S) set of non-empty subsets
FIN(S) set of all finite subsets
FIN1(S) set of all non-empty finite subsets
card(S) cardinality
S*T cartesian product
S\/T set union
S/\T set intersection
S-T or S \ T set difference
E:S element of
E/:S not element of
S<:T subset of
S/<:T not subset of
S<<:T strict subset of
S/<<:T not strict subset of
union(S) generalised union over sets of sets
inter(S) generalised intersection over sets of sets
UNION(z).(P|E) generalised union with predicate
INTER(z).(P|E) generalised intersection with predicate
Integers
INTEGER set of integers NATURAL set of natural numbers NATURAL1 set of non-zero natural numbers INT set of implementable integers (MININT..MAXINT) NAT set of implementable natural numbers NAT1 set of non-zero implementable natural numbers n..m set of numbers from n to m MININT the minimum implementable integer MAXINT the maximum implementable integer m>n greater than m<n less than m>=n greater than or equal m<=n less than or equal max(S) maximum of a set of numbers min(S) minimum of a set of numbers m+n addition m-n difference m*n multiplication m/n division m**n power m mod n remainder of division PI(z).(P|E) set product SIGMA(z).(P|E) set summation succ(n) successor (n+1) pred(n) predecessor (n-1) 0xH hexadecimal literal, where H is a sequence of letters in [0-9A-Fa-f]
Relations
S<->T relation
S<<->T total relation
S<->>T surjective relation
S<<->>T total surjective relation
E|->F maplet
dom(r) domain of relation
ran(r) range of relation
id(S) identity relation
S<|r domain restriction
S<<|r domain subtraction
r|>S range restriction
r|>>S range subtraction
r~ inverse of relation
r[S] relational image
r1<+r2 relational overriding (r2 overrides r1)
r1><r2 direct product (all pairs (x,(y,z)) with x,y:r1 and x,z:r2)
(r1;r2) relational composition {x,y| x|->z:r1 & z|->y:r2}
(r1||r2) parallel product (all pairs ((x,v),(y,w)) with x,y:r1 and v,w:r2)
prj1(S,T) projection function (usage prj1(Dom,Ran)(Pair))
prj2(S,T) projection function (usage prj2(Dom,Ran)(Pair))
prj1(Pair) and prj2(Pair) are also allowed
fnc(r) translate relation A<->B into function A+->POW(B)
rel(r) translate relation A<->POW(B) into relation A<->B
closure1(r) transitive closure
closure(r) reflexive & transitive closure
(equal to id(TYPEOF_r) \/ closure1(r))
iterate(r,n) iteration of r with n>=0
(Note: iterate(r,0)=id(s) where s=TYPEOF_r)
Functions
S+->T partial function S-->T total function S+->>T partial surjection S-->>T total surjection S>+>T partial injection S>->T total injection S>+>>T partial bijection S>->>T total bijection %x.(P|E) lambda abstraction f(E) function application f(E1,...,En) is also supported (as well as f(E1|->E2...|->En))
Sequences
[] or <> empty sequence [E] singleton sequence [E,F] constructed sequence seq(S) set of sequences over S seq1(S) set of non-empty sequences over S iseq(S) set of injective sequences over S iseq1(S) set of non-empty injective sequences over S perm(S) set of bijective sequences (permutations) over S size(s) size of sequence s^t concatenation E->s prepend element s<-E append element rev(s) reverse of sequence first(s) first element last(s) last element front(s) front of sequence (all but last element) tail(s) tail of sequence (all but first element) conc(S) concatenation of sequence of sequences s/|\n take first n elements of sequence s\|/n drop first n elements from sequence
Records
struct(ID:S,...,ID:S) set of records with given fields and field types rec(ID:E,...,ID:E) construct a record with given field names and values E'ID get value of field with name ID
Identifiers
ID must start with letter (ASCII or Unicode), can then contain
letters (ASCII or Unicode), digits and underscore (_) and
can end with Unicode subscripts followed by Unicode primes
M.ID composed identifier for identifier coming from included machine M
`ID` an identifier in backquotes can contain almost any character (except newline)
Strings
"astring" a specific (single-line) string value
'''astring''' an alternate way of writing (multi-line) strings, no need to escape "
```tstring``` template strings, where ${Expr} parts are evaluated and converted to string,
you can provide options separated by commas in square brackets like $[2f]{Expr}.
Valid options are: Nf (for floats/reals), Nd (for integer), Np (padding),
ascii (can be abbreviated to a), unicode (can be abbreviated to u).
STRING the set of all strings
Atelier-B does not support any operations on strings, apart from equality and disequality. In ProB, however, some of the sequence operators work also on strings:
size(s) the length of a string s rev(s) the reverse of a string s s ^ t the concatenation of two strings conc(ss) the concatenation of a sequence of strings
You can turn this support off using the STRING_AS_SEQUENCE preference. The library LibraryStrings.def in stdlib contains additional useful external functions (like TO_STRING, STRING_SPLIT, FORMAT_TO_STRING, INT_TO_HEX_STRING, ...).
ProB also allows multi-line strings.
As of version 1.7.0, ProB will support the following escape sequences within strings:
\n newline (ASCII character 13) \r carriage return (ASCII 10) \t tab (ASCII 9) \" the double quote symbol " \' the single quote symbol ' \\ the backslash symbol
Within single-line string literals, you do not need to escape '. Within multi-line string literals, you do not need to escape " and you can use tabs and newlines.
ProB assumes that all B machines and strings use the UTF-8 encoding.
Reals
REAL set of reals FLOAT set of floating point numbers i.f real literal in decimal notation, where i and f are natural numbers i.fEg real literal in scientific notation, where i,f are natural numbers and g is an integer real(n) convert an integer n into a real number floor(r) convert a real r into an integer ceiling(r) convert a real r into an integer
One can also use a lowercase e for literals in scientific notation (e.g. 1.0e-10). Standard arithmetic operators can be applied to reals: +, - , *, /, SIGMA, PI. Exponentiation of a real with an integer is also allowed. The comparison predicates =, /=, <, >, <=, >= also all work. Support for reals and floats is experimental. The definition in Atelier-B is also not stable yet. Currently ProB supports floating point numbers only. Warning: properties such as associativity and commutativity of arithmetic operators thus do not hold. The library LibraryReals.def in stdlib contains additional useful external functions (like RSIN, RCOS, RLOG, RSQRT, RPOW, ...). You can turn off support for REALS using the preference ALLOW_REALS. The REAL_SOLVER preference how constraints are solved.
Trees
Nodes in the tree are denoted by index sequences (branches), e.g, n=[1,2,1] Each node in the tree is labelled with an element from a domain S. A tree is a function mapping of branches to elements of the domain S.
tree(S) set of trees over domain S btree(S) set of binary trees over domain S top(t) top of a tree const(E,s) construct a tree from info E and sequence of subtrees s rank(t,n) rank of the node at end of branch n in the tree t father(t,n) father of the node denoted by branch n in the tree t son(t,n,i) the ith son of the node denoted by branch n in tree t sons(t) the sequence of sons of the root of the tree t subtree(t,n) arity(t,n) bin(E) construct a binary tree with a single node E bin(tl,E,tr) construct a binary tree with root info E and subtrees tl,tr left(t) the left (first) son of the root of the binary tree t right(t) the right (last) son of the root of the binary tree t sizet(t) the size of the tree (number of nodes) prefix(t) the nodes of the tree t in prefix order postfix(t) the nodes of the tree t in prefix order mirror, infix are recognised by the parser but not yet supported by ProB itself
LET and IF-THEN-ELSE
ProB allows the following for predicates, expressions and substitutions:
IF P THEN E1 END conditional branching IF P THEN E1 ELSIF E2 END we also allow multiple ELSIF branches IF P THEN E1 ELSE E2 END but you always need an ELSE branch for expressions and predicates IF P THEN E1 ELSIF E2 ELSE E3 END LET x1,... BE x1=E1 & ... IN E END introduce local variables
Note: the expression Ei defining xi is allowed to use x1,...,x(i-1) for predicates/expressions. By setting the preference ALLOW_COMPLEX_LETS to TRUE, this is also allowed for substitutions.
Statements (aka Substitutions)
skip no operation x := E assignment f(x) := E functional override x :: S choice from set x : (P) choice by predicate P (constraining x; previous value of x is x$0) x <-- OP(x) call operation and assign return value G||H parallel substitution** G;H sequential composition** ANY x,... WHERE P THEN G END non deterministic choice LET x,... BE x=E & ... IN G END VAR x,... IN G END generate local variables PRE P THEN G END ASSERT P THEN G END CHOICE G OR H END IF P THEN G END IF P THEN G ELSE H END IF P1 THEN G1 ELSIF P2 THEN G2 ... END IF P1 THEN G1 ELSIF P2 THEN G2 ... ELSE Gn END SELECT P THEN G WHEN ... WHEN Q THEN H END SELECT P THEN G WHEN ... WHEN Q THEN H ELSE I END CASE E OF EITHER m THEN G OR n THEN H ... END END CASE E OF EITHER m THEN G OR n THEN H ... ELSE I END END WHILE P1 DO G INVARIANT P2 VARIANT E END WHEN P THEN G END is a synonym for SELECT P THEN G END
**: cannot be used at the top-level of an operation, but needs to be wrapped inside a BEGIN END or another statement (to avoid confusion with the operators ; and || on relations).
Machine header
MACHINE or REFINEMENT or IMPLEMENTATION
Note: machine parameters can either be SETS (if identifier is all upper-case) or scalars (i.e., integer, boolean or SET element; if identifier is not all upper-case; typing must be provided be CONSTRAINTS)
You can also use MODEL or SYSTEM as a synonym for MACHINE, as well as EVENTS as a synonym for OPERATIONS. ProB also supports the ref keyword of Atelier-B for event refinement.
Machine sections
CONSTRAINTS P (logical predicate)
SETS S;T={e1,e2,...};...
FREETYPES x=x1,x2(arg2),...;...
CONSTANTS x,y,...
CONCRETE_CONSTANTS cx,cy,...
PROPERTIES P (logical predicate)
DEFINITIONS m(x,...) == BODY;...
VARIABLES x,y,...
CONCRETE_VARIABLES cv,cw,...
INVARIANT P (logical predicate)
ASSERTIONS P;...;P (list of logical predicates separated by ;)
INITIALISATION S (substitution)
OPERATIONS O;... (operations)
Machine inclusion
USES list of machines INCLUDES list of machines SEES list of machines EXTENDS list of machines PROMOTES list of operations REFINES machine
Note: Refinement machines should express the operation preconditions in terms of their own variables.
Definitions
NAME1 == Expression; Definition without arguments NAME2(ID,...,ID) == E2; Definition with arguments "FILE.def"; Include definitions from file
There are a few specific definitions which can be used to influence ProB:
GOAL == P to define a custom Goal predicate for Model Checking
(the Goal is also set by using "Advanced Find...")
SCOPE == P to limit the search space to "interesting" nodes
scope_SETNAME == n..n to define custom cardinality for set SETNAME
scope_SETNAME == n equivalent to 1..n
SET_PREF_MININT == n
SET_PREF_MAXINT == n
SET_PREF_MAX_INITIALISATIONS == n max. number of intialisations computed
SET_PREF_MAX_OPERATIONS == n max. number of enablings per operation computed
MAX_OPERATIONS_OPNAME == n max. number of enablings for the operation OPNAME
SET_PREF_SYMBOLIC == TRUE/FALSE
SET_PREF_TIME_OUT == n time out for operation computation in ms
ASSERT_LTL... == "LTL Formula" using X,F,G,U,R LTL operators +
Y,O,H,S Past-LTL operators +
atomic propositions: e(OpName), [OpName], {BPredicate}
HEURISTIC_FUNCTION == n in directed model-checking mode nodes with smalles value will be processed first
The following definitions allow providing a custom state visualization (n can be empty or a number):
ANIMATION_FUNCTIONn == e a function (INT*INT) +-> INT or an INT
ANIMATION_FUNCTION_DEFAULT == e a function (INT*INT) +-> INT or an INT
instead of any INT above you can also use BOOL or any SET
as a result you can also use STRING values,
or even other values which are pretty printed
ANIMATION_IMGn == "PATH to .gif" a path to a gif file
ANIMATION_STRn == "sometext" a string without spaces;
the result integer n will be rendered as a string
ANIMATION_STR_JUSTIFY_LEFT == TRUE computes the longest string in the outputs and pads
the other strings accordingly
SET_PREF_TK_CUSTOM_STATE_VIEW_PADDING == n additional padding between images in pixels
SET_PREF_TK_CUSTOM_STATE_VIEW_STRING_PADDING == n additional padding between text in pixels
The following definitions allow providing a custom state graph (n can be empty or a number):
CUSTOM_GRAPH_NODESn == e define a set of nodes to be shown,
nodes can also be pairs (Node,Colour), triples (Node,Shape,Colour) or
records or sets of records like
rec(color:Colour, shape:Shape, style:Style, label:Label, value:Node, ...)
Colours are strings of valid Dot/Tk colors (e.g., "maroon" or "red")
Shapes are strings of valid Dot shapes (e.g., "rect" or "hexagon"), and
Styles are valid Dot shape styles (e.g., "rounded" or "solid" or "dashed")
CUSTOM_GRAPH_EDGESn == e define a relation to be shown as a graph
edges can either be pairs (node1,node2) or triples (node1,Label,node2)
where Label is either a Dot/Tk color or a string or value representing
the label to be used for the edges
In both cases e can also be a record which defines default dot attributes like color, shape, style and description, e.g.:
CUSTOM_GRAPH_NODES == rec(color:"blue", shape:"rect", style:"filled", nodes:e); CUSTOM_GRAPH_EDGES == rec(color:"red", style:"dotted", dir:"none", penwidth:2, edges:e)
Alternatively, the complete graph can be put into one definition using CUSTOM_GRAPH.
You have to define a single CUSTOM_GRAPH definition of a record with global graph attributes
(like rankdir or layout) and optionally with edges and nodes attributes (replacing CUSTOM_GRAPH_EDGES and CUSTOM_GRAPH_NODES respectively), e.g.:
CUSTOM_GRAPH == rec(layout:"circo", nodes:mynodes, edges:myedges)
You can now also use a single CUSTOM_GRAPH definition of a record with global graph attributes (like rankdir or layout) and optionally with edges and nodes attributes (replacing CUSTOM_GRAPH_EDGES and CUSTOM_GRAPH_NODES respectively), e.g.:
CUSTOM_GRAPH == rec(layout:"circo", nodes:mynodes, edges:myedges)
You can also provide SEQUENCE_CHART_opname definitions for generating UML sequence charts.
These DEFINITIONS affect VisB:
VISB_JSON_FILE == "PATH to .json" a path to a default VisB JSON file for visualisation;
if it is "" an empty SVG will be created
VISB_SVG_OBJECTSn == ... define a record or set of records for creating new SVG objects
VISB_SVG_UPDATESn == ... define a record or set of records containing updates of SVG objects
VISB_SVG_HOVERSn == ... define a record or set of records for VisB hover functions
VISB_SVG_BOX == ... record with dimensions (height, width) of a default empty SVG
VISB_SVG_CONTENTS == ... defines a string to be included into a created empty SVG file
Comments and Pragmas
B supports two styles of comments: /* ... */ block comments // ... line comments
ProB recognises several pragma comments of the form /*@ PRAGMA VALUE */ The whitespace between @ and PRAGMA is optional.
/*@symbolic */ put before comprehension set, lambda, union or composition to instruct ProB
to keep it symbolic and not try to compute it explicitly
/*@label LBL */ associates a label LBL with the following predicate
(LBL must be identifier or a string "....")
/*@desc DESC */ associates a description DESC with the preceding predicate or
introduced identifier (in VARIABLES, CONSTANTS,... section)
There are three special descriptions:
/*@desc memo*/ to be put after identifiers in the ABSTRACT_CONSTANTS section
indicating that these functions should be memoized
/*@desc expand*/ to be put after identifiers (in VARIABLES, CONSTANTS,... section)
indicating that they should be expanded and not kept symbolically
/*@desc prob-ignore */ to be put after predicates (e.g., in PROPERTIES) which
should be ignored by ProB
when the preference USE_IGNORE_PRAGMAS is TRUE
You can also add description to an operation at the end of the operation body.
This description can be viewed in ProB Tcl/Tk, ProB2-UI and in the HTML trace exports.
Note: this description can contain ${Expr} template string expressions which reference parameter
and variable values to provide a specific description for each operation execution.
/*@file PATH */ associates a file for machines in SEES, INCLUDES, ...
put pragma after a seen or included machine
/*@package NAME */ at start of machine, machine file should be in folder NAME/...
NAME can be qualified N1.N2...Nk, in which case the machine
file should be in N1/N2/.../Nk
/*@import-package NAME */ adds ../NAME to search paths for SEES,...
NAME can also be qualified N1.N2...Nk, use after package pragma
/*@generated */ can be put at the top of a machine file; indicates the machine
is generated from some other source
File Extensions
.mch for abstract machine files .ref for refinement machines .imp for implementation machines .def for DEFINITIONS files .rmch for Rules machines for data validation
Free Types
More information can be found here.
Free types exist in Z and in the Rodin theory plugin and are supported by ProB. You can also define new free types in classical B by adding a FREETYPES clause with free type definitions separated by semicolon.
Here is a definition of an inductive type IntList for lists of integers constructed using inil and icons:
FREETYPES IntList = inil, icons(INTEGER*IntList)
Differences with AtelierB/B4Free
Basically, ProB tries to be compatible with Atelier B and conforms to the semantics of Abrial's B-Book and of Atelier B's reference manual. Here are the main differences with Atelier B:
- tuples without parentheses are not supported; write (a,b,c) instead of a,b,c
- relational composition has to be wrapped into parentheses; write (f;g)
- parallel product also has to be wrapped into parentheses; write (f||g)
- not all tree operators are supported
- the VALUES clause is only partially supported
- definitions have to be syntactically correct and be either an expression,
predicate or substitution;
the arguments to definitions have to be expressions;
definitions which are predicates or substitutions must be declared before first use
- definitions are local to a machine
- for ProB the order of fields in a record is not relevant (internally the fields are
sorted), Atelier-B reports a type error if the order of the name of the fields changes
- for ProB closure(X) = id(TypeOfX) \/ closure1(X), i.e., closure({1|->2}) contains
1|->1, 2|->2 but also 3|->3, 4|->4, ... This corresponds to the definition in
Abrial's B-Book, but Atelier-B's definition does not cotain 3|->3, 4|->4, ...
- well-definedness: for disjunctions and implications ProB uses the L-system
of well-definedness (i.e., for P => Q, P should be well-defined and
if P is true then Q should also be well-defined)
- ProB allows WHILE loops and sequential composition in abstract machines
- ProB now allows the IF-THEN-ELSE and LET for expressions and predicates
(e.g., IF x<0 THEN -x ELSE x END or LET x BE x=f(y) IN x+x END)
- ProB's type inference is stronger than Atelier-B's, much less typing predicates
are required
- You can apply prj1 and prj2 without providing the type arguments, e.g., prj2(prj1(1|->2|->3))
- ProB accepts operations with parameters but without pre-conditions
- ProB allows identifiers consisting of a single character and identifiers in single backquotes (`id`)
- ProB allows to use <> for the empty sequence (but this use is deprecated)
- ProB allows escape codes (\n, \', \", see above) and supports UTF-8 characters in strings,
and ProB allows multi-line string literals written using three apostrophes ('''string''')
as well as template strings using three backquotes (e.g., ```1+2=${1+2}```)
- ProB allows a she-bang line in machine files starting with #!
- ProB allows btrue and bfalse as predicates in B machines
- ProB allows to use the Event-B relation operators <<->, <->>, <<->>
- ProB allows set comprehensions with an extra expression like {x•x:1..10|x*x}.
- The FREETYPES section and the external libraries (LibraryStrings.def, ...) do not exist in Atelier-B
See also our Wiki for documentation:
Also note that there are various differences between BToolkit and AtelierB/ProB:
- AtelierB/ProB do not allow true as predicate; e.g., PRE true THEN ... END is not allowed (use BEGIN ... END instead) ProB now allows btrue and bfalse to be used as predicates. - AtelierB/ProB do not allow a machine parameter to be used in the PROPERTIES - AtelierB/ProB require a scalar machine parameter to be typed in the CONSTRAINTS clause - In AtelierB/ProB the BOOL type is pre-defined and cannot be redefined
If you discover more differences, please let us know!
Other notes
ProB now supports the Unicode mathematical symbols, exactly like Atelier-B ProB is best at treating universally quantified formulas of the form !x.(x:SET => RHS), or !(x,y).(x|->y:SET =>RHS), !(x,y,z).(x|->y|->z:SET =>RHS), ...; otherwise the treatment of !(x1,...,xn).(LHS => RHS) may delay until all values treated by LHS are known. Similarly, expressions of the form SIGMA(x).(x:SET|Expr) and PI(x).(x:SET|Expr) lead to better constraint propagation. The construction S:FIN(S) is recognised by ProB as equivalent to the Event-B finite(S) operator. ProB assumes that machines and STRING values are encoded using UTF-8.
Event-B Syntax
Note that the Event-B syntax in Rodin is slightly different (e.g, no sequences or strings built-in). There is also an Event-B summary by Ken Robinson (File:EventB-summary.pdf). The Event-B syntax is only available for Event-B models in Rodin, ProB2-UI and ProB Jupyter notebooks.
Feedback
Please help us to improve this documentation by providing feedback in our bug tracker, asking questions in our prob-users group or sending an email to Michael Leuschel.
Types
| Warning This page has not yet been reviewed. Parts of it may no longer be up to date |
ProB requires all constants and variables to be typed. As of version 1.3, ProB uses a new unification-based type inference and checking algorithm. As such, you should be able to use most Atelier B models without problem. On the other hand, certain models that ProB accepts will have to be rewritten to be type checked by Atelier B (e.g., by adding additional typing predicates). Also note that, in contrast to Atelier B, ProB will type check macro DEFINITIONS.
What is a basic type in B
- BOOL
- INTEGER
- Any name of a set introduced in a SETS clause or introduced as a parameter of the machine
- POW (τ) (power set) for τ being a type
- τ1 * τ2 (Cartesian product) for τ1 and τ2 being two types
What needs to be typed
Generally speaking, any constant or variable. More precisely:
- Constants declared in the CONSTANTS clause must be typed in the PROPERTIES clause;
- Variables declared in the VARIABLES clause must be typed in the INVARIANT;
- Arguments of an operation must be typed in the precondition PRE or a top-level SELECT statement of the operation;
- Variables in universal or existential quantifications;
- Variables of set comprehensions must be typed in a conjunct of the body of the set comprehension. For example, {xx | xx:NAT & xx>0 & xx<5} is fine, but {xx | xx>0 & xx<5} is not;
- Variables of lambda abstractions must be typed in the predicate part of the abstraction. For example, %yy.(yy:NAT|yy-1) properly types the variable yy;
- Variables introduced in ANY statements must be typed in the WHERE part of the statement.
ProB will warn you if a variable has not been given a type.
HINT: The Analyse|Show Typing command reveals the typing that ProB has inferred for your constants and global variables.
Restriction on the Domains of the Variables
Animating and verifying a B specification is in principle undecidable. ProB overcomes this by requiring that the domain of the variables is finite (i.e., with finitely many values) or integer. This ensures that the state space has finite size. Typing of the B specification ensures this restriction.
In the B specification, a set is either defined explicitely, thus being a finite domain, or its definition is deferred. In the later case, the user can indicate the size of the set mySET (without defining its elements) by creating a macro in the DEFINITIONS clause with the name scope_mySET and an integer value (e.g. scope_mySET==2) or a value specified as a range (e.g. scope_mySET == 1..12). The macros with the prefix "scope_" will be used by ProB and do not modify the B specification. If the size of the set is unspecified, ProB considers the set to have a default size. The value for the default size is defined in the Preferences|Animation Preferences... preference window by the preference Size of unspecified sets in SETS section.
The B method enables to specify the size of a set with the card operator in the PROPERTIES clause; this form of constraint is now supported by ProB, provided it is of a simple form card(S)=Nr, where S is a deferred set and Nr a natural number.
Enumeration in ProB
The typing information is used by ProB to enumerate the possible values of a constant or a variable whenever a specification does not narrow down that value to a single value.
For example, if you write xx:NAT & xx=1 ProB does not have to resort to enumeration as the xx=1 constraint imposes a single possible value for xx. However, if you write xx:NAT & xx<3 ProB will enumerate the possible values of xx in order to find those that satisfy the constraints imposed by the machine (here 0,1,2).
ProB will use the constraints to try to cut down the enumeration space, and will resort to enumeration usually only as a last resort. So something like xx:NAT & xx<10 & x>2 & x=5 will not result in enumeration.
The enumeration range for integers is controlled by two preferences in the Preferences|Animation Preferences... preference window: !MinInt, used for expressions such as xx::INT, and !MaxInt, used for expressions such as xx::NAT preferences. Nevertheless, writing xx: NAT & xx = 55 puts the value 55 in x no matter what !MaxInt is set to, as no enumeration is required.
Note that these preferences also apply to the mathematical integers (INTEGER) and natural numbers (NATURAL). In case a mathematical integer or natural number is enumerated (using !MinInt and !MaxInt) a warning is printed on the console.
Deferred Sets
A deferred set in B is declared in the SETS Section and is not explicitly enumerated. In the example below, AA is a deferred set and BB is an enumerated set.
MACHINE M0
SETS AA; BB={bb,cc,dd}
END
ProB in general requires all deferred sets to be given a finite cardinality before starting animation or model checking. If no cardinality is specified, a default size will be used (which is controlled by the DEFAULT_SETSIZE preference).
In general (for both probcli and ProB Tcl/Tk) you can set the cardinality of a set AA either by
- making it an enumerated set, i.e., adding AA = {v1,v2,…} to the SETS clause
- adding a predicate card(AA) = constant to the PROPERTIES clause
- Note: various other predicates in the PROPERTIES clause will also influence the size used for AA by ProB, for example:
- card(AA) > 1
- aa:AA & bb:AA & aa/=bb
- AA = {aa,bb} & aa/=bb
- …
- you can add a DEFINITION scope_AA == constant to instruct ProB to set the cardinality of AA to the constant.
Using Refinement for Animation Preferences
Note: instead of adding AA = {aa,bb} to the SETS clause you can also add AA = {aa,bb} & aa/=bb to the PROPERTIES clause. This can also be done in a refinement. A good idea is then to generate a refinement for animation with ProB (which may contain other important settings for animation):
REFINEMENT M0_ProB REFINES M0
CONSTANTS aa,bb
PROPERTIES
AA = {aa,bb} & aa/=bb
END
Setting Deferred Set Cardinalities within probcli
From the command-line, using probcli you can use the command-line switch:
-card <GS> <VAL>
Example:
probcli my.mch -card PID 5
Free Types
Summary
Free types exist in Z and in the Rodin theory plugin and are supported by ProB. You can also define new free types in classical B by adding a FREETYPES clause with free type definitions separated by semicolon.
Here is a definition of an inductive type IntList for lists of integers constructed using inil and icons:
FREETYPES IntList = inil, icons(INTEGER*IntList)
What is a Free Type
Free types are sum types [1]. They make it easier to define recursive structures. A free type value may take exactly one of the defined subtypes, with additional payload data, and later the exact subtype can be queried and the payload data retrieved.
Syntax
FREETYPES
The FREETYPES machine clause contains a semicolon separated list of Freetype Definitions:
FREETYPES <Freetype Definition 1>; ...; <Freetype Definition N>
Freetype Definition
Each Freetype Definition consists of an identifier (the name of the free type), followed by an equals symbol and one or more Freetype Constructors separated by commas:
<Identifier> = <Freetype Constructor 1>, ..., <Freetype Constructor N>
Freetype Constructor
A Freetype Constructor may be a single identifier (the name of the free type constructor) or an identifier with a single expression argument (the type of the payload data) in parentheses.
<Identifier> <Identifier>(<Expression>)
Semantics
The name of the free type can be used anywhere in the machine as a type identifier (like a set) to define the type of a value.
To actually create a value of the free type one needs to use one of the free type constructors. Free type constructors that do not take an argument can be used as the right side of an assignment as-is, while free type constructors that have an argument need a value parameter of that type - this works like a function call. Because those constructor calls work like function calls, we benefit from the tuple-function syntactic sugar and can use one tuple parameter as a way to represent multiple logical parameters and call the constructor with values separated by commas without having to create a tuple first.
Internally constructors without parameter are just values, while constructors with parameters are functions that take the payload data and return the free type value with the given payload. To check whether a free type value has a specific subtype one can use equality for parameter-less constructors and membership in the range for constructors with a parameter.
To get the contained value out of a free type value one can use the inverse constructor (also called deconstructor), simply created by applying the B operator ~.
Example
In our example from the introduction we have a free type with two constructors that represents a list. The constructor inil represents an empty list and takes no argument, while the icons constructor represents a list head with the first value and the rest of the list combined as a tuple.
To create a list with content we are using the simplified function call syntax, so we do not have to construct the tuple (head, tail) directly.
To get values out of the icons subtype we use the the deconstructor icons~. The resulting value is a tuple which we need to project to the first or second value respectively.
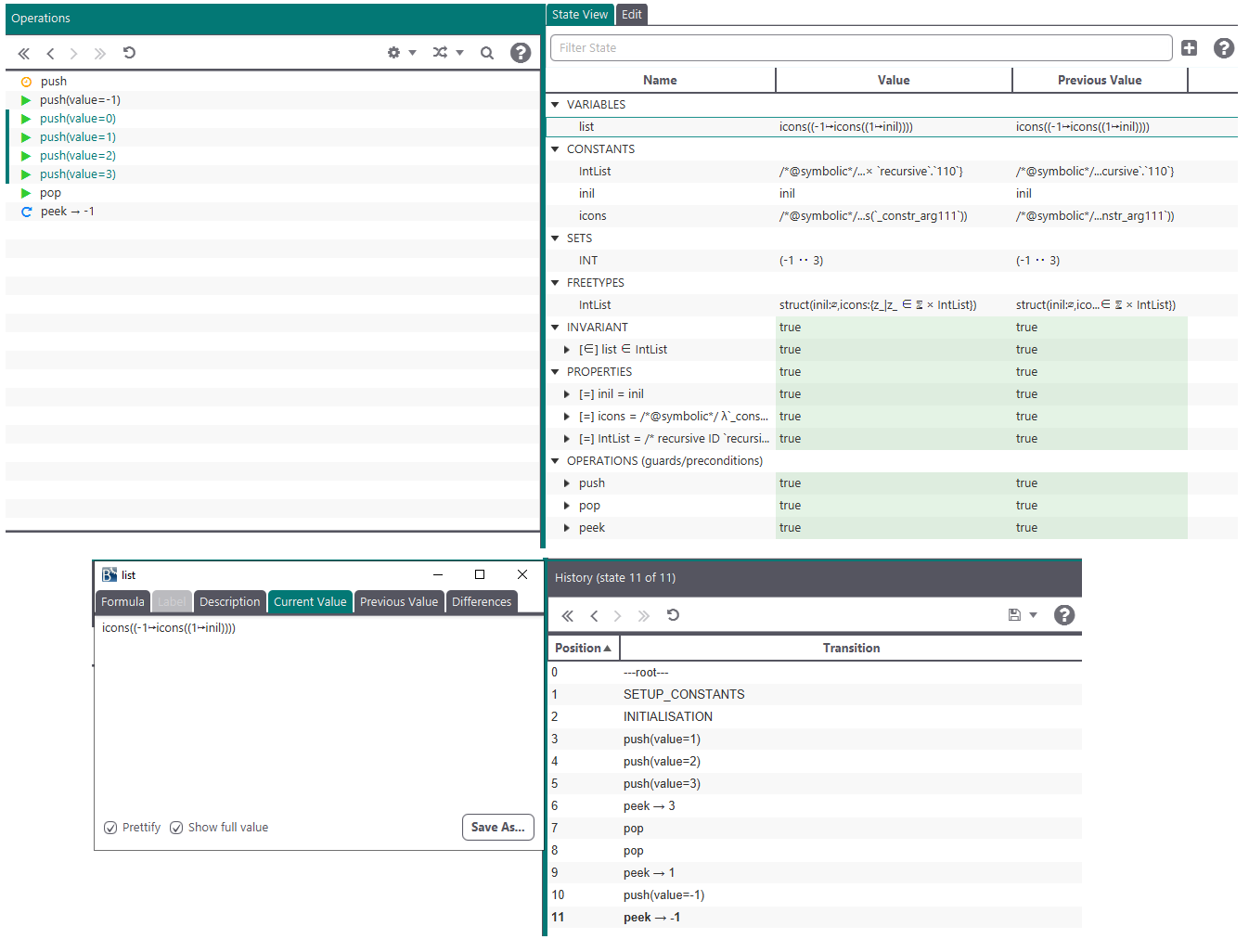
Here we implement a stack:
MACHINE IntListTest
FREETYPES IntList = inil, icons(INTEGER*IntList)
VARIABLES list
INVARIANT list : IntList
INITIALISATION list := inil
OPERATIONS
push(value) = PRE value : INTEGER THEN
list := icons(value, list)
END;
pop = PRE list /= inil THEN
list := prj2(icons~(list))
END;
value <-- peek = PRE list : ran(icons) THEN
value := prj1(icons~(list))
END
END
Example usage in ProB2-UI:
External Functions
As of version 1.3.5-beta7 ProB can make use of externally defined functions. These functions must currently be written in Prolog (in principle C, Java, Tcl or even other languages can be used via the SICStus Prolog external function interfaces). These functions can be used to write expression, predicates, or substitutions. The general mechanism that is used is to mark certain DEFINITIONS as external, in which case ProB will make use of external Prolog code rather than using the right-hand-side of the DEFINITION whenever it is used. However, these DEFINITIONS can often (unless they are polymorphic) be wrapped into B (constant) functions. If you just want to use the standard external functions already defined by ProB, then you don't have to understand this mechanism in detail (or at all).
We have a PDF describing the external functions generated from a ProB-Jupyter notebook: File:ExternalFunctions.pdf The Notebook is available and can now be launched via binder.
Standard Libraries provided by ProB
In a first instance we have predefined a series of external functions and grouped them in various library machines and definition files:
- LibraryMath.mch: defining sin, cos, tan, sinx, cosx, tanx, logx, gcd, msb, random as well as access to all other Prolog built-in arithmetic functions.
- LibraryStrings.mch: functions manipulating B STRING objects by providing length, append, split and conversion functions chars, codes.
- LibraryStrings.def used by LibraryStrings.mch: providing direct access to various operators on strings (STRING_LENGTH, STRING_APPEND, STRING_SPLIT INT_TO_STRING,...)
- LibraryFiles.mch: various functions to obtain information about files and directories in the underlying file system
- LibraryIO.def: providing functions to write information to screen or file. Note: these external functions are polymorphic and as such cannot be defined as B constants: you have to use the DEFINITIONS provided in LibraryIO.def.
- CHOOSE.def: providing the Hilbert choice operator for choosing a designated element from each set. Again, this function is polymorphic and thus cannot be defined as a B function. This function is useful for defining recursive functions over sets (see also TLA). Note that it in ProB it is undefined for the empty set.
- LibraryMeta.def: providing access to meta-information about the loaded model (PROJECT_INFO), about the state space (HISTORY, STATE_TRANS, ...) and about ProB itself (GET_PREF, PROB_INFO_STR, PROB_INFO_INT,..).
- LibraryReals.def: providing access to operators on Reals and Floats (RSIN, RCOS, RTAN, REXP, ROUND, RLOG,RSQRT,...).
- LibraryRegex.def: providing access to regular expression operators on strings (REGEX_MATCH, REGEX_REPLACE, REGEX_SEARCH,...)
- LibraryCSV.def: contains a READ_CSV external function to read in CSV files or strings and convert them to a B data structure
- LibrarySVG.def: providing utility functions for VisB (svg_points, svg_axis,...)
- LibraryXML.def: contains a READ_XML external function to read in XML files or strings and convert them to a B data structure with strings and records. Also contains READ_JSON_AS_XML/READ_JSON_FROM_STRING_AS_XML to read JSON files and converting them to the same B format.
- LibraryBits.def: contains bit-manipulation functions on integers (BNOT, BAND, BXOR,...).
- SORT.def: providing sorting related functions (SORT, SQUASH, REPLACE).
- SCCS.def: providing access to SCCS to compute the strongly connected components of a relation and CLOSURE1 an alternative algorithm for compting the transitive closure of a relation.
- LibraryJSON.def and LibraryJSON.mch providing the functions READ_JSON, READ_JSON_FROM_STRING, WRITE_JSON, WRITE_JSON_TO_STRING and the freetype JsonValue to read and write JSON data.
- LibraryZMQ_RPC.def and LibraryZMQ_RPC.mch: providing access to a JSON RPC (Remote Procedure Call) library either over regular sockets or ZMQ sockets. More information is available on JSON and Sockets.
Since version 1.5 the standard library is shipped with ProB and references to machines and DEFINITION-files in the standard library are resolved automatically when referenced (see PROBPATH for information about how to customize the lookup path).
To use a library machine you can use the SEES mechanism:
SEES LibraryMath
Note that for rules machines (.rmch) you have to use REFERENCES instead.
In general you can do the following with an external function, such as sin, wrapped into a constant:
- apply the function: sin(x)
- compute the image of the function: sin[1..100]
- compose the function with a finite relation on the left: ([1..100] ; sin)
- compute the domain of the function: dom(sin)
To use a library definition file, you need to include the file in the DEFINITIONS clause:
DEFINITIONS "LibraryIO.def"
Overview of the External Function DEFINITION Mechanism
Currently, external functions are linked to classical B machines using B DEFINITIONS as follows:
- one definition, which defines the function as it is seen by tools other than ProB (e.g., Atelier-B). Suppose we want to declare an external cosinus function named COS, then this definition could be COS(x) == cos(x).
- one definition declaring the type of the function. For COS this would be EXTERNAL_FUNCTION_COS == INTEGER --> INTEGER.
- Prolog code which gets called by ProB in place of the right-hand-side of the first definition
Usually, it is also a good idea to encapsulate the external function inside a CONSTANT which is defined as a lambda abstraction with as body simply the call to the first DEFINITION. For COS this would be cos = %x.(x:NATURAL|COS(x)). Observe that for Atelier-B this is a tautology. For ProB, the use of such a constant allows one to have a real B function representing the external function, for which we can compute the domain, range, etc.
For the typing of an external function NAME with type TYPE there are three possibilities, depending on whether the function is a function, a predicate or a substitution:
- EXTERNAL_FUNCTION_NAME == TYPE
- EXTERNAL_PREDICATE_NAME == TYPE
- EXTERNAL_SUBSTITUTION_NAME == TYPE
In case the external function is polymorphic, the DEFINITION can take extra arguments: each argument is treated like a type variable. For example, the following is used in CHOOSE.def to declare the Hilbert choice operator:
- EXTERNAL_FUNCTION_CHOOSE(T) == (POW(T)-->T)
Recursively Defined Functions
Symbolic Functions and Relations
Take the following function:
CONSTANTS parity
PROPERTIES
parity : (NATURAL --> {0,1}) &
parity(0) = 0 &
!x.(x:NATURAL => parity(x+1) = 1 - parity(x))
Here, ProB will complain that it cannot find a solution for parity. The reason is that parity is a function over an infinite domain, but ProB tries to represent the function as a finite set of maplets.
There are basically four solutions to this problem:
- Write a finite function:
parity : (NAT --> {0,1}) &
parity(0) = 0 &
!x.(x:NAT & x<MAXINT => parity(x+1) = 1 - parity(x))
- Rewrite your function so that in the forall you do not refer to values of parity greater than x:
parity : (NATURAL --> {0,1}) &
parity(0) = 0 &
!x.(x:NATURAL1 => parity(x) = 1 - parity(x-1))
- Write your function constructively using a single recursive equation using set comprehensions, lambda abstractions, finite sets and set union. This requires ProB 1.3.5-beta7 or higher and you need to declare parity as ABSTRACT_CONSTANT. Here is a possible equation:
parity : INTEGER <-> INTEGER &
parity = {0|->0} \/ %x.(x:NATURAL1|1-parity(x-1))
Note, you have to remove the check parity : (NATURAL --> {0,1}), as this will currently cause expansion of the recursive function. We describe this new scheme in more detail below.
- Another solution is try and write your function constructively and non-recursively, ideally using a lambda abstraction:
parity : (NATURAL --> INTEGER) & parity = %x.(x:NATURAL|x mod 2)
- Here ProB detects that parity is an infinite function and will keep it symbolic (if possible). With such an infinite function you can:
- apply the function, e.g., parity(10001) is the value 1
- compute the image of the function, e.g., parity[10..20] is {0,1}
- check if a tuple is a member of the function, e.g., 20|->0 : parity
- check if a tuple is not a member of the function, e.g., 21|->0 /: parity
- check if a finite set of tuples is a subset of the function, e.g., {20|->0, 120|->0, 121|->1, 1001|->1} <: parity
- check if a finite set of tuples is not a subset of the function, e.g., {20|->0, 120|->0, 121|->1, 1001|->2} /<: parity
- compose the function with a finite relation, e.g., (id(1..10) ; parity) gives the value [1,0,1,0,1,0,1,0,1,0]
- sometimes compute the domain of the function, here, dom(parity) is determined to be NATURAL. But this only works for simple infinite functions.
- sometimes check that you have a total function, e.g., parity: NATURAL --> INTEGER can be checked by ProB. However, if you change the range (say from INTEGER to 0..1), then ProB will try to expand the function.
- In version 1.3.7 we are adding more and more operators that can be treated symbolically. Thus you can now also compose two symbolic functions using relational composition ; or take the transitive closure (closure1) symbolically.
You can experiment with those by using the Eval console of ProB, experimenting for example with the following complete machine. Note, you should use ProB 1.3.5-beta2 or higher.
(You can also type expressions and predicates such as parity = %x.(x:NATURAL|x mod 2) & parity[1..10] = res directly into the online version of the Eval console).
MACHINE InfiniteParityFunction CONSTANTS parity PROPERTIES parity : NATURAL --> INTEGER & parity = %x.(x:NATURAL|x mod 2) VARIABLES c INVARIANT c: NATURAL INITIALISATION c:=0 OPERATIONS Inc = BEGIN c:=c+1 END; r <-- Parity = BEGIN r:= parity(c) END; r <-- ParityImage = BEGIN r:= parity[0..c] END; r <-- ParityHistory = BEGIN r:= (%i.(i:1..c+1|i-1) ; parity) END END
You may also want to look at the tutorial page on modeling infinite datatypes.
When does ProB treat a set comprehension or lambda abstraction symbolically ?
Currently there are four cases when ProB tries to keep a function such as f = %x.(PRED|E) symbolically rather than computing an explicit representation:
- the domain of the function is obviously infinite; this is the case for predicates such as x:NATURAL; in version 1.3.7-beta5 or later this has been considerably improved. Now ProB also keeps those lambda abstractions or set comprehensions symbolic where the constraint solver cannot reduce the domain of the parameters to a finite domain. As such, e.g., {x,y,z| x*x + y*y = z*z} or {x,y,z| z:seq(NATURAL) & x^y=z} are now automatically kept symbolic.
- f is declared to be an ABSTRACT_CONSTANT and the equation is part of the PROPERTIES with f on the left.
- the preference SYMBOLIC is set to true (e.g., using a DEFINITION SET_PREF_SYMBOLIC == TRUE)
- a pragma is used to mark the lambda abstraction as symbolic as follows: f = /*@ symbolic */ %x.(PRED|E); this requires ProB version 1.3.5-beta10 or higher. In Event-B, pragmas are represented as Rodin database attributes and one should use the symbolic constants plugin.
Recursive Function Definitions in ProB
As of version 1.3.5-beta7 ProB now accepts recursively defined functions. For this:
- the function has to be declared an ABSTRACT_CONSTANT.
- the function has to be defined using a single recursive equation with the name of the function on the left of the equation
- the right-hand side of the equation can make use of lambda abstractions, set comprehensions, set union and other finite sets
Here is a full example:
MACHINE Parity
ABSTRACT_CONSTANTS parity
PROPERTIES
parity : INTEGER <-> INTEGER &
parity = {0|->0} \/ %x.(x:NATURAL1|1-parity(x-1))
END
As of version 1.6.1 you can also use IF-THEN-ELSE and LET constructs in the body of a recursive function. The above example can for example now be written as:
MACHINE ParityIFTE ABSTRACT_CONSTANTS parity PROPERTIES parity : INTEGER <-> INTEGER & parity = %x.(x:NATURAL|IF x=0 THEN 0 ELSE 1-parity(x-1)END) END
Operations applicable for recursive functions
With such a recursive function you can:
- apply the function to a given argument, e.g., parity(100) will give you 0;
- compute the image of the function, e.g., parity[1..10] gives {0,1}.
- composing it with another function, notably finite sequences: ([1,2] ; parity) corresponds to the "map" construct of functional programming and results in the output [1,0].
Also, you have to be careful to avoid accidentally expanding these functions. For example, trying to check parity : INTEGER <-> INTEGER or parity : INTEGER +-> INTEGER will cause older version of ProB to try and expand the function. ProB 1.6.1 can actually check parity:NATURAL --> INTEGER, but it cannot check parity:NATURAL --> 0..1.
There are the following further restrictions:
- ProB does not support mutual recursion yet
- the function is not allowed to depend on other constants, unless those other constants can be valued in a deterministic way (i.e., ProB finds only one possible solution for them)
Memoization for Functions
As of version 1.9.0-beta9 ProB allows you to annotate functions in the ABSTRACT_CONSTANTS section for memoization. Memoization is a technique for storing results of function applications and reusing the result if possible to avoid re-computing the function for the same arguments again.
To enable memoization you either need to
- annotate the function in the ABSTRACT_CONSTANTS section with the pragma /*@desc memo */
- set the preference MEMOIZE_FUNCTIONS to true. In this case ProB will try to memoize all functions in the ABSTRACT_CONSTANTS section, unless they are obviously small and finite and can thus be precomputed completely.
Take the following example:
MACHINE MemoizationTests
ABSTRACT_CONSTANTS
fib /*@desc memo */,
fact /*@desc memo */
PROPERTIES
fib = %x.(x:NATURAL |
(IF x=0 or x=1 THEN 1
ELSE fib(x-1)+fib(x-2)
END))
&
fact = %x.(x:NATURAL|(IF x=0 THEN 1 ELSE x*fact(x-1) END))
ASSERTIONS
fib(30)=1346269;
fib[28..30] = {514229,832040,1346269};
30|->1346269 : fib;
30|->1346268 /: fib;
{x| 30|->x:fib} = {1346269};
END
Memoization means that the recursive Fibonacci function now runs in linear time rather than in exponential time. Generally, memoization is useful for functions which are complex to compute but which are called repeatedly with the same arguments.
As can be seen above, memoization is active for
- function calls such as fib(30) (which in turn calls fib(29) and fib(28) which are also memoized)
- computation of relational image such as fib[28..30], which internally results in three function calls to fib
- membership predicates of the form x|->y:fib, where x is a known value
- non-membership predicates of the form x|->y/:fib, where x is a known value
The following points are relevant:
- Memoization is currently only possible for functions declared in the ABSTRACT_CONSTANTS section
- Memoization means that all results of function calls are stored. The memoization table is reset when another B machine is loaded or the same B machine is re-loaded.
- Memoized functions are often treated in a similar way to symbolic functions. If your function is finite and relatively small, it may be better to put the function into the CONCRETE_CONSTANTS section so that it gets computed in its entirety once.
- Memoization of a function f is currently not active for computations such as dom(f).
- If a predicate requires the computation of the full function, e.g., ran(f), then the results will be stored and will be available for future function calls or in case the full value is needed again.
With the command-line version probcli you can use the -profile command to obtain some statistics about memoization. An example output is the following one:
-------------------------- ProB profile info after 9670 ms walltime (7217 ms runtime) No source profiling information available Recompile ProB with -Dprob_src_profile=true No profiling information available Recompile ProB with -Dprob_profile=true MEMO Table: Summary of reuse per memoization ID: MemoID 1 (prime) : Values Stored: 999 (? ms to compute), Reused ? MemoID 2 (fib) : Values Stored: 31 (? ms to compute), Reused ? MemoID 3 (fact) : Values Stored: 11 (? ms to compute), Reused ? MemoID 4 (evenupto) : Values Stored: 0 (? ms to compute), Reused ? MemoID 5 (sum) : Values Stored: 1001 (? ms to compute), Reused ? MemoID 6 (M91) : Values Stored: 111 (? ms to compute), Reused ? Hashes computed: 1002, expansions reused: 0 Memoization functions registered: 6, results reused: 1345
If the compile time flag -Dprob_profile=true is set, the output is more detailed:
... MEMO Table: Summary of reuse per memoization ID: MemoID 1 (prime) : Values Stored: 999 (336 ms to compute), Reused 1003 MemoID 2 (fib) : Values Stored: 31 (20 ms to compute), Reused 45 MemoID 3 (fact) : Values Stored: 11 (10 ms to compute), Reused 1 MemoID 4 (evenupto) : Values Stored: 0 (0 ms to compute), Reused 0 MemoID 5 (sum) : Values Stored: 1001 (16659 ms to compute), Reused 1 MemoID 6 (M91) : Values Stored: 111 (15 ms to compute), Reused 295 Hashes computed: 1002, expansions reused: 0 Memoization functions registered: 6, results reused: 1345
In verbose mode (-v flag for probcli) you also obtain information about individual stored results.
MEMO Table:
MemoID 1 stored FUNCTION prime
: %x.(x : NATURAL|(IF !y.(y : 2 .. x - 1 => x mod y /= 0) THEN TRUE ELSE FALSE END))
MemoID 2 stored FUNCTION fib
: %x.(x : NATURAL|(IF x : {0,1} THEN 1 ELSE MEMOIZE_STORED_FUNCTION(2)(x - 1) + MEMOIZE_STORED_FUNCTION(2)(x - 2) END))
...
MemoID 6 stored FUNCTION M91
: %x.(x : INTEGER|(IF x > 100 THEN x - 10 ELSE MEMOIZE_STORED_FUNCTION(6)(MEMOIZE_STORED_FUNCTION(6)(x + 11)) END))
MemoID 1 (prime) result for argument 13
: TRUE
MemoID 1 (prime) result for argument 14
: FALSE
MemoID 1 (prime) result for argument 2
: TRUE
MemoID 1 (prime) result for argument 3
: TRUE
...
Memoization functions registered: 6, results reused: 1345
Tips: B Idioms
Also have a look at Tips:_Writing_Models_for_ProB.
Let
Classical B only has a LET substitution, no let construct for predicates or expressions. Event-B has no let construct whatsoever.
ProB's Extended Syntax
Since version 1.6.1-beta (28th of April 2016), ProB supports the use of the LET substitution syntax in expressions and predicates.
Examples:
>>> LET a BE a = 10 IN a + 10 END Expression Value = 20
>>> LET a BE a=10 IN a END + 10 Expression Value = 20
>>> LET a BE a=10 IN a END = 10 Predicate is TRUE
>>> LET a BE a = 10 IN a < 10 END Predicate is FALSE
>>> LET a BE a=10 IN a /= 10 END or 1=1 Predicate is TRUE
>>> LET a, b BE a = 10 & b = 1 IN a + b END Expression Value = 11
Let for predicates
For predicates this encodes a let predicate:
#x.(x=E & P)
corresponds to something like
let x=E in P
Within set comprehensions one can use the following construct:
dom({x,y|y=E & P})
corresponds to something like
{x|let y=E in P}
One can also use the ran operator or introduce multiple lets in one go:
dom(dom({x,y,z|y=E1 & z=E2 &P}))
or
ran({y,z,x|y=E1 & z=E2 &P})
both encode
{x|let y=E1 & z=E2 in P}
Let for expressions
In case F is a set expression, then the following construct can be used to encode a let statement:
UNION(x).(x=E|F)
corresponds to something like
let x=E in F
The following construct has exactly the same effect:
INTER(x).(x=E|F)
If-Then-Else
Classical B only has an IF-THEN-ELSE substitution (aka statement), no such construct for predicates or expressions.
Nightly Builds
Since version 1.6.1-beta (28th of April 2016), ProB supports the use of the LET substitution syntax in expressions and predicates.
Examples:
>>> IF 1 = 1 THEN 3 ELSE 4 END Expression Value = 3
>>> IF 1 = 1 THEN 3 ELSE 4 END + 5 Expression Value = 8
>>> IF 1=1 THEN TRUE = FALSE ELSE TRUE=TRUE END Predicate is FALSE
>>> IF 1=1 THEN TRUE = FALSE ELSE TRUE=TRUE END or 1=1 Predicate is TRUE
Expressions
The following construct
%((x).(x=0 & PRED|C1)\/%(x).(x=0 & not(PRED)|C2)) (0)
encodes an if-then-else for expressions:
IF PRED THEN C1 ELSE C2 END
The former lambda-construct is recognised by ProB and replaced internally by an if-then-else construct. The latter syntax is actually now recognised as well by ProB 1.6 (version 1.6.0 still requires parentheses around the IF-THEN-ELSE; version 1.6.1 no longer requires them).
finite
In classical B there is no counterpart to the Event-B finite operator. However, the following construct has the same effect as finite(x) (and is recognised by ProB):
x : FIN(x)
all-different
One can encode the fact that n objects x1,...,xn are pair-wise different using the following construct (recognised by ProB):
card({x1,...,xn})=n
map
Given a function f and a sequence sqce one can map the function over all elements of sqce using the relational composition operator ;:
(sqce ; f)
For example, ([1,2,3] ; succ) gives us the sequence [2,3,4].
Recursion using closure1
Even though B has no built-in support for recursion, one can use the transitive closure operator closure1 to compute certain recursive functions. For this we need to encode the recursion as a step function of the form:
%(in,acc).(P|(inr,accr))
where P is a predicate which in case we have not yet reached a base case for the input value in. The computation result has to be stored in an accumulator: acc is the accumulator before the recursion step, accr after. inr is the new input value for the recursive call. In case the base case is reached for in, the predicate P should be false and the value of the recursive call should be the value of the accumulator.
The value of the recursive function can thus be obtained by calling:
closure1(step)[{(in,ia)}](b)
where in is the input value, b is the base case and ia is the initial (empty) accumulator.
For example, to sort a set of integers into a ascending sequence, we would define the step function as follows:
step = %(s,o).(s/={} | (s\{min(s)},o<-min(s)))
A particular call would be:
closure1(step)[{({4,5,2},[])}]({})
resulting in the sequence [2,4,5].
Observe that, even though closure1(step) is an infinite relation, ProB can compute the relational image of closure1(step) for a particular set such as {({4,5,2},[])} (provided the recursion terminates).
Recursion using ABSTRACT_CONSTANTS
Recursive functions can be declared using the ABSTRACT_CONSTANTS section in B machines. Functions declared as ABSTRACT_CONSTANTS are treated symbolically by ProB and not evaluated eagerly.
For example, to sort a set of integers into a ascending sequence, as above, we would define a recursive function as follows:
ABSTRACT_CONSTANTS
Recursive_Sort
PROPERTIES
Recursive_Sort : POW(INTEGER) <-> POW(INTEGER*INTEGER)
& Recursive_Sort =
%in.(in : POW(INTEGER) & in = {} | [])
\/ %in.(in : POW(INTEGER) & in /= {}
| min(in) -> Recursive_Sort(in\{min(in)}))
By defining Recursive_Sort as an abstract constant we indicate that ProB should handle the function symbolically, i.e. ProB will not try to enumerate all elements of the function. The recursive function itself is composed of two single functions: a function defining the base case and a function defining the recursive case. Note, that the intersection of the domains of these function is empty, and hence, the union is still a function.
Tips: Writing Models for ProB
The most common issue is that ProB needs to find values for the constants which satisfy the properties (aka axioms in Event-B). You should read the tutorial pages on this (in particular Understanding the ProB Setup Phases and Tutorial Troubleshooting the Setup)
- Try to use ProB as early as possible in the modeling process; this will make it easier to identify the cause of problems (and also will hopefully give you valuable feedback on your model as well).
- Try to put complicated properties into ASSERTIONS rather than PROPERTIES. Something like !s.(s<:S => P) will have to check P for all subsets of S (i.e., checking is exponential in the size of S)
- You may wish to give explicit values to certain constants. For example, in Event-B, this can be done by refining a context.
- Try to set the symbolic preference of ProB to true (use -p SYMBOLIC TRUE for probcli or set the Animation preference "Lazy expansion ... (SYMBOLIC)" to true) if you have large or infinite functions (see discussion about closure below). In symbolic mode, ProB will keep lambda expressions and set comprehensions symbolic as much as possible. In classical B, any ABSTRACT_CONSTANT will also at first be kept symbolic. However, there are only limited things you can do with a "symbolic" function without forcing an expansion: taking the value of a function is fine, computing the image over a set is also possible as is taking the union with another symbolic function.
Effective Constraint Solving with ProB
Existential Quantifiers
Existential quantifiers can pose subtle problems when solving constraint problems.
For an existential quantifier #x.P ProB will often wait until all variables in P apart from x are known to evaluate the quantifier. Indeed, if all variables apart from x are known, ProB can stop when it finds one solution for x. Take for example:
#x.(x:0..1000 & x=p) & p:101..104
Here, ProB will wait until p is known (e.g., 101) before enumerating possible values for x. However, it could be that the predicate P is required to instantiate the outside variable, as in this example:
#x.(x:100..101 & x=p) & p:NATURAL
Here, the existential quantifier is required to narrow down the possible values of p. Thus, before enumerating an unbounded variable, ProB will start enumerating the existential variable x. Note, however, that the priority with which it will be enumerated is much lower than if it was a regular variable! Hence:
- Tip: Beware of putting important domain variables into existential quantifiers.
One exception to the above treatment are existential quantifiers of the form #x.(x=E & P). They are recognised by ProB as LET-PREDICATES. This is a good use of the existential quantifier. This quantifier will never "block".
- Tip: use existential quantifiers as LET-PREDICATES #x.(x=E & P) to avoid repeated computations (common-subexpression elimination) and to make your predicates more readable
Universal Quantifiers
The situation is very similar to the existential quantifier. In the worst case ProB may delay evaluating a universal quantifier !x.(P=>Q) until all variables in P are known so as to be able to determine all values of x for which Q has to be checked.
There are a few optimisations:
- if ProB can determine that the domain of x is finite and small, then the universal quantifier will be expanded into a conjunction. E.g., !x.(x:1..3 & x<y => P(x) will be expanded into (1<y => P(1)) & (2<y => P(2)) & (3<y => P(3)) even if y is not yet known. Setting the preference SMT to true will increase the threshold for which this expansion occurs.
- if the quantifier is of the form !x.(x:S => P), then P will be gradually checked for every new value that is added to S; ProB does not wait for S to be completely known before checking the quantifier.
Tip: sometimes one can force expansion of a quantifier by using two implications. E.g., suppose we know that the domain of s is a subset of 1..10, then we can rewrite !x.(s(x)=5 => P(x) into !x.(x:1..10 => (s(x)=5 => P(x)). This will ensure that the quantifier is checked
Transitive Closure in Event-B
Classical B contains the transitive closure operator closure1. It is not available by default in Event-B, and axiomatisations of it may be very difficult to treat by ProB. Indeed, if you define the transitive closure in Event-B as a function tclos from relations to relations, ProB will try to find a value for tclos. The search space for this function is (2^n*n)^(2^n*n), where n is the size of the base set (see Tutorial Understanding the Complexity of B Animation). For n=3 this is already way too big too handle (the search space has 1.40e+1387 relations).
Hence, in Event-B, you should use a theory of the transitive closure which contains a special mapping file which instructs ProB to use the classical B operator. See the page on supporting Event-B theories along with the links to theories that can be used efficiently with ProB.
- Tip: within set comprehensions use the form dom({x,y|P}) rather than {x|#y.P}. This is generally more efficient.
Debugging
There are various ways in which you can debug your model. We focus here on debugging performance issues
Debugging with LibraryIO
The standard library "LibraryIO.def" contains various external functions and predicates with which you can instrument your formal model.
To use the library in your model you need to include the following
DEFINITIONS "LibraryIO.def"
With the external predicate printf you can view values of variables and identifiers. The printf predicate is always true and will print its arguments when all of them have been fully computed. The printf predicate uses the format from SICStus Prolog for the format string. The most important are ~w for printing an argument and ~n for a newline. There must be exactly as many ~w in the format string as there are aguments. Below is a small example, to inspect in which order ProB enumerates values. The example is typed in the REPL of probcli (started using the command probcli -repl File.mch where File.mch includes the definitions section above):
>>> {x,y | x:1..5 & y:1..2 & x+y=6 & printf("x=~w~n",[x]) & printf("y=~w~n",[y])}
y=1
x=5
y=2
x=4
Expression Value =
{(4|->2),(5|->1)}
As you can see, ProB has enumerated y before x, as its domain was smaller.
You can use the external function observe to inspect a list of identifiers:
>>> {x,y | x:1..5 & y:1..2 & x+y=6 & observe((x,y))}
observing x
observing y
y = 1 (walltime: 562188 ms)
. x = 5 (walltime: 562188 ms)
..* Value complete: x |-> y = (5|->1) (walltime: 562188 ms)
------
y = 2 (walltime: 562188 ms)
. x = 4 (walltime: 562188 ms)
..* Value complete: x |-> y = (4|->2) (walltime: 562188 ms)
------
Expression Value =
{(4|->2),(5|->1)}
With the external function TIME you can get the current time in seconds:
>>> TIME("sec")
Expression Value =
11
>>> TIME("now")
Expression Value =
1581432376
>>> TIME("now")
Expression Value =
1581432377
With the external function DELTA_WALLTIME you can get the time in milliseconds since the last call to DELTA_WALLTIME.
Performance Messages
By setting the preference PERFORMANCE_INFO to TRUE ProB will print various performance messages. For example it may print messages when the evaluation of comprehension sets has exceeded a threshold. This threshold (in ms) can be influenced by setting the preference PERFORMANCE_INFO_LIMIT.
Debugging Constants Setup
TRACE_INFO preference
By setting the preference TRACE_INFO to TRUE ProB will print additional messages when evaluating certain predicates, in particular the PROPERTIES clause of a B machine. With this feature you can observe how constants get bound to values and can sometimes spot expensive predicates and large values. Some additional information about debugging the PROPERTIES can be found in the Tutorial Troubleshooting the Setup. The preference also helps debugging the INITIALISATION clause of a B machine.
Let us take the following machine
MACHINE Debug CONSTANTS a,b,c PROPERTIES a = card(b) & b = %x.(x:1..c|x*x) & c : 1000..1001 & c < 1001 VARIABLES x INVARIANT x:NATURAL INITIALISATION x:=2 OPERATIONS Sqr = SELECT x:dom(b) THEN x := b(x) END; Finished = SELECT x /: dom(b) THEN skip END END
Here is how we can debug the constants setup using the TRACE_INFO preference:
$ probcli Debug.mch -p TRACE_INFO TRUE -init
% unused_constants(2,[a,c])
nr_of_components(1)
====> (1) c < 1001
====> (1) a = card(b)
====> (1) b = %x.(x : 1 .. c|x * x)
====> (1) c : 1000 .. 1001
finished_processing_component_predicates
grounding_wait_flags
:?: a int(?:0..sup)
:?: b VARIABLE: _31319 : GRVAL-CHECK
:?: c int(?:inf..1000)
--1-->> a
int(1000)
--1-->> b
AVL.size=1000
--1-->> c
int(1000)
% Runtime for SOLUTION for SETUP_CONSTANTS: 107 ms (walltime: 110 ms)
% Runtime to FINALISE SETUP_CONSTANTS: 0 ms (walltime: 0 ms)
=INIT=> x := 2
[=OK= 0 ms]
Profiling Constants Computation Time
ProB now also supports profiling the computation of constants defined by equations in the PROPERTIES, when profiling is active (see section below). The profiling can be achieved using the following table command -csv prob_constants_profile_info FILE:
probsli DebugSymbolicConstants.mch -csv prob_constants_profile_info user_output -init -p PROFILING_INFO TRUE -p PERFORMANCE_INFO TRUE % Runtime for SOLUTION for SETUP_CONSTANTS: 22 ms (walltime: 22 ms) % Runtime to FINALISE SETUP_CONSTANTS: 0 ms (walltime: 0 ms) Calling table command prob_constants_profile_info Constant Kind @desc Computation Runtime (ms) Computation Walltime (ms) Propagation Walltime (ms) # Calls Other Infos Valued Det.Value Instantiates c1 concrete 20 20 0 1 [] yes AVL-Set:10000 [] c2 concrete 2 2 0 1 [] yes AVL-Set:100 [] c3 concrete 0 0 0 1 [] yes AVL-Set:100 [] a3 abstract 0 0 0 1 [] yes SYMBOLIC-Set [] a2 abstract 0 0 0 1 [] yes SYMBOLIC-Set [] a1 abstract 0 0 0 1 [] yes SYMBOLIC-Set [] Finished exporting prob_constants_profile_info to user_output
In ProB Tcl/Tk this is available in the Debug -> Statistics menu, while in ProB2-UI it is available in the Graph and Table visualisation dialog. In probcli you can obtain a list of all available commands (callable via -csv CMD FILE) using probcli --help.
Debugging Constant Size
Indeed, for performance it can be much more efficient to expand a value (such as a function or relation) once, rather than keeping it symbolic. On the other, expanding a very large set can be costly in terms of memory. A useful feature to analyse these issues is the constants_analysis command. It generates a CSV table which can be inspected in an editor or a spreadsheet program. The table provides an overview of the constants, in particular their size and whether they are kept symbolic or expanded.
Note that B distinguishes between abstract and concrete constants. By default, concrete constants will be evaluated (unless they are known to be infinite or larger or annotated as symbolic). Abstract constants are more often kept symbolic. You can influence ProB's treatmen of constants by - choosing to put constants into the ABSTRACT_CONSTANTS or CONCRETE_CONSTANTS section - annotating the values with the /*@ symbolic */ pragma - annotating the constant with the /@ desc expand */ pragma to force expansion - annotating the constant with the /@desc memo */ pragma to memoize its evaluation (i.e., cache evaluation results involving the constant)
Let us examine this machine, where the constants a1,a2,a3 are identical to c1,c2,c3 but are located in the abstract rather than the concrete constants section:
MACHINE DebugSymbolicConstants
ABSTRACT_CONSTANTS
a1, a2, a3
CONCRETE_CONSTANTS
c1, c2, c3
PROPERTIES
a1 = %x.(x:1..10000|x+x) &
a2 = {x | x:1..10000 & x mod 100 = 0} &
a3 = %x.(x:1..100|x*x) &
c1 = %x.(x:1..10000|x+x) &
c2 = {x | x:1..10000 & x mod 100 = 0} &
c3 = %x.(x:1..100|x*x)
END
The command can now be run as follows. Here the output is written to the console (by providing user_output as file name). The list of constants is sorted according to size.
probcli DebugSymbolicConstants.mch -init -csv constants_analysis user_output
...
Calling table command constants_analysis
! Message (source: constants_analysis):
! Abstract constant is stored symbolically but can be expanded to a finite set of size 10000 (by moving to ABSTRACT_CONSTANTS or annotating with /*@desc expand */ pragma): a1
! Line: 3 Column: 2 until Line: 3 Column: 4 in file: /Users/leuschel/git_root/prob_examples/public_examples/B/Tester/ConstantsDebug/DebugSymbolicConstants.mch
! Message (source: constants_analysis):
! Abstract constant is stored symbolically but can be expanded to a finite set of size 100 (by moving to ABSTRACT_CONSTANTS or annotating with /*@desc expand */ pragma): a2
! Line: 3 Column: 6 until Line: 3 Column: 8 in file: /Users/leuschel/git_root/prob_examples/public_examples/B/Tester/ConstantsDebug/DebugSymbolicConstants.mch
! Message (source: constants_analysis):
! Abstract constant is stored symbolically but can be expanded to a finite set of size 100 (by moving to ABSTRACT_CONSTANTS or annotating with /*@desc expand */ pragma): a3
! Line: 3 Column: 10 until Line: 3 Column: 12 in file: /Users/leuschel/git_root/prob_examples/public_examples/B/Tester/ConstantsDebug/DebugSymbolicConstants.mch
CONSTANT class kind termsize value
c1 CONCRETE AVL-Set:10000 90002 #10000:{(1|->2),(2|->4),...,(9999|->19998),(10000|->20000)}
c3 CONCRETE AVL-Set:100 902 {(1|->1),(2|->4),(3|->9),(4|->16),(5|->25),(6|->36),(7|->49),(8|->64),(9|->81),(10|->100),(11|->121)...
a3 ABSTRACT FINITE-SYMBOLIC-Set:100 708 /*@symbolic*/ %x.(x : {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29...
c2 CONCRETE AVL-Set:100 602 {100,200,300,400,500,600,700,800,900,1000,1100,1200,1300,1400,1500,1600,1700,1800,1900,2000,2100,220...
a2 ABSTRACT FINITE-SYMBOLIC-Set:100 162 /*@symbolic*/ {x|x : (1 .. 10000) & x mod 100 = 0}
a1 ABSTRACT FINITE-SYMBOLIC-Set:10000 151 /*@symbolic*/ %x.(x : (1 .. 10000)|x + x)
Finished exporting constants_analysis to user_output
Let us now add pragmas to study their influence:
MACHINE DebugSymbolicConstants_pragmas
ABSTRACT_CONSTANTS
a1 /*@desc expand*/, a2 /*@desc expand*/, a3 /*@desc expand*/
CONCRETE_CONSTANTS
c1 /*@desc memo */, c2, c3
PROPERTIES
a1 = %x.(x:1..10000|x+x) &
a2 = {x | x:1..10000 & x mod 100 = 0} &
a3 = %x.(x:1..100|x*x) &
c1 = /*@symbolic */ %x.(x:1..10000|x+x) &
c2 = /*@symbolic */ {x | x:1..10000 & x mod 100 = 0} &
c3 = /*@symbolic */ %x.(x:1..100|x*x)
END
You can see that a1,a2 and a3 are expanded, while c1, c2 and c3 kept symbolic.
probcli DebugSymbolicConstants_pragmas.mch -init -csv constants_analysis user_output
...
Calling table command constants_analysis
! Message (source: constants_analysis):
! Concrete constant is stored symbolically but can be expanded to a finite set of size 10000 (by annotating with /*@desc expand */ pragma): c1
! Line: 5 Column: 2 until Line: 5 Column: 4 in file: /Users/leuschel/git_root/prob_examples/public_examples/B/Tester/ConstantsDebug/DebugSymbolicConstants_pragmas.mch
! Message (source: constants_analysis):
! Concrete constant is stored symbolically but can be expanded to a finite set of size 100 (by annotating with /*@desc expand */ pragma): c2
! Line: 5 Column: 22 until Line: 5 Column: 24 in file: /Users/leuschel/git_root/prob_examples/public_examples/B/Tester/ConstantsDebug/DebugSymbolicConstants_pragmas.mch
! Message (source: constants_analysis):
! Concrete constant is stored symbolically but can be expanded to a finite set of size 100 (by annotating with /*@desc expand */ pragma): c3
! Line: 5 Column: 26 until Line: 5 Column: 28 in file: /Users/leuschel/git_root/prob_examples/public_examples/B/Tester/ConstantsDebug/DebugSymbolicConstants_pragmas.mch
CONSTANT class kind termsize value
a1 ABSTRACT AVL-Set:10000 90002 #10000:{(1|->2),(2|->4),...,(9999|->19998),(10000|->20000)}
a3 ABSTRACT AVL-Set:100 902 {(1|->1),(2|->4),(3|->9),(4|->16),(5|->25),(6|->36),(7|->49),(8|->64),(9|->81),(10|->100),(11|->121)...
c3 CONCRETE FINITE-SYMBOLIC-Set:100 708 /*@symbolic*/ %x.(x : {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29...
a2 ABSTRACT AVL-Set:100 602 {100,200,300,400,500,600,700,800,900,1000,1100,1200,1300,1400,1500,1600,1700,1800,1900,2000,2100,220...
c2 CONCRETE FINITE-SYMBOLIC-Set:100 162 /*@symbolic*/ {x|x : (1 .. 10000) & x mod 100 = 0}
c1 MEMOIZED FINITE-SYMBOLIC-Set:10000 154 /*@symbolic*/ %x.(x : (1 .. 10000)|x + x)
Finished exporting constants_analysis to user_output
For symbolic constants you can also inspect the value graphically. Using probcli this can be done as follows:
probcli -init DebugSymbolicConstants_pragmas.mch -dot_expr id_value_formula_tree c3 c3.pdf
The command is also available by right-clicking on an identifier in the Evaluation View of ProB Tcl/Tk.
Finding Constant Expressions
Using the command
-csv constant_expr_analysis FILE
you can detect possibly expensive constant expressions used in operation bodies.
It could be interesting to extract these expressions out of operations (e.g., into a constant or variable computed after initialisation), to avoid repeated re-computation of the expression.
Note, this command is also carried out as part of the -lint command. You can also execute -lint_operations, which will not generate a CSV table.
Debugging Animation or Execution
By using the -animate_stats flag, you can see execution times for operations that are executed either using the -execute or -animate commands. In verbose mode (-v flag) you also see the memory consumption.
$ probcli Debug.mch -execute_all -animate_stats
% unused_constants(2,[a,c])
% Runtime for SOLUTION for SETUP_CONSTANTS: 79 ms (walltime: 80 ms)
1 : SETUP_CONSTANTS
91 ms walltime (89 ms runtime), since start: 1107 ms
2 : INITIALISATION
5 ms walltime (4 ms runtime), since start: 1112 ms
3 : Sqr
10 ms walltime (10 ms runtime), since start: 1123 ms
4 : Sqr
0 ms walltime (0 ms runtime), since start: 1123 ms
5 : Sqr
1 ms walltime (0 ms runtime), since start: 1124 ms
6 : Sqr
0 ms walltime (0 ms runtime), since start: 1124 ms
7 : Finished
3 ms walltime (4 ms runtime), since start: 1127 ms
Infinite loop reached after 8 steps (looping on Finished).
% Runtime for -execute: 116 ms (with gc: 116 ms, walltime: 119 ms); time since start: 1132 ms
Profiling
You can obtain some profiling information using the -prob_profile command. This command unfortunately requires that ProB was compiled using special flags (-Dprob_profile=true and -Dprob_src_profile=true). As of version 1.13.1-nightly September 2024, the profiling can be enabled by setting the preference PROFILING_INFO to TRUE (simply add -p PROFILING_INFO TRUE to the invocation below):
$ probcli ../prob_examples/public_examples/B/Tutorial/Debug.mch -execute_all -prob_profile -p PROFILING_INFO TRUE % unused_constants(2,[a,c]) % Runtime for SOLUTION for SETUP_CONSTANTS: 2 ms (walltime: 2 ms) Infinite loop reached after 8 steps (looping on Finished). % Runtime for -execute: 3 ms (with gc: 3 ms, walltime: 3 ms); since start: 0 sec 426 ms -------------------------- PROB PROFILING INFORMATION after 426 ms walltime (268 ms runtime) 168.843 MB No source profiling information available Set preference SOURCE_PROFILING_INFO to TRUE ---- ProB Runtime Profiler ---- ---- Time spent in B operations and invariant evaluation Operation : Total Runtime ms (Total ms walltime & Minimum - Maximum ms walltime; #calls Number of Calls) $setup_constants : 2 ms (2 ms walltime & 2 - 2 ms walltime; #calls 1) INVARIANT : 1 ms (0 ms walltime & 0 - 0 ms walltime; #calls 7) Finished : 0 ms (1 ms walltime & 1 - 1 ms walltime; #calls 1) Sqr : 0 ms (0 ms walltime & 0 - 0 ms walltime; #calls 5) $initialise_machine : 0 ms (0 ms walltime & 0 - 0 ms walltime; #calls 1) Total Walltime: 3 ms for #calls 15 ---- Time spent evaluating CONSTANTS (defined by equations) Operation : Total Runtime ms (Total ms walltime & Minimum - Maximum ms walltime; #calls Number of Calls) Total Walltime: 0 ms for #calls 0 Stored 0 AVL sets for state compression
Note, if you memoize functions you can also inspect time spent in evaluating function calls. E.g., if you set the preference MEMOIZE_FUNCTIONS to true then all abstract constants will be memoised and you can inspect number of calls and time. See Memoization_for_Functions.
Exporting Profile to CSV
You can also export the profile information into a CSV file (or on the console when providing "user_output" as special file name):
$ probcli ../prob_examples/public_examples/B/Tutorial/Debug.mch -execute_all -csv prob_profile_info user_output -p PROFILING_INFO TRUE % unused_constants(2,[a,c]) % Runtime for SOLUTION for SETUP_CONSTANTS: 3 ms (walltime: 2 ms) Infinite loop reached after 8 steps (looping on Finished). % Runtime for -execute: 3 ms (with gc: 3 ms, walltime: 3 ms); since start: 0 sec 430 ms Calling table command prob_profile_info Operation/Action Total Runtime (ms) Total Walltime (ms) # Calls Max. Walltime (ms) Max. Witness ID Min. Walltime (ms) $setup_constants 3 2 1 2 unknown 2 Sqr 0 1 5 1 unknown 0 INVARIANT 0 0 7 0 unknown 0 Finished 0 0 1 0 unknown 0 $initialise_machine 0 0 1 0 unknown 0 Finished exporting prob_profile_info to user_output
Profiling External Function Calls
You can also generate a profile of the external functions called. Take for example this machine:
MACHINE TestLibraryHash
DEFINITIONS
"LibraryHash.def"
ASSERTIONS
HASH(2+2) = HASH(4);
SHA_HASH(2**10) = SHA_HASH(1024);
SHA_HASH(2**10) /= SHA_HASH({1024});
SHA_HASH({2,3,1,4,5}) = SHA_HASH(1..5);
SHA_HASH({2,3,1,4,5}*{TRUE}) = SHA_HASH({x,y|x:1..5 & (y=TRUE <=> x<6)});
SHA_HASH({2,3,1,4,5}) /= SHA_HASH({2,3,1,4});
SHA_HASH_HEX({2,3,1,4,5}) = SHA_HASH_HEX(1..5);
SHA_HASH_HEX({2,3,1,4,5}) /= SHA_HASH_HEX({2,3,1,4})
END
The -prob-profile command above will also print out information about calls to external functions. This command generates a CSV table of the called external functions; instead of user_output you should provide the name of a file:
probcli TestLibraryHash.mch -init -repl -csv prob_external_fun_profile_info user_output -assertions -p PROFILING_INFO TRUE ... Calling table command prob_external_fun_profile_info Operation/Action Total Runtime (ms) Total Walltime (ms) # Calls Max. Walltime (ms) Max. Witness ID Min. Walltime (ms) SHA_HASH 0 1 16 1 unknown 0 SHA_HASH_HEX 0 0 8 0 unknown 0 Finished exporting prob_external_fun_profile_info to user_output