Bash Completion

For the Bash Unix Shell we provide command completion support.

Example

$ probcli -re<TAB>
    -refchk  -repl

Installation

A generated version of the command completion for Bash is available here. To install download the linked file and store it locally on your machine. To enable the completion you need to source the file.

$ source <path to prob_completion.sh>

To enable the completion automatically add the line above to your Bash settings, e.g. in the .bashrc or .profile files in your home directory.

Contributing

The source code can be found on our GitLab. Bugs and improvements can be submitted on our GitHub issue tracker.

Common Subexpression Elimination 

As of version 1.5.1 ProB supports common subexpression elimination (CSE).

Basics of CSE

To enable CSE you need to set the advanced preference CSE to true (this can be done using the switch -p CSE TRUE when using the command-line version probcli or using the Advanced Preferences command in ProB Tcl/Tk). With CSE enabled, ProB will translate the predicate

x:dom(f(a)) & r=f(a)(x)

into

(LET @0==(f(a)) IN x ∈ dom(@0) ∧ r = @0(x))

before evaluating it. As you can see, the common sub-expression f(a) has been lifted into a LET statement. This has the advantage that the expression f(a) will only get evaluated once (rather than twice, in case x:dom(f(a))). Identifiers introduced by the CSE always start with the @-sign. As another example, the predicate

x*x+2*x > y*y*y & y*y*y > x*x+2*x

gets translated into

LET @2==(x*x+2*x) IN (LET @4==((y*y)*y) IN @2 > @4 & @4 > @2))

You may observe that the B-language does not have a let-construct for expression nor predicates (only for substitutions). There are various ways one can overcome this (e.g., using an existential quantifier for a predicate), but ProB adds its own LET-construct to the language in the interpreter. Moreover, to avoid issues with well-definedness and ensuring that ProB only evaluates the LET expressions when really needed, this LET has a different behaviour than the "standard" constructs. Indeed, ProB's LET is lazy, i.e., it will only evaluate the expression when required by the computation of the body of the LET. For example, in

LET @1==f(a) IN 2>3 & @1+@1>10

the expression f(a) will never be evaluated. This is important for well-definedness (e.g., suppose a is not in the domain of f) and for performance.

Substitutions

To enable CSE also inside substitutions (aka B statements) you need to set the preference CSE_SUBST to true. By default, the CSE will only be applied to top-level predicates, such as the invariant, the assertions, the properties or individual predicates inside operations (but not the operation as a whole).

Sharing Predicates

By default ProB's CSE will also share predicates. You can turn off CSE for predicates, i.e., only expressions get shared, by setting the preference CSE_PRED to FALSE. For example, by default ProB's CSE will translate

x+1 > 10 & (x+1 > 10 => y=22)

into

LET @1==(x + 1 > 10) IN @1 & (@1 => y = 22)

After setting CSE_PRED to FALSE, this will be translated into:

LET @0==(x + 1) IN @0 > 10 & (@0 > 10 => y = 22)

Other Preferences

ProB will also share expressions which are potentially not well-defined, and takes extra care with those expressions (in particular in the context of set comprehensions and quantifications). However, you can completely turn off sharing of potentially not-well defined expressions by setting the preference CSE_WD_ONLY to TRUE. For example, by default the following predicate

x>1 & 100/x > 20 & 100/x <26

will get translate into

LET @0==(100 / x) IN (x > 1 & @0 > 20) & @0 < 26)

and ProB will find the solution x=4. With CSE_WD_ONLY to TRUE, the predicate will be left unchanged (and ProB will find the same solution).

Tips

To inspect the effect of CSE, you do one of the following:

• In ProB Tcl/Tk you can use the command "Show Internal Representation" in the Debug menu to inspect the effect of CSE on your machine
• For probcli, you can use the command -pp FILE to write the pretty-printed internal representation of your machine after CSE to a file
• For the REPL of probcli (command -repl), you can use the option -p REPL_UNICODE TRUE to force ProB to print your expressions/predicates after CSE processing (using Unicode characters)

The ProB Search Path

Starting with version 1.5 of ProB, it is possible to customize where the parser will ProB will search for referenced files.

By default ProB will try to find files referenced from a machine (using SEES, INCLUDES, DEFINITON-files, etc) resolving paths as relative to the current machine or within the ProB standard library.

Commonly used files can be placed in a shared location, e.g. in the standard library (the stdlib directory in the ProB distribution) or any custom location.

The search path can be customized by defining a PROBPATH environment variable that contains a list of directories to be searched. On windows the directors are separated by a ";" and on unix systems by a ":" character, e.g.:

On unix:

PROBPATH=~/myproject/common:~/myotherproject/common probcli model.mch

And on windows:

 PROBPATH=~/myproject/common;~/myotherproject/common probcli model.mch

will resolved referenced files relative to model.mch, then in ~/myproject/common then in ~/myotherproject/common and finally in the standard library of ProB, stopping as soon as a file with the name being looked up is found. Warning: Display title "Handbook/Advanced Features" overrides earlier display title "The ProB Search Path".

TLC

As of version 1.4.0, ProB can make use of TLC as an alternative model checker to validate B specifications. TLC is an efficient model checker for TLA+ specifications, which can check LTL properties with fairness. It is particularly good for lower level specifications, where it can be substantially faster than ProB's own model checker. TLC has been released as an open source project, under the MIT License.

How to use TLC

Using TLC in ProB Tcl/Tk

First you have to open a B specification in the ProB GUI. Then you can select the menu command "Model Check with TLC" in the "Verify->External Tools" menu.

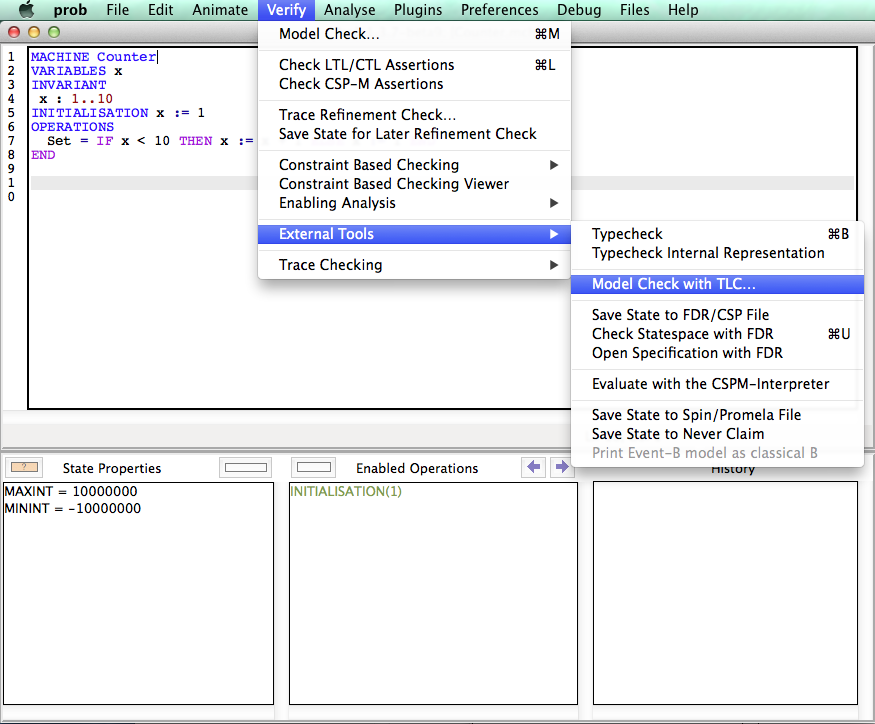
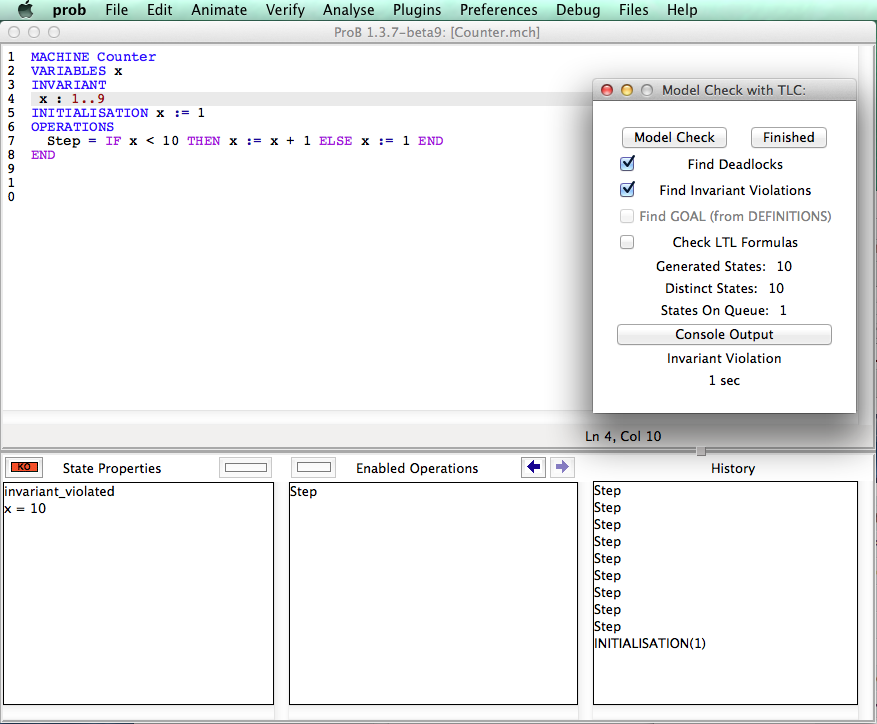
You can use TLC to find the following kinds of errors in the B specification:

• Deadlocks
• Invariant violations
• Assertion errors
• Goal found (a desired state is reached)
• Properties violations (i.e, axioms over the B constants are false)
• Well-definedness violations
• Temporal formulas violations

In some cases, TLC reports a trace leading to the state where the error (e.g. deadlock or invariant violation) occur. Such traces are automatically replayed in the ProB animator (displayed in the history pane) to give an optimal feedback.

Requirements

On Linux the tlc-thread package is required to run TLC from the tcl/tk ui:

sudo apt-get install tcl-thread

Using TLC in probcli

You can use the following switch to use TLC rather than ProB's model checker:

-mc_with_tlc

Some of the standard probcli options also work for TLC:

• -noinv (no invariant checking)
• -nodead (no deadlock checking)
• -noass (no assertion checking)
• -nogoal (no checking for the optional goal predicate)

In addition you can provide

• -noltl (no checking of LTL assertions)

ProB Preferences influencing TLC:

• TLC_WORKERS: influences the number of workers that will be used by TLC; a call might look like this:

probcli FILE.mch -mc_with_tlc -p TLC_WORKERS 2 -noltl

• TLC_USE_PROB_CONSTANTS: setup constants using ProB before applying TLC (can lead to a considerable speed-up); e.g.

probcli FILE.mch -mc_with_tlc -p TLC_USE_PROB_CONSTANTS TRUE

When to use TLC

TLC is extremely valuable when it comes to explicit state model checking for large state spaces. Otherwise, TLC has no constraint solving abilities.

Translation from B to TLA+

TLC is a very efficient model checker for specifications written in TLA+. To validate B specification with TLC we developed the translator TLC4B which automatically translates a B specification to TLA+, invokes the model checker TLC, and translates the results back to B. Counter examples produced by TLC are double checked by ProB and replayed in the ProB animator. The translation to TLA+ and back to B is completely hidden to the user. Hence, the user needs no knowledge of TLA+ to use TLC.

The following article describes the translation in more detail:

• Dominik Hansen and Michael Leuschel. Translating B to TLA+ for validation with TLC. Sci. Comput. Program. 131, pages 109-125. 2016. Link.

Limitations

The following constructs are currently not supported by the TLC4B translator:

• Refinement specifications
• Machine inclusion (SEES, INCLUDES, ..)
• Sequential composition (G;H) with variables assigned more than once

Visited States

Sometimes TLC will show a different number of visited states compared to the ProB model checker. The following example should illustrate this issue:

MACHINE NumberOfStates
CONSTANTS k
PROPERTIES
 k : 1..10
VARIABLES x
INVARIANT
 x : NATURAL
INITIALISATION x := k
END

ProB will report 21 distinct states (1 root state, 10 constant setup states, 10 initialization states):

TLC will only report 10 distinct states (10 initialization states).

More Information

More information can be found in our article which is an extended version of the ABZ'2014 conference paper:

• Dominik Hansen and Michael Leuschel. Translating B to TLA+ for validation with TLC. Sci. Comput. Program. 131, pages 109-125. 2016. Link.

Generating Documents with ProB and Latex

ProB can (as of version 1.6.1) be used to process Latex files, i.e., the command-line tool probcli scans a given Latex file and replaces certain commands by processed results.

Usage

A typical usage would be as follows:

   probcli FILE -init -latex Raw.tex Final.tex

Note: the FILE and -init commands are optional; they are required in case you want to process the commands in the context of a certain model. Currently the probcli Latex commands mainly support B and Event-B models, TLA+ and Z models can also be processed but all commands below expect B syntax. You can add more commands if you wish, e.g., set preferences using -p PREF VAL or run model checking --model-check. The Latex processing will take place after most other commands, such as model checking.

You will probably want to put the probcli call into a Makefile, in particular when you want to generate dot graphics using ProB.

The distribution folder of ProB contains an example with a Makefile, producing the following file, which at the same time documents the core features:

File:Prob latex doc.pdf

Commands

The commands are described in the PDF document above. Here is a short summary of some of the commands:

• \probexpr{EXRP} command takes a B expression EXPRas argument and evaluates it. By default it shows the B expression and the value of the expression. Example: \probexpr{{1}\/{2**10}} will be replaced by {1,1024}
  • ascii to print the result as ASCII rather than using Latex math symbols
  • time to display the time taken for the command
  • string the result value is a string, and do not print the quotes around the string
  • value to just print the value, not the expression

• \probrepl{CMD} command takes a probcli REPL command CMD as argument and executes it. By default it shows only the output of the execution, e.g., in case it is a predicate TRUE or FALSE. Example: \probrepl{let DOM = 1..3}. A variation of the latter is the new command \problet{DOM}{1..3} which shows the let construct itself within the generated Latex. Optional arguments for \probrepl are :
  • solution to display the solution bindings (for existential variables) found by ProB
  • store to store the solution bindings as local variables (similar to let)
  • ascii to print the result as ASCII rather than using Latex math symbols
  • time to display the time taken for the command
  • print to print the expression/predicate being evaluated (automatically set by \problet
  • silent to not print the result of the evaluation

• \probtable{EXRP} command takes a B expression EXPRas argument, evaluates it and shows it as a Latex table. Optional arguments are no-tabular, no-hline, no-headings, no-row-numbers, max-table-size=NR.

• \probdot{DOT}{File1} command takes a B expression EXPRas argument, evaluates it as a graph and writes a dot file File1. You can provide a second File as argument, in which case dot is called to generate a PDF document. You can also set sfdp as third argument, in which case the sfdp tool will be used instead of dot.

• \probprint{EXRP} command takes a B expression or predicate EXPRas argument and pretty prints it. Optional arguments are:
  • pred only try to parse first argument as predicate
  • expr only try to parse first argument as expression
  • ascii to print the result as ASCII rather than using Latex math symbols

• \probif{EXPR}{Then}{Else} command takes an expression or predicate EXPR and two Latex texts. If the expression evaluates to TRUE the first branch Then is processed, otherwise the other one Else is processed.

• \probfor{ID}{Set}{Body} command takes an identifier ID, a set expression Set and a Latex text Body, and processes the Latex text for every element of the set expression, setting the identifier to a value of the set.

Some Examples

• Presentation held in Grenoble in September 2016 about "Constraint Programming Puzzles in B" File:Puzzle latex presentation.pdf
• SBMF'2016 keynote article "Formal Model-Based Constraint Solving and Document Generation" File:Sbmf 2016 latex.pdf

Using ProB with Atelier B

Atelier B Plugin

ProB Tcl/Tk can be installed as a plugin for Atelier B, so that ProB can be launched directly from within Atelier B projects. With this you can animate and model check B machines directly from within the IDE of Atelier-B.

The easiest is to perform the menu command "Install AtelierB 4 Plugin..." in the Help menu of ProB Tcl/Tk. This will create a file called probtclk.etool in an extensions folder next to Atelier B's bbin folder. The extensions folder is created if necessary.

Note: as the layout of Atelier-B's directories has changed, you need to use ProB 1.12.0 or newer for Atelier-B 4.7.1 or newer on macOS. You can also create the the above file yourself.

Here is a typical probtclk.etool file (where PathToProB depends on your location of the ProB installation folder containing the prob and probcli binaries):

<externalTool category="component"   name="ProBTclTk" label="&Animate with ProB (Tcl/Tk)">
    <toolParameter name="editor" type="tool" configure="yes"
   default="PathToProB/StartProB.sh" />
    <command>${editor}</command>
    <param>${componentPath}</param>
 </externalTool>

Note, you can also ProB2-UI within Atelier-B by creating a suitable file prob2ui.etool in this extensions folder. Here is a typical file for macOS; the path needs to be adapted for your location and operating system (we plan to provide an installer within ProB2-UI):

<externalTool category="component"   name="ProB2UI" label="&Animate with ProB2-UI">
    <toolParameter name="editor" type="tool" configure="yes"
   default="/Applications/Development/ProB/ProB 2 UI.app/Contents/MacOS/ProB 2 UI" />
    <command>${editor}</command>
    <param>--machine-file</param>
    <param>${componentPath}</param>
</externalTool>

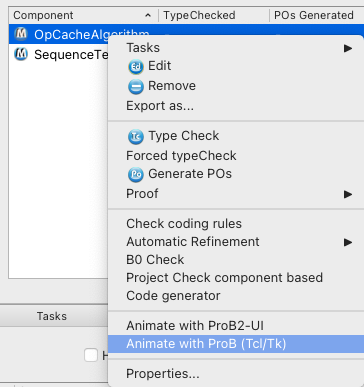
After installing the plugins you can launch ProB for selected B machines by right-clicking on a B machine within Atelier B:

ProB as Atelier B Prover

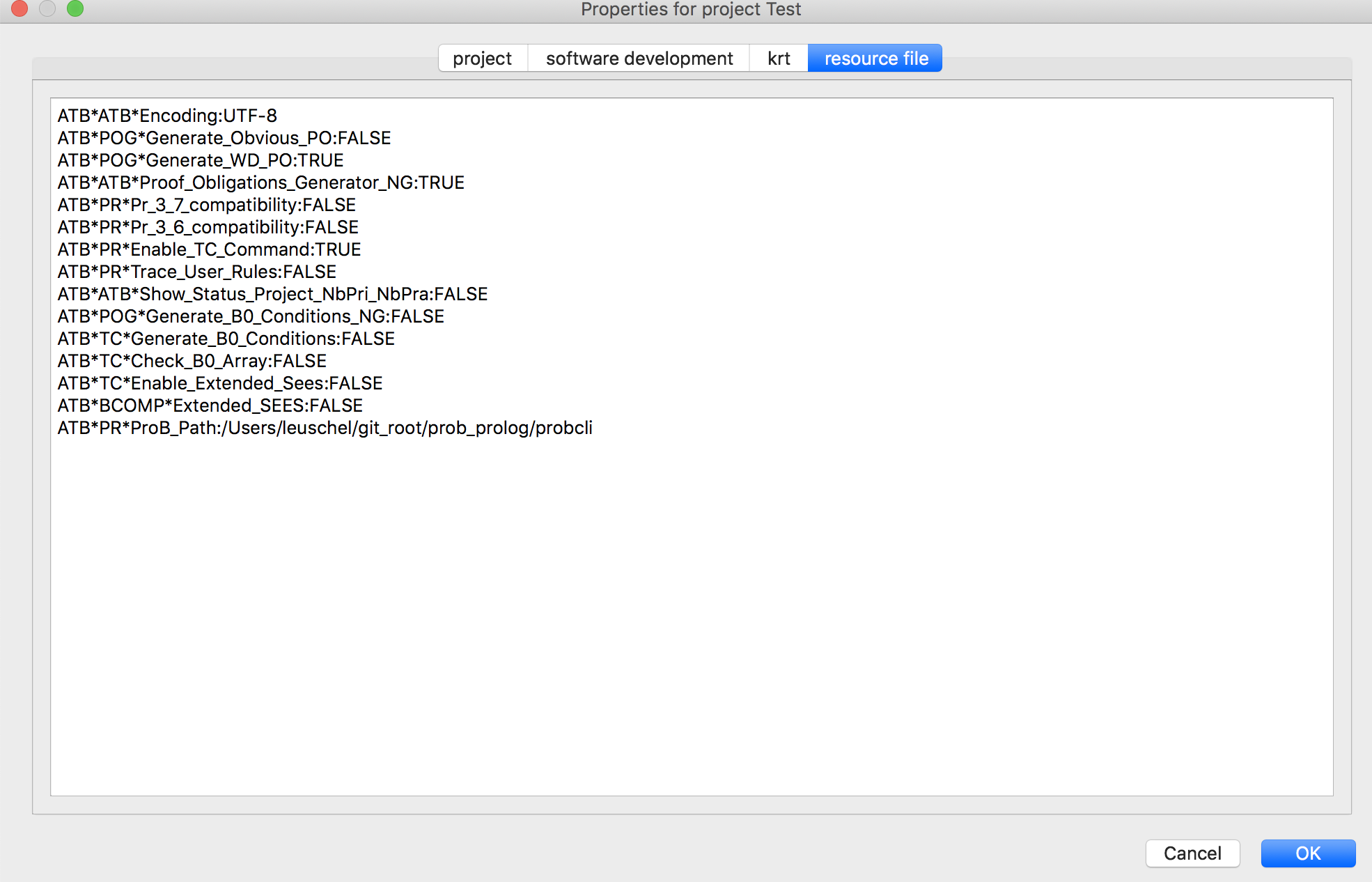
Atelier B also enables to use ProB as a prover/disprover in the interactive proof window. For this you need to set the ProB_Path resource to point to probcli (command-line version of ProB). To do this you need to add the following line to the resource file of your project (replacing PATH by the the path on your machine to probcli):

ATB*PR*ProB_Path:PATH/probcli

Then you can type, e.g., the command prob(1)in the interactive proof window.

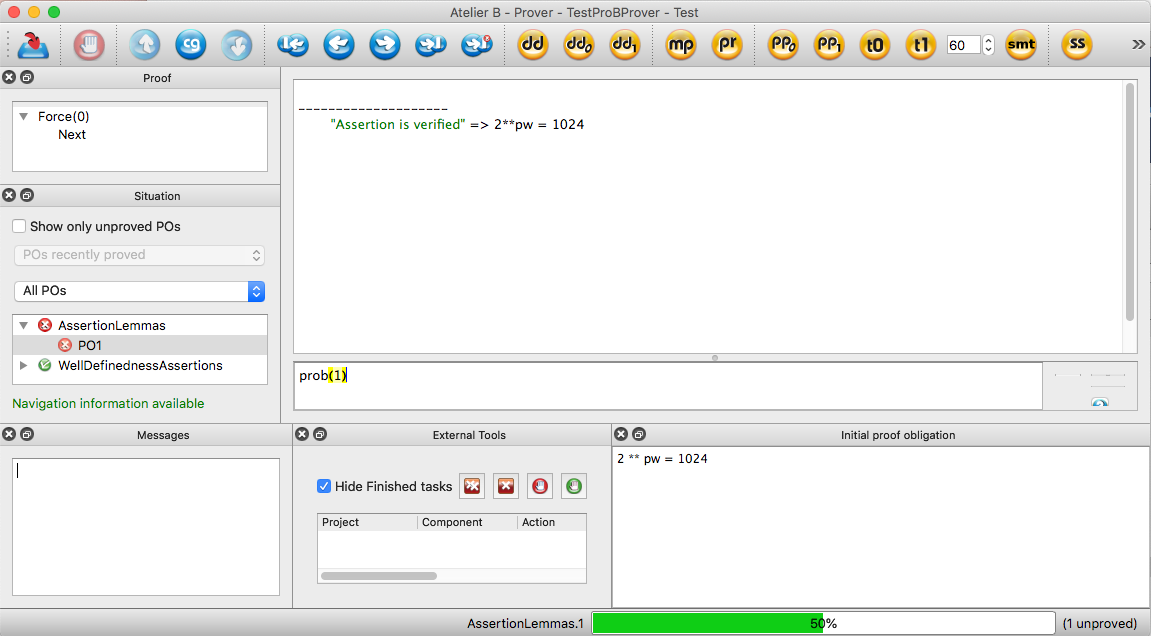
Two commands are provided within Atelier-B:

• prob(n) tries to prove the goal with the selected hypotheses (selected using rp.n as is done for th e pp command of Atelier-B)
• prob(n|t) is similar but also limits the execution time of ProB to t seconds

Atelier-B will call probcli using the commands -cbc_assertions_tautology_proof and -cbc_result_file after having encoded the proof obligation into the ASSERTIONS clause of a generated B machine.

The generated machine typically has the form:

MACHINE probNr
SETS ...
CONSTANTS ...
PROPERTIES
  << ALL HYPOTHESES >>
ASSERTIONS
  ( <<SELECTED HYPOTHESES >>
   =>
  << PROOF GOAL >>
  )
END

Differences with Atelier B

As of version 1.3, ProB contains a much improved parser which tries be compliant with Atelier B but provides extra features.

Extra Features of ProB

• Identifiers: ProB also allows identifiers consisting of a single letter. ProB also accepts enumerated set elements to be used as identifiers. Arbitrary identifiers can be used in backquotes (e..g, `id-1*`)

• Lexing: The Atelier-B parser (bcomp) reports a lexical error (illegal token |-) if the vertical bar (|) of a lambda abstraction is followed directly by the minus sign.

• Typing:
  • ProB makes use of a unification-based type inference algorithm. As such, typing information can not only flow from left-to-right inside a formula, but also from right-to-left. For example, it is sufficient to type xx<:yy & yy<:NAT instead of typing both xx and yy in ProB.
  • Similar to Rodin, ProB extracts typing information from all predicates. As such, it is sufficient to write xx/:{1,2} to assign a type to xx.
  • the fields of records are normalized (sorted); hence the predicate rec(a:0,b:1) = rec(b:y,a:x) is correctly typed for ProB.
  • As of version 1.12.1 you can apply prj1 and prj2 without providing the type arguments. For example, you can write prj2(prj1(1|->2|->3)) instead of prj2(INTEGER,INTEGER)(prj1(INTEGER*INTEGER,INTEGER)(1|->2|->3)).

• DEFINITIONS: the definitions and its arguments are checked by ProB. We believe this to be an important feature for a formal method language. However, as such, every DEFINITION must be either a predicate, an expression or a substitution. You cannot use, for example, lists of identifiers as a definition. Also, for the moment, the arguments to DEFINITIONS have to be expressions. Finally, when replacing DEFINITIONS the associativity is not changed. E.g., with PLUS(x,y) == x+y, the expression PLUS(2,3)*10 will evaluate to 50 (and not to 32 as with Atelier-B).

• for a LET substitution, Atelier-B does not allow introduced identifiers to be used in the right-hand side of equations; ProB allows LET x,y BE x=2 & y=x*x IN ... END but only if the preference ALLOW_COMPLEX_LETS is set to TRUE.

• ProB allows WHILE loops and sequential composition in abstract machines

• ProB now allows the IF-THEN-ELSE for expressions and predicates: IF x<0 THEN -x ELSE x END

• ProB now allows LET constructs for expressions and predicates

• ProB allows btrue and bfalse as predicates.

• ProB allows to use the Event-B relation operators <<->, <->>, <<->>

• ProB allows escape codes (\n, \', \", see above) and supports UTF-8 characters in strings, and ProB allows multi-line string literals written using three apostrophes ("'string'") as well as template strings using three backquotes (e.g., ```1+2=${1+2}```)

• ProB allows WHILE loops and sequential composition in abstract machines

• Some of the sequence operators can be applied to strings (unless you set the preference STRING_AS_SEQUENCE to FALSE): size, rev, ^, conc

• As of version 1.12.1 you can write Event-B style set comprehensions with an extra expression like {x•x:1..10|x*x}. You have to use the middle dot, the bullet (•) or a Unicode dot for this, though.

• ProB comes with several libraries of external functions for string manipulations, mathematical functions, Hilbert's choice operator, etc.

Differences

• for ProB the order of fields in a record is not relevant (internally the fields are sorted), Atelier-B reports a type error if the order of the name of the fields changes

• Well-definedness: ProB will try to check if your predicates are well-defined during animation or model checking, but there is currently no guarantee that all well-definedness errors will be detected. To be on the safe side, you should ensure that your formulas are well-defined according to the left-to-right definition of well-definedness employed in Rodin for Event-B. ProB now has a static checker for well-definedness which you can use for this. Note, however, that ProB may re-order conjuncts if this improves well-definedness. For example, for x:0..3 & y=10/x & x /=0 ProB will not report an error as the conjunct x/=0 is processed before the division. Indeed, while this predicate is not well-defined according to Rodin's left-to-right rule, it is well-defined according to the more liberal commutative definition of well-definedness.

Limitations

• Parsing: ProB will require parentheses around the comma, the relational composition, and parallel product operators. For example, you cannot write r2=rel;rel. You need to write r2=(rel;rel). This allows ProB to distinguish the relational composition from the sequential composition (or other uses of the semicolon). You also generally need to put BEGIN and END around the sequential composition operator, e.g., Op = BEGIN x:=1;y:=2 END.
• Similarly, tuples without parentheses are not supported; write (a,b,c) instead of a,b,c

• Unsupported Operators:
  • Trees and binary trees: most but not all tree operators (mirror, infix) are supported yet. These operators may disappear in future version of Atelier B and may also disappear from ProB.
  • VALUES: This clause of the IMPLEMENTATION machines is not yet fully supported;

• There are also some general limitations wrt refinements. See Current Limitations#Multiple Machines and Refinements for more details.

Using ProB with KODKOD

As of version 1.3.5 ProB can make use of Kodkod as an alternate way of solving constraints. Kodkod provides a relational interface to SAT solvers and is the heart of the Alloy tool.

How to enable Kodkod

For the command-line version you need to call prob as follows:

probcli -p KODKOD TRUE

Note: to experiment with Kodkod you may want to try out the command:

probcli -p KODKOD TRUE -repl

If in addition you want see a graphical representation of the solutions found you can use the following command and open the out.dot file using dotty or GraphViz:

probcli -p KODKOD TRUE -repl -evaldot ~/out.dot

For the ProB Tcl/Tk Version you should select the menu command "Enable Kodkod for Properties" in the Preferences menu.

What can be translated

• Types:
  • Basic Types: Deferred Sets, enumerated sets, integers, booleans
  • Sets of basic types
  • Relations between basic types
  • Higher-order types (sets of sets) are not supported

• Operators:
  • Predicates: &, or, =>, <=>, not, !, #, =, /=
  • Booleans: TRUE, FALSE, BOOL, bool(...)
  • Sets: {..,...} {x|P}, POW, card, Cartesian product, \/, /\, -, :, /:, /<:, <<: /<<:
  • Numbers: n..m, >, <, >=, <=, +, -, *, SIGMA(x).(P|x)
  • Relations: <->, |->, dom, ran, id, <|, <<|, |>, |>>, ~, [...], <+, prj1, prj2, closure1
  • x : S+->T, x:S-->T, ..., lambda
  • currently no operations on sequences are supported

• Some limitations:
  • If integers are used, a predicate can only be translated if a static analysis can estimate the interval of its possible values.
  • Generally only complete predicates are translated or nothing at all, unless you set the KODKOD_ONLY_FULL preference to FALSE.

When is the Kokod translation used

Once enabled, the Kodkod translation will be used in the following circumstances:

• for solving PROPERTIES
• constraint-based assertion checking (-cbc_assertions command for probcli or the "Check Assertions on Constants" command in the menu Verify -> Constraint-Based Checking)
• constraint-based deadlock checking
• in the Eval Console in the ProB Tcl/Tk version
• for the REPL in probcli (probcli -p KODKOD TRUE -repl)

SAT solver

By default Kodkod in ProB uses the bundled SAT4J solver. You can switch to using minisat by putting a current version of libminisat.jnilib into ProB's lib directory.

Similarly, as of ProB 1.6.1-beta5 you can also use the Solver lingeling or glucose by dropping liblingeling.dylib or libglucose.dylib into ProB's lib folder (for Mac OS X; for Linux the extension will be different). You can control the solver being used using the KODKOD_SAT_SOLVER preference (which has four possible values: sat4j, minisat, lingeling, glucose).

These files can be downloaded from the Kodkod download site.

More Preferences

If you set KODKOD_ONLY_FULL to FALSE, then the Kodkod translation can be applied to part of a predicate. In other words, the predicate (such as the PROPERTIES) are partitioned into two parts: one that can be understood by Kodkod and the rest which will be dealt with by ProB's solver.

You can also enable symmetry by using the preference KODKOD_SYMMETRY. By default, ProB will set this value to 0, i.e., symmetry is off. This means that Kodkod can also be used within set comprehensions. By setting the preference to a value higher than 0 you will enable symmetry within Kodkod, which may mean that not all solutions will be returned. Setting the value too high may be counter productive; Kodkod's recommended default is 20.

Finally, you can control the number of solutions that Kodkod computes in one go using the preference KODKOD_MAX_NR_SOLS. E.g., if you are interested in only one solution and KODKOD_ONLY_FULL is TRUE, then you should set this value to 1.

More details

• Plagge, Leuschel. Validating B, Z and TLA+ using ProB and Kodkod. In Proceedings FM'2012, Dimitra Giannakopoulou and Dominique Méry, LNCS 7436, Springer, 372--386, 2012. (pdf)

You can also have a look at these Wiki pages:

• Proving_Theorems_in_the_ProB_REPL
• Argumentation Theory Example

Using ProB with Z3

The current nightly versions of ProB can make use of Z3 as an alternate way of solving constraints.

How to use Z3 within ProB

One can start a REPL (Read-Eval-Print-Loop) by starting probcli with the '-repl' command line option. Any predicate preceded with :z3 will be solved by Z3 considering the current machine's state. The command :z3-free can be used to solve a constraint without considering the current machine's state. The full integration of Z3 and ProB’s kernel can be enabled by setting the corresponding preference by passing

-p SMT SUPPORTED INTERPRETER TRUE

on the command line.

How to install Z3 for ProB

For Linux and Mac OS, the extension is built on our infrastructure and ships with the regular ProB download. You don't need to install Z3 on your system.

What can be translated

Currently, the Z3 translation is unable to cope with the following constructs:

• Generalised concatenation
• Permutation
• Iteration and Closure

When using Z3 alone, the solver will report "unsupported_type_or_expression" if it can not handle parts of a constraint.

When used together with ProB, everything Z3 can not be coped with will be handled by ProB alone automatically.

Examples

Using the repl, one can try out different examples.

First an example which can be solved by Z3 and not by ProB:

>>> X<Y & Y<X & X:INTEGER
% Timeout when posting constraint:
% kernel_objects:(_981727#>0)
### Warning: enumerating X : INTEGER : inf:sup ---> -1:3
Existentially Quantified Predicate over X,Y is UNKNOWN
[FALSE with ** ENUMERATION WARNING **]

Using the Z3 translation it can be solved:

>>> :z3 X<Y & Y<X & X:INTEGER
PREDICATE is FALSE

Here an example that shows that Z3 can be used to solve constraints and obtain solutions for the open variables:

>>> :z3 {x} /\ {y} /= {} & x:1000000..20000000 & y>=0 & y<2000000
PREDICATE is TRUE
Solution:
      x = 1000000
      y = 1000000

As of version 1.10.0-beta4 you can also issue the <t>:z3-version</t> command in the REPL to obtain version information.

More details

A paper describing the integration of ProB and Z3 has been published at iFM 2016. You can download the

• raw data from our benchmarks including the R scripts to generate the
• resulting graphs.

A journal paper describing an extended interface to Z3 and alternative translation from B to SMT-LIB using Lambda functions has been published in the International Journal on Software Tools for Technology Transfer in 2022.