Also see the following tutorials:

Other languages

Since version 1.2.7 of ProB (July 2008) you can also open Promela files with ProB. This mode is still experimental but already very usable and provides source-level highlighting during animation. The main purpose is to debug and animate Promela specifications in a user-friendly way. We do not plan to compete in terms of model checking speed with Spin (Spin compiles Promela to C code, ProB uses a Prolog interpreter). To animate a Promela model, simply open the file with the .pml or .prom extension with the "File->Open..." command. You will have to choose "Other Formalisms" or "All Files" in the filter pop-up-menu to be able to select the file.

You can also use ProB to animate and model check other specification languages by writing your own Prolog interpreter. To do this you should create a Prolog file with the .P extension and which defines three predicates:

trans/3: this predicate should compute for every state (second argument), the outgoing transitions (first argument), and the resulting new states (third argument)
prop/2: this predicate should compute the properties for the states of your system
start/1: this defines the initial states of your system

For example, the following defines a system with two states (a and b) and two transitions (lock and unlock):

start(a). trans(lock,a,b). trans(unlock,b,a). prop(X,X).

These Prolog files can be loaded with ProB's open command (be sure to use the .P extension and to either choose "All files" or "Other Formalisms" in the file filtering menu).

Another simple example for a very basic process algebra is as follows:

% start(PossibleInitialState)
start(choice(pref(a,stop),intl(pref(b,pref(c,stop)),pref(d,stop)))).

% trans(Event, StateBefore, StateAfter)
trans(A,pref(A,P),P). % action prefix
trans(A,intl(P,Q),intl(P2,Q)) :- trans(A,P,P2). % interleave
trans(A,intl(P,Q),intl(P,Q2)) :- trans(A,Q,Q2).
trans(A,par(P,Q),par(P2,Q2)) :- trans(A,P,P2), trans(A,Q,Q2). % parallel composition
trans(A,choice(P,Q),P2) :- trans(A,P,P2). % choice
trans(A,choice(P,Q),Q2) :- trans(A,Q,Q2).

% prop(State, PropertyOfState)
prop(pref(A,P),prefix).
prop(intl(P,Q),interleave).
prop(A,A).

If you have a working interpreter, you can also contact the ProB developers in order for your interpreter to be included in the standard ProB distribution (in the style of the CSP-M or Promela interpreters). With this you can add syntax highlighting, error highlighting in the source code, highlighting during animation, support for new LTL properties,...

Another, slightly more elaborate example, is the following interpreter for regular expressions:

/* A simple animator for regular expressions */

start('|'('.'('*'(a),b) ,  '.'('*'(b),a))). 

trans(_,[],_) :- !,fail.
trans(X,X,[]) :- atomic(X),!.
trans(X,'|'(R1,R2),R) :- 
 trans(X,R1,R) ; trans(X,R2,R).
trans(X,'.'(R1,B),R) :- trans(X,R1,R2),
 gen_concat(R2,B,R).
trans(X,'?'(R1),R) :-
 trans(X,R1,R) ; (X=epsilon,R=[]).
trans(epsilon,'*'(_R1),[]). 
trans(X,'*'(R1),R) :- 
 trans(X,R1,R2),
 gen_concat(R2,'*'(R1),R).
trans(X,'+'(R1),R) :- 
 trans(X,R1,R2),
 gen_concat(R2,'*'(R1),R).

gen_concat(R1,R2,R) :- 
 (R1=[] -> R = R2 ; R = '.'(R1,R2)).

prop(X,X).

Finally, a more complex example is an encoding of the Rush Hour puzzle which also includes a graphical visualisation (using the animation_function_result predicate recognised by ProB as of version 1.4.0-rc3).

Other recognised Prolog predicates

The following can be used to set up an animation image matrix with corresponding actions:

animation_image(Nr,Path)
animation_function_result(State,List) where List is a list of terms of the form ((Row,Col),Img) where Img is either a declared animation_image number or another Prolog term
animation_image_right_click_transition(Row,Col,TransitionTemplate)
animation_image_click_transition(FromRow,FromCol,ToRow,ToCol,ListOfTransitionTemplates,ImageNr)

ProB for Event-B

In addition to classical B (aka B for software development), ProB also supports Event-B and the Rodin platform. ProB can be installed as a plugin for Rodin. Once installed, one can export contexts and models as *.eventb files and use them within ProB Tcl/Tk and the command-line version probcli.

See the tutorial pages for more information about using ProB for Event-B:

The Rodin handbook also contains material about ProB:

ProB for Rodin

Currently there are two versions of ProB available for Rodin.

ProB (1) for Rodin

The first one is based on the old Java API and supports Rodin 2.8 and Rodin 3.3. The update site comes built in into Rodin, see the tutorial on installing ProB for Rodin. Nightly releases of this versions are also available on the Download page.

ProB 2.0 for Rodin

The second, still experimental, one is based on the new ProB Java API (aka ProB 2.0). Because the UI components provided by the ProB Java API are based on web technologies, we were able create a simple plugin for the Rodin 3 tool that provides the user with all of the functionality of ProB within Rodin. The plugin uses views with embedded Eclipse SWT browsers to access the user interface components that are shipped with the ProB Java API library. Details about nightly releases of this versions is also available on the Download page.

Multi-Simulation for Rodin based on ProB

There is now also a Multi-Simulation Plug-in available for Rodin. It enables discrete/continuous co-simulation.

Other Plug-Ins for Rodin

Prover Evaluation

This Plug-in is available at the update site http://nightly.cobra.cs.uni-duesseldorf.de/rodin_provereval/ and is capable to evaluate a variety of provers or tactics on a selection of proof obligations.

Camille

We also develop the Camille text-editor for Rodin. The update site (https://www3.hhu.de/stups/rodin/camille/nightly/) is preconfigured within Rodin. More information can be found on the Camille site at event-b.org.

Event-B

ProB supports animation and model-checking for Event-B specifications.

Installation

To install the ProB plugin for Rodin, open the "Help" menu in Rodin and click "Install new software".

You see a drop-down list titled "Work with:" at the top of the install dialog. Choose the update site "ProB - ..." and click on "ProB for rodin2" in the field below. Click on the "Next" button at the button on the dialog and proceed with the installation as usual.

Alternativaly, one can use the Tcl/Tk version of ProB but Event-B models must be exported to an .eventb file first (see below).

Animation and Modelchecking

You can start animation of a model (machine or context) by right-clicking on the model in the Event-B explorer. Choose "Start Animation / Model Checking".

TODO: Here we should add more details about the ProB perspective and views.

Export for use with the Tcl/Tk version of ProB

You can export a model (machine or context) to an .eventb - file by right-clicking on the model in the Event-B explorer. You can find the corresponding menu item right below the animation item.

Such a .eventb file can be opened by the command line and Tcl/Tk version of ProB.

Theories

ProB has (limited) support for theories.

Currently supported are (examples refer to the theory project below):

recursive datatypes (e.g. the List datatype)
operators defined by direct definitions (e.g. operators in the BoolOps theory) or recursive definitions (e.g. operators in the List theory)
special annotated operators (see below)

Axiomatically defined operators are not supported without additional annotations.

Tagging operators

ProB has some extra support for certain operators. ProB expects an annotation to an operator that provides the information that it should use a specific implementation for an operator. Such tags are given in a .ptm file (ProB Theory Mapping). The file must have the same name as the theory.

For each annotated operator, the file contains a line of the form

operator Name internal {Tag}

where Name is the name of the operator in the theory and Tag is a ProB internal name.

The use of these tags is usually for experts only. In the theory file below, some of the theories are annotated.

Currently are the following tags supported:

Tag	Description	Expected type
closure1	the transitive closure	POW(T**T)
SIGMA	the sum of a set	POW(T**INT)
PI	the product of a set	POW(T**INT)
mu
choose
mkinat(op1,op2)

TODO: to be continued...

Download Theories

An example project with theories: media:theories2.zip

TODO: A description of the supported parts.

Event-B Theories

ProB has (limited) support for theories.

Currently supported are (examples refer to the theory project below):

recursive datatypes (e.g. the List datatype)
operators defined by direct definitions (e.g. operators in the BoolOps theory) or recursive definitions (e.g. operators in the List theory)
special annotated operators like transitive closure (see below)

Axiomatically defined operators are not supported without additional annotations.

Download Theories

An example project with theories: media:theories2.zip

The project contains the following theories:

SUMandPRODUCT: Contains two operators SUM and PRODUCT which take a set of the type POW(T**INT) as argument (with T being a type variable) and return the sum (resp.) product of all element's integer value.

The operators are annotated such that ProB uses an extra implementation.

Seq: The theory of sequences provides operators for sequences that are defined by direct definitions, thus supported by ProB.
Real (unsupported): A theory of real numbers, currently unsupported by ProB.
Natural: A theory of inductive naturals (defined by a constant zero and a successor function).; The mkinat operator is annotated such that ProB uses an explicit implementation.
List: A theory of lists that are either empty or have a head and a tail
FixPoint (not really supported): The theory is defined by direct definitions but they usually get so complex that ProB cannot cope with them.
closure: The operator for transitive closure is supported by ProB.; The operator is annotated such that ProB uses the classical B implementation.
Card (contains no operators or data types): Contains theorem about set cardinalities.
BoolOps: Operators on Booleans (e.g. AND, OR) are defined by direct definitions and as such supported by ProB.
BinaryTree: Binary Trees are supported by ProB.

Tagging operators

Please note: The use of these tags is for experts only. Normally such annotations are delivered with a theory. If you think ProB should provide specific support for a theory, please contact us.

ProB has some extra support for certain operators. ProB expects an annotation to an operator that provides the information that it should use a specific implementation for an operator. Such tags are given in a .ptm file (ProB Theory Mapping). The file must have the same name as the theory.

For each annotated operator, the file contains a line of the form

operator Name internal {Tag}

where Name is the name of the operator in the theory and Tag is a ProB internal name.

Currently are the following tags supported (with T being an arbitrary type):

Tag	Description	Expected type	Return type
closure1	the transitive closure	POW(T**T)	POW(T**T)
SIGMA	the sum of a set	POW(T**INT)	INT
PI	the product of a set	POW(T**INT)	INT
mu	returns the element of a singleton set	POW(T)	T
choose	returns (deterministically) one element of a non-emtpy set	POW(T)	T
mkinat(zero,succ)	returns an inductive natural number where zero and succ are the two operators of a natural number datatype with zero having no args and succ having one arg (an inductive natural)	INT	Inductive Nat

As of version 1.12 (mid-september 2022) ProB also transparently accepts POW(INT) as type for SIGMA and PI. It now also accepts many of its external functions as tag names, such as the the functions from LibraryStrings.def or LibraryReals.def. For example, here we map the operator plus to ProB's external function RADD for adding two reals:

operator "plus" internal {RADD}

If you set the preference AUTO_DETECT_THEORY_MAPPING to TRUE then ProB will work with several standard Rodin theories even without a .ptm file in the workspace.

As of version 1.13 (November 2023) ProB also accepts literals as well as formulas between dollars in the .ptm files. For example, here the operator Rone is defined by the literal 1.0 and the operator RRealPlus by an expression (a set comprehension of the positive reals annotated with the symbolic pragma):

operator "Rone" internal {1.0}
operator "RRealPlus" internal {$/*@symbolic*/ {x|x:REAL & x>= 0.0}$}

Error Messages

In case the .ptm file is missing, you will get an error message such as the following one:

Axiomatic defined operator "SUM" not recognized.

Examples

For reference, here are the contents of some of the .ptm files. In case of an error message, you can copy these files into your Theory Projects (e.g., using Drag & Drop) and then refresh (F5). After that animation with ProB should work.

SUMandPRODUCT.ptm

operator "SUM" internal {SIGMA}
operator "PRODUCT" internal {PI}

closure.ptm

operator "cls" internal {closure1}

Natural.ptm

operator "mk_iNAT" internal {mkinat}

Here are the contents for a Reals theory by Guillaume Dupont:

operator "RReal" internal {REAL}
operator "Rone" internal {1.0}
operator "Rzero" internal {zero}
operator "Rtwo" internal {two}
operator "plus" internal {RADD}
operator "times" internal {RMUL}
operator "minus" internal {RSUB}
operator "lt" internal {RLT}
operator "leq" internal {RLEQ}
operator "gt" internal {RGT}
operator "geq" internal {RGEQ}
operator "uminus" internal {RSUB}
operator "inverse" internal {RINV}
operator "divide" internal {RDIV}
operator "abs" internal {RABS}
operator "sqrt" internal {RSQRT}
operator "Rmax" internal {RMAXIMUM}
operator "Rmin" internal {RMINIMUM}
operator "RRealPlus" internal {$/*@symbolic*/ {x|x:REAL & x>= 0.0}$}
operator "RRealMinus" internal {$/*@symbolic*/ {x|x:REAL & x<= 0.0}$}
operator "RRealStar" internal {$/*@symbolic*/ {x|x:REAL & x /= 0.0}$}
operator "RRealPlusStar" internal {$/*@symbolic*/ {x|x:REAL & x> 0.0}$}
operator "RRealMinusStar" internal {$/*@symbolic*/ {x|x:REAL & x< 0.0}$}

CSP-M

ProB supports machine readable CSP^[1] as supported by FDR and ProBE. CSP files can be animated and model checked on their own simply by opening a file ending with ".csp".

You can also use a CSP file to guide a B machine by first opening the B machine and then using the "Open Special" sub-menu of the File menu:

use CSP file: uses the CSP file to control the current B machine (see below)
use default CSP file: trys to use a CSP with the same name as the current B machine to control it

Limitations of CSP-M Support

ProB now supports FDR and ProBE compatible CSP-M syntax, with the following outstanding issues

currying and lambda expressions have only been partially tested
extensions and productions are not yet supported (but {| |} is)
the priority of rename compared to external choice is unfortunately different than in FDR; please use parentheses
mixing of closure with other set operations (especially diff) is not yet fully supported
input patterns can only contain variables, tuples, integers and constants (ch?(x,1) is ok, ch?(y+1,x) not). Also, for a record, all arguments must be provided (e.g., for datatype r.Val.Val you have to write r?x?y you cannot write r?xy). Finally, for the moment within "ch? x.y:Set" the ":Set" associates only with y; if you want to check that "x.y" is in Set you need to write: "ch?(x.y):Set.
channel declarations can either use associative dot tuples or non-associative tuples but not yet both. Also, sets of tuples as channel types will not work the same way as in FDR. I.e., for channel a:LinkData you should not use LinkData = {0.0, 0.1, 1.0, 1.1} but rather nametype LinkData = {0,1}.{0,1}.

Also, in the first phase we have striven for compatibility and coverage. We still need to tune the animator and model checker for efficiency (there are few known bottlenecks which will be improved, especially with deeply nested CSP synchronization constructs).

Guiding B Machines with CSP

To use this feature of ProB: first open a B Machine, then select "Use CSP File to Guide B..." or "Use Default CSP File" in the "Open Special" submenu of the File menu (you must be in normal user mode to see it).

The CSP file should define a process called "MAIN". This process will be executed in parallel with the B machine. The synchronization between the B machine and the CSP specification is as follows:

CSP events that have the same name as B Operations will synchronize with B; CSP events that have the same name as a B Variable or Constant can be used to inspect the current value of these, all other CSP events can happen independently of B. In CSP terms the CSP and B are composed as follows:
```
 CSP [| {op1,...,opn} |] B
```
where op1,...,opn are the visible operations defined in the B machine.
CSP events do not need to provide all arguments of B operations:

add!1 -> will match add(1,1) or add(1,2) or ... 
(supposing add has 2 parameters in B)
add -> will match add(1,2), add(2,1), ...

add!1!2 -> will only match add(1,2)

B Output arguments are specified at the end
```
lookup!X!2 will match lookup(X) --> 2
```
Note however, that for non-deterministic operations you generally should only retrieve the output value using a ? and not match against it using a !. Otherwise, the non-determinism of the B operation will be treated as an external choice for the CSP. So, if lookup is non-deterministic then we should do lookup!X?Res -> Res=2 & Cont rather than lookup!X!2 -> Cont.
If you have a variable called vv, then you can use vv?VAL to get the value of vv. You can also use, for example, vv!X to check that the value is equal to X. If vv is a relation or function, then you can also use two values on the channel to check for particular tuples in the relation. For example, use vv!3?Y to check whether tuples (3,Y) are in the relation vv (there will be one possible synchronisation per such value).
see the file "bookstore_guide.csp" in the provided Machines directory for an example.

For the syntax definition see CSP-M Syntax

Command Line option for guided CSP||B

From the command line, you can specify a CSP File that should be used to guide the B machine with

-csp-guide <Filename>

(This feature is included since version 1.3.5-beta7.)

References

↑ M. Butler and M. Leuschel: Combining CSP and B for specification and property verification. FM 2005, LNCS 3582, Springer-Verlag, 2005 [1]

CSP-M Syntax

Details of supported CSP-M syntax

Note: you can use the command "Summary of CSP syntax" in ProB's help menu to get an up-to-date list of the supported syntax, along with current limitations.

PROCESS DEFINITIONS

`Process = ProcessExpression`

PROCESS EXPRESSIONS

`STOP` deadlocking process
`SKIP` terminating process
`CHAOS(a)` a: set of channel expressions
`ch->P` simple action prefix where ch is a channel name possibly followed by a sequence of outputs "!v" and input "?VAR", where v is a value expression and VAR a variable identifier
`ch?x:v->P` action prefix with set of accepted values
`P ; Q` sequential composition
`P ||| Q` interleaving
`P [] Q` external choice
`P |~| Q` internal choice
`P /\ Q` interrupt
`p [> Q` untimed timeout
`P [| a |] Q` parallel composition with synchronisation on set of channel expressions a
`P [ a || a' ] Q` alphabetised parallel
`P [ c<->c' ] Q` linked parallel
`P \ a` hiding of channel expressions in c
`P [[ c<-c' ]]` renaming of channels c into c'
`if B then P else Q`
`b & P` guard using a boolean expression b
`[]x:v@P` replicated external choice (x: variable, v: set value expression)
`|~|x:v@P` replicated internal choice (x: variable, v: set value expression)
`|||x:v@P` replicated interleave (x: variable, v: set value expression)
`;x:s@P` replicated sequential composition (s: sequence expression)
`||x:v@[a']P` replicated alphabetised parallel
`[| a |]x:s@P` replicated sharing
`[c<->c']x:s@P` replicated linked parallel (sequence s must be non empty)
`let f1=E1 ... fk=Ek within P`

BOOLEAN EXPRESSIONS

`true`
`false`
`b1 and b2` (`b1 && b2` also accepted but not in CSP-M)
`b1 or b2` (`b1 || b2` also accepted but not in CSP-M)
`b1 <=> b2` equivalence
`b1 => b2` implication
`not b`
`v==w` equality of values
`v!=w` disequality of values
`v<w,v>w` strict ordering
`v<=w,v>=w` non-strict ordering (v=<w also accepted)
`member(v,w)` set membership check
`empty(a)` set emptiness check
`null(s)` sequence emptiness check
`elem(x,s)` sequence member check

VALUE EXPRESSIONS

`v+w`, `v-w` addition and subtraction
`v*w` multiplication
`v/w` integer division
`v % w` division remainder
`bool(b)` convert a boolean expression into a boolean value
`{v,w,...}` enumerated sets
`{m..n}` closed range
`{m..}` open range
`union(v,w)` set union
`inter(v,w)` set intersection
`diff(v,w)` set difference
`Union(A)` generalized union of a set of sets
`Inter(A)` generalized intersection
`card(a)` cardinality of a
`{x1,...,xn | x<-a,b}`
`Events` all channel expressions on all declared channels
`{| ... |}` closure of set of channel expressions
`Set(a)` all subsets of a
`<>` empty sequence
`<v,w,...>` explicit sequence
`<m..n>` closed range sequence
`<m..>` open range sequence
`<....>^s` sequence concatenation (first or last arg has to be an explicit sequence for patterns)
`#s`, `length(s)`
`head(s)`
`tail(s)`
`concat(s)`
`set(s)` convert sequence into set

COMMENTS

`-- comment until end of line`
`{- arbitrary comment -}`

PRAGMAS

`transparent f` where f is a unary function which will then on be ignored by ProB
`{-# assert_ltl "f" "comment" #-}` where f is an LTL-formula and comment is an arbitrary comment, which is optional
`{-# assert_ctl "f" "comment" #-}` where f is a CTL-formula and comment is an arbitrary comment, which is optional

Checking CSP Assertions

As of version 1.3.4, ProB provides support for refinement checking and various other assertions (deadlock, divergence, determinism, and LTL/CTL assertions) of CSP-M specifications. In this tutorial we give a short overview of the ProB’s implementations and features for checking CSP assertions. In the Tcl/Tk interface of ProB, CSP assertions can be assembled and checked in the CSP Assertions Viewer. A description of the CSP Assertions Viewer is also given.

Supported CSP Assertions in ProB

ProB provides support for checking almost all types of CSP-M assertions that can be checked within FDR2. Besides the assertion types that can be checked in FDR2, in ProB one also can check temporal properties on processes expressed by means of LTL and CTL formulae.^[1] The following types of assertions are supported in ProB:

Refinement
Refinement is one of the fundamental notions for construction and verification of systems specified in CSP. Given two CSP processes P and Q one can state in ProB the property that process Q is an ‘m’ refinement of P by the following assertion declaration:

assert P [m= Q

where ‘m’ indicates one of the following types of comparison: ‘T’ for traces, ‘F’ for failures, ‘FD’ for failures-divergence, ‘R’ for refusals, and ‘RD’ for ‘refusals-divergence’. Note that the refinement types ‘V’ (revivals) and ‘VD’ (revivals-divergence) that are part of the refinement assertions supported by FDR2 are yet not supported by ProB.

Deadlock
Stating assertions about CSP processes to be deadlock-free is possible by the following assertion declaration:

assert P :[deadlock free [m]]

where P is a process expression and ‘m’ indicates one of the following models: ‘F’ (failures) and ‘FD’ (failures-divergence).

Determinism
Stating assertions about CSP processes to be deterministic is possible by the following assertion declaration:

assert P :[deterministic [m]]

where P is a process expression and ‘m’ one of the following models: ‘F’ (failures) and ‘FD’ (failures-divergence).

Livelock
Stating assertions about CSP processes to be livelock-free is possible by the following assertion declaration:

assert P :[livelock free]

where P is a process expression.

Temporal Properties
In ProB it is also possible to make assertions about temporal properties of CSP processes both in LTL and CTL. Basically, one wants to check whether some process P satisfies a formula f expressed in a temporal logic (denoted by P |= f).

To check whether a process P satisfies an LTL formula f write the following declaration:

assert P |= LTL: “f”

Note that f must be placed between quotes and that the satisfaction relation |= is immediately followed by `LTL:`. ProB supports LTL^[e], an extended version of LTL which provides additionally support for making propositions on transitions. The following LTL^[e] syntax for CSP-M specifications can be outlined by the following rules:

Atomic propositions:
- To check if an event `evt` is enabled in a state use `e(evt)`
Transition propositions:
- To check whether an event `evt` is executed use `[evt]`
Logical operators
- `true` and `false`
- `not`: negation
- `&`,`or` and `=>`: conjunction, disjunction and implication
Temporal operators:
- `G f`: globally
- `F f`: finally
- `X f`: next
- `f U g`: until
- `f W g`: weak-until
- `f R g`: release
Fairness operators:
- `WF(evt)` or `wf(evt)`: weak fairness, where `evt` is an event
- `SF(evt)` or `sf(evt)`: strong fairness, where `evt` is an event
- `WEF` and `SEF` for checking LTL^[e] formulae on executions that are strongly and weakly fair with respect to all events, respectively

An LTL^[e] formula f is satisfied by some CSP process P if all executions of P satisfy f. If there is an execution of P which violates the property f, then the test P |= f fails by providing a counterexample. Depending on whether f expresses, a safety or liveness property, a finite path or a path in a lasso-form (, i.e. a path leading to a cycle) is returned as a counterexample, respectively.

Note that ProB supports also Past-LTL^[e]. Past-LTL^[e], however, may be considered to be inappropriate for LTL assertions since the goal of this type of assertions is usually to check whether all executions starting at the initial states of the process satisfy the respective LTL^[e] formula.

To check whether a process P satisfies a CTL formula f the following assertion should be made:

assert P |= CTL: “f”

As for LTL, CTL formulae should be put in between quotes. The CTL syntax for CSP-M specifications could be summarised as follows:

Atomic propositions:
- To check if an event `evt` is enabled in a state use `e(evt)`
Transition propositions:
- To check whether an event `evt` is executed use `[evt]`
State formulae, where f, f1 and f2 are path formulae:
- true | false | `not` f | f1 `&` f2 | f1 `or` f2 | f1 `=>` f2,
- E f : path quantifier ` $\exists$ `, pronounced `for some path`
- A f : path quantifier ` $\forall$ `, pronounced `for all paths`
Path formulae, where g, g1 and g2 are state formulae:
- `X g`: next
- `g1 U g2`: until
- `G g`: globally
- `F g`: finally
Next executed event:
- `EX [e] true`:

Note that these two types of assertions, the LTL and CTL assertions, are not part of the CSP-M language supported by FDR2. Loading a CSP-M file in FDR2 having assertion declarations of this form will exit with a syntax error. Bear in mind to remove or comment out such LTL/CTL assertions in the CSP-M file before loading it in FDR2.

CSP Assertions Viewer

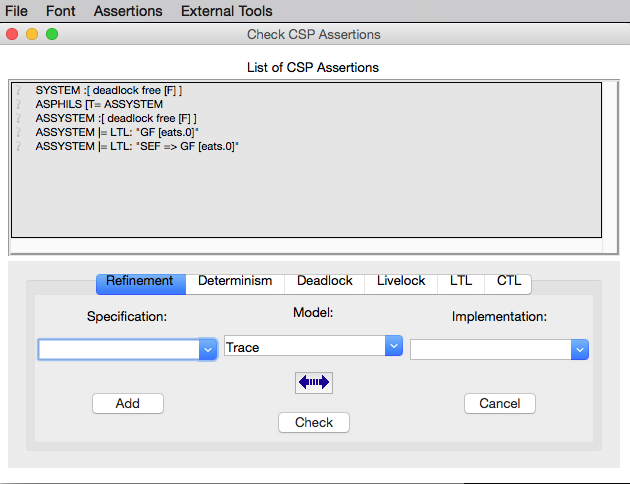
When a CSP-M specification is loaded one can open the CSP Assertion Viewer either from the menu bar of the main window by selecting the `Check CSP-M Assertions` command in the `Verify` menu or from the Refinement button in the ‘’State Properties’’ pane. The viewer looks as follows:

The CSP Assertion Viewer of ProB has a similar design to the graphical user interface of FDR2. It consists basically of three main components: a menu bar, a list box and a tab pane. In the following each of the components and their corresponding functionalities are thoroughly described.

The Menu Bar
The menu bar is placed at the top of the window. On OS X, it is placed at the top of the screen. The menu bar includes several menus providing commands for adjusting, executing and changing the items in the list box, as well as some (standard) options for re-loading the model, saving the items to an external file or the loaded file, and launching some external tools related with the domain in which the list items are checked. Each menu can be popped up by a click with Mouse-1 (usually the left mouse button). The menu bar consists of the following menus and menu commands:

File
- Reopen File: Reopening (re-reading and re-loading) the currently loaded file, incorporating any changes that may have been made since the file was last loaded.
- Copy new Assertions to File: All assertions that have been added to the list box since the currently loaded file was last read will be written to the file, i.e. all assertions that are yet not in the file are appended to it.
- Save Assertions to External File: Selecting the option opens a standard Tk dialog box requesting a name of a file in which the assertions and their results in the list box could be saved.
- Exit: Closing the CSP Assertion Viewer. Any assertion check results and any recently added assertions from the Tab Pane will get lost. The user will not be prompted to save these to the source file or an external file.
Font
Changing the font settings of the elements in the list box. Each of the items of this menu is a cascading menu that provides a number of options to be selected. The currently selected option in the cascading menu is marked by a tick symbol (✓).
- Family-Name: Change the font family of the text in the list box. There are currently four font families that could be chosen: Arial, Curier, Helvetica, and Times. Default font is Curier.
- Size: Change the font size of the text in the list box. Default font size is 10.
- Background: Change the background color of the list box. Default background color is Gray90.
Assertions
The menu provides a list of commands for checking different types of assertions. In case a particular type of assertions is checked the respective command checks only these assertions that are not checked yet.
- Uncheck All Assertions: Set the status of all assertions in the list box to non-checked (`?`).
- Delete All Assertions: Delete all assertions in the list box.
- Check All Refinement…: The item is a cascading menu and provides commands to check all assertions of one of the following supported refinement types: Traces, Failures, Failures-Divergence, Refusals, and Refusals-Divergence.
- Check Processes for…: The item is a cascading menu and provides commands to check all assertions of the following supported types of checks: Deadlock, Determinism and Livelock.
- Check All LTL Assertions: Selecting this command causes ProB to check all LTL assertions in the list box that are not checked yet.
- Check All CTL Assertions: Selecting this command causes ProB to check all CTL assertions in the list box that are not checked yet.
- Check All Assertions: Selecting this command causes ProB to check of all assertions in the list box that are not checked yet.
External Tools
- Open Specification with FDR: Open the currently loaded CSP-M specification in FDR2. The FDR2 tool is launched with the currently loaded specification in case the FDR2 is installed and the correct path to the `fdr2` command is set for the respective preference `Path to the FDR2 tool`. The value of the `Path to the FDR2 tool` preference can be changed from the “CSP Preferences…” window which can be opened by selecting the `CSP Preferences…` command in `Preferences` menu of the main window.
- Evaluate with CSPM-Interpreter: Selecting this command opens a console in which one can evaluate CSP-M expressions using the CSP-M interpreter. The CSP-M interpreter is an external tool implemented independently from ProB. CSP-M expression can be evaluated if the `cspm` tool is installed and the path to the cspm-command is set for the respective preference `Path to CSPM tool`. The command is obsolete and its removal is considered in future.

The Assertion List Box
This part of the viewer lists all assertions stated in the currently loaded CSP-M specification and provides a set of features for checking, manipulating, and debugging of CSP assertions in the list. To each statement in the assertion list box a symbol is assigned, placed on the left side of it, that reveals the current status of the statement in the viewer:

? - Assertion not checked yet.
✔ - Assertion check completed successfully.
✘ - Assertion check completed, but a counterexample was found to the stated property. The debugger can be used to explore the reason why the property does not hold.
⌚ - Assertion is currently checked.
! - The check of the assertion not completed for some reason. Possible causes for the interruption may be:
- Syntax error in the property was detected;
- Assertion check failed because of missing implementation;
- Assertion check interrupted by user.
  
  Note that in case of an LTL and a CTL assertion the check could fail to complete because of a syntax error in the respective formula. If an assertion check fails to complete an error box is popped up displaying an error message, which indicates why the assertion check could not be completed.

An assertion can be selected by clicking on it with Mouse-1 and checked by double-clicking on it with Mouse-1. Alternatively, selecting an assertion and then pressing the Enter key can start the respective assertion check. When an assertion check is in progress, the assertion will be marked by the clock symbol (⌚). If the assertion check is completed without interrupting it, a new status is assigned to the assertion: tick symbol (✔) indicating that the assertion was completed successfully or cross symbol (✘) indicating that a counterexample was found for the stated property. In case that the status is cross the counterexample can be explored by (second) double-click with Mouse-1 on the assertion or by selecting the assertion and then pressing the Enter key. If the respective assertion is negated, i.e. there is `not` in front of the assertion property, and marked with a cross, then no counterexample can be explored as the proper statement holds.

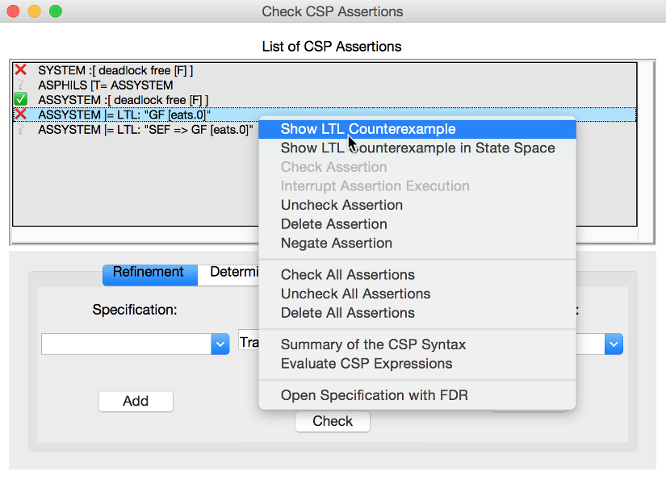
The list box is equipped with a contextual menu (or a pop-up menu), which appears when you right-click on an assertion in the list. Depending on the type and the status of the assertion the contextual menu provides options for checking, debugging, modifying the respective assertion, as well as various other options. Take, for example, the selected assertion on which the contextual menu is popped up in the picture below.

The assertion "ASSYSTEM |= LTL: “GF [eats.0]”" intends to check if the process ASSYSTEM satisfies the LTL formula "GF [eats.0]". For the selected assertion above, for example, the options `Show LTL Counterexample` and `Show LTL Counterexample in State Space` are enabled as a counterexample was found for the check. On the other hand, the options `Check Assertion` and `Interrupt Assertion` are disabled as the assertion check was completed.

The contextual menu has in general the following options:

The following options affect only the assertion being selected.

Debug or Show LTL/CTL Counterexample…: Opens the graphical viewer for exploring the counterexample that was found for the respective LTL assertion check. Option is enabled if the assertion is not negated and its status is cross (✘), or if the assertion is negated and its status is tick (✔). Option appears if the assertion type is an LTL assertion or a CTL assertion.
Debug Assertion: Opens a trace-failure debugger window showing the reason why the corresponding assertion check failed. Option is enabled if the assertion is not negated and its status is cross (✘), or if the assertion is negated and its status is tick (✔). Option available for all types of assertions except for LTL and CTL assertions.
Check Assertion: Starts immediately the check of the assertion being selected before right clicking on it.
Interrupt Assertion Check: Interrupts the current assertion check.
Uncheck Assertion: If the assertion was checked and the result of the check is different from question mark (?), then the status of the assertion will be reset to question mark. Option is enabled only if the assertion result is different from question mark.
Delete Assertion: Removes the selected item from the assertion list.
Negate Assertion: Negates the respective assertion. If the result of the (proper) assertion check is cross (✘), then the result of the negated assertion becomes tick (✔). Otherwise, if the result of the (proper) assertion is tick (✔), the negated assertion becomes cross (✘).
Swap Processes: Option available only for refinement assertions. Performing the command causes the attachment of a new refinement assertion in which the process expressions on both sides of the refinement operator `[m=` are swapped. If, for example, we execute ‘’Swap Processes’’ on the assertion "P [T= Q", the command adds to the list of assertions the assertion "Q [T= P".

The following options affect all assertions in the list box.

Check All Assertions: The command causes the check of all assertions in the list box. The assertions that are already checked would not be checked again.
Uncheck All Assertions: The status of all assertions in the list box is reset to question mark.
Delete All Assertions: All entries in the list box are removed. As a result the message “No assertions were added.” appears in the list box.

Other options. The following options have no impact on the assertions in the list box.

Summary of the CSP Syntax: Opens a window in which the summary of the CSP-M syntax and features supported by the ProB tool is given.
Evaluate CSP Expressions: Opens the Eval console in which CSP expressions can be evaluated.
Open Specification with FDR: Opens the currently loaded CSP-M specification in FDR2. The FDR2 tool is launched with the currently loaded specification if FDR2 is installed and the correct path to the `fdr2` command is set for the respective preference `Path to the FDR2 tool`. The value of the `Path to the FDR2 tool` preference can be changed from the “CSP Preferences…” window which can be opened by selecting the `CSP Preferences…` command in `Preferences` menu of the main window.

The Tab Pane

The tab pane is placed at the bottom of the window and enables the user to construct and check properties of processes of the currently loaded CSP-M file without adding explicitly assertions to the file.

There are overall six tab pages. Each tab page is used to build up new assertion statements. The tab pages provide selectors, entries and command buttons for assembling, adding and checking new assertions. In each of the selectors all possible processes of the loaded CSP-M file are accessible. It is also possible to specify new process expressions by entering these in the respective entry of the process selector. The tab pages for creating LTL and CTL assertions provide additionally an appropriate entry for specifying the according LTL and CTL formula intended to be checked on the specified process, respectively.

Each tab page is equipped with the following command buttons:

Add: Attaching a new assertion to the list of assertions in the list box. If the entry in one of the selectors is empty no assertion will be added to list box and a warning message will appear informing the user that some of the entries were not specified. If the entered assertion in the tab page is already in the list box, then a warning box appears informing the user that the assertion is already in the list box. If the assertion is present in the list box it will not be added.
Check: Attaching a new assertion to the list of assertions in the list box and immediately starting checking the assertion. If the assertion is already in the list box, then the user will be informed that the assertion is already in the list box and in case it is not checked yet its check will be started.
Cancel/Interrupt: Closes the window or interrupts an assertion check. In case the “Cancel” command is executed all checks and new assertions will get lost. If an assertion is currently checked, then the button command “Cancel” is replaced by another button command ‘’Interrupt’’, which causes the interruption of the current assertion check when the button is clicked on.

Debugging Non-satisfied Assertions

In case an assertion check has failed the user can explore the reason for the assertion violation. If the corresponding assertion is not negated and after finishing the assertion check is marked by cross, then this is an indication that ProB has found a counterexample for the check. The counterexample can be explored by a second double-click with the ‘Mouse-1’ button or by selecting the assertion and then pressing the ‘Enter’ button. Depending on the type of the assertion and the type of the counterexample a corresponding debugging window is opened.

If a CSP process violates an LTL formula or a universally quantified CTL formula, then by performing a second double-click on the respective assertion one can explore the provided counterexample by means of the graphical viewer (Graphical Viewer).

In the following we give an overview of the features for debugging counterexamples being found for different refinement checks. Consider the following CSP processes:

P = a -> b -> c -> STOP

Q = a -> (b -> Q [] c -> Q)

R = a -> b -> R

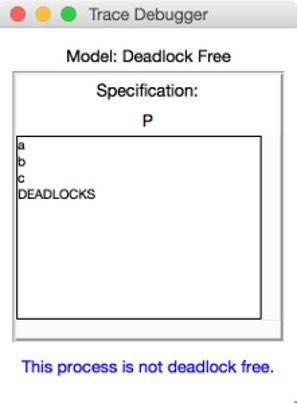
If we intend to check whether P is deadlock free, then we can state the assertion

assert P :[deadlock free [F]].

The check of the assertion will finish by marking the assertion in the list box with a cross symbol (✘). The cross symbol indicates that a counterexample was found for the assertion check. The counterexample is basically given by the trace $\langle a,b,c\rangle$ as obviously `P` reaches a deadlock state after performing the trace $\langle a,b,c\rangle$ . Providing a second double-click on the assertion will open the following debugging window:

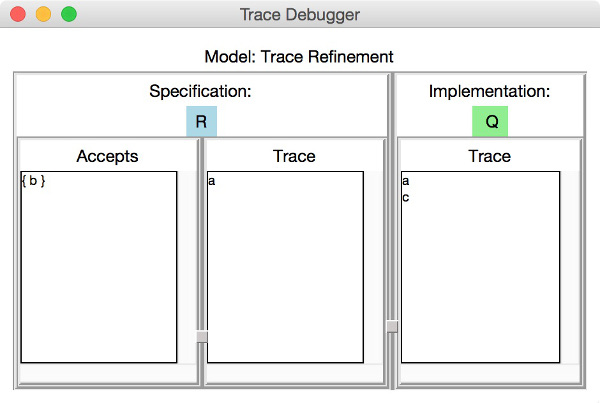
Considering the CSP processes `Q` and `R` one can see or check that `R` is a trace refinement of `Q` since `R` performs the same set of traces as `Q`. Thus, the assertion check for `Q [T= R` will mark the assertion statement in the list box by a tick symbol (✔). On the other hand, checking the assertion `R [T= Q` will find a counterexample for the refinement check. Performing a second double-click on the item `R [T= Q` will open the following trace debugger window with the counterexample displayed in it:

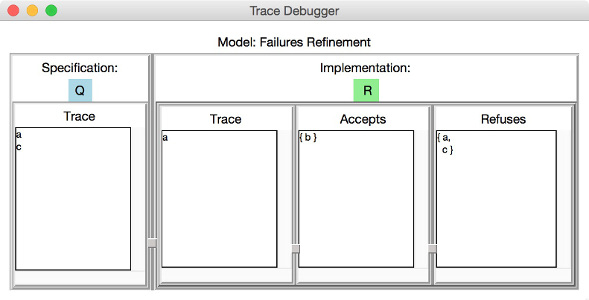
A counterexample of a trace-refinement assertion is a trace leading to a state in which the implementation process performs an event that the specification process cannot perform. In the example above both processes `P` and `Q` perform the trace $\langle a\rangle$ and reach states in which the implementation process can perform an event that is not offered by the specification process R. One can easily deduce from the picture above that `Q` performs after `a` the event `c` which is not offered by `R` as `R` can perform only `b` after `a`. In the left most column `Accept` the debugger window lists all possible events that are offered by the specification process after performing the trace given in the `Trace` column next to `Accepts`.

As we already mentioned above `R` is a trace-refinement of `Q`. On the other hand, checking whether `R` is a failures-refinement of `Q` will produce a counterexample since `R` refuses the event `c` that is offered by Q after executing `a`. Accordingly, the counterexample will be illustrated within the following trace debugger window:

These are basically the three types of debugging windows that will appear when debugging a counterexample for an assertion check in case the respective assertion is not an LTL or a CTL assertion. When a counterexample for an LTL assertion is found it will be explored in the graphical viewer, the same graphical viewer that is used for visualizing the state space models in ProB.

Let us observe again the CSP process `Q` and suppose we want to check whether `Q` satisfies the LTL formula `F [c]`. Then, the respective LTL assertion is declared as follows:

assert Q |= LTL: “F [c]”

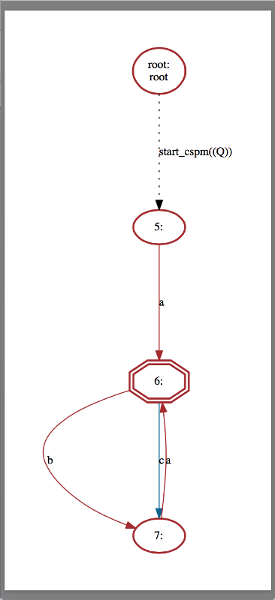
The assertion check will produce a counterexample as `Q` obviously reaches a cycle “(b -> a)+” that violates the property “F [c]”. Performing a second double-click on the assertion will display the following state space graph in the graphical viewer:

In the figure above, the nodes and the transitions of the respective counterexample "a -> (b -> a)+" are colored in red.

Checking CSP Assertions with `probcli`

It is also possible to check CSP assertions with the command line version of ProB. The command has the following syntax:

probcli -csp_assertion "A" File

where A is a CSP assertion and File the path to the CSP file. For example, if we want to check the refinement assertion `P [T= Q` on some CSP specification `example.csp`, then we can do this by running the ProB command line version with the following options:

probcli -csp_assertion "P [T= Q" example.csp

Note that the assertion should be placed between quotes. In addition, when an assertion is checked with the '-csp_assertion' option the keyword assert should be omitted.

Notice that for checking LTL and CTL assertions from the command line you need to escape the double quotes (") wrapping the respective LTL/CTL formula by means of a backslash \.

probcli -csp_assertion "Q |= LTL: \"F [c]\"" example.csp

References and Notes

↑ ProB provides support for LTL and CTL model checking (citations needed).

Alloy

As of version 1.8 ProB provides support to load Alloy models. The Alloy models are translated to B machines by a Java frontend.

This work and web page is still experimental.

The work is based on a translation of the specification language Alloy to classical B. The translation allows us to load Alloy models into ProB in order to find solutions to the model's constraints. The translation is syntax-directed and closely follows the Alloy grammar. Each Alloy construct is translated into a semantically equivalent component of the B language. In addition to basic Alloy constructs, our approach supports integers and orderings.

Installation

Alloy2B is included as of version 1.8.2 of ProB.

You can build Alloy2B yourself:

Clone or download Alloy2B project on Github.
Make jar file (gradle build) and
put resulting alloy2b-*.jar file into ProB's lib folder.

Examples

N-Queens

module queens
open util/integer
sig queen { x:Int, x':Int, y:Int } {
    x >= 1
    y >= 1
    x <= #queen
    y <= #queen
    x' >=1
    x' <= #queen
    x' = minus[plus[#queen,1],x]
}
fact { all q:queen, q':(queen-q) {
    ! q.x = q'.x
    ! q.y = q'.y
    ! plus[q.x,q.y] = plus[q'.x,q'.y]
    ! plus[q.x',q.y] = plus[q'.x',q'.y]
}}
pred show {}
run show for exactly 4 queen, 5 int

This can be loaded in ProB, as shown in the following screenshot. To run the "show" command you have to use "Find Sequence..." command for "run_show" in the "Constraint-Based Checking" submenu of the "Verify" menu.

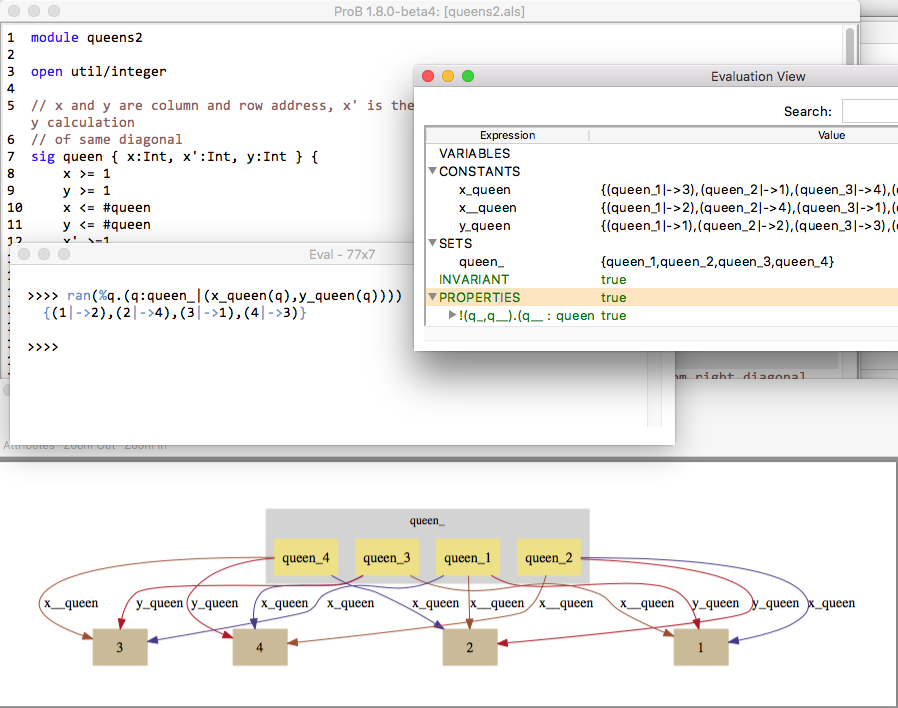
Internally the Alloy model is translated to the following B model:

MACHINE alloytranslation
SETS /* deferred */
  queen
CONCRETE_CONSTANTS
  x,
  x_,
  y
/* PROMOTED OPERATIONS
  run0 */
PROPERTIES
    x : queen --> INTEGER
  & x_ : queen --> INTEGER
  & y : queen --> INTEGER
  & !this.(this : queen => x(this) >= 1 & y(this) >= 1 & x(this) <= card(queen) & y(this) <= 
  card(queen) & x_(this) >= 1 & x_(this) <= card(queen) & x_(this) = (card(queen) + 1) - x(this)
  )
  & card(queen) = 4
  & !(q,q_).(q_ : queen - {q} => not(x(q) = x(q_)) & not(y(q) = y(q_)) & not(x(q) + y(q) = x(
  q_) + y(q_)) & not(x_(q) + y(q) = x_(q_) + y(q_)))
INITIALISATION
    skip
OPERATIONS
  run0 = 
    PRE 
        card(queen) = 4
      & !(q,q_).(q_ : queen - {q} => not(x(q) = x(q_)) & not(y(q) = y(q_)) & not(x(q) + y(q)
   = x(q_) + y(q_)) & not(x_(q) + y(q) = x_(q_) + y(q_)))
    THEN
      skip
    END
/* DEFINITIONS
  PREDICATE show; */
END

River Crossing Puzzle

module river_crossing
open util/ordering[State]
abstract sig Object { eats: set Object }
one sig Farmer, Fox, Chicken, Grain extends Object {}
fact { eats = Fox->Chicken + Chicken->Grain}
sig State { near, far: set Object }
fact { first.near = Object && no first.far }
pred crossRiver [from, from', to, to': set Object] {
  one x: from | {
    from' = from - x - Farmer - from'.eats
    to' = to + x + Farmer
  }
}
fact {
  all s: State, s': s.next {
    Farmer in s.near =>
      crossRiver [s.near, s'.near, s.far, s'.far]
    else
      crossRiver [s.far, s'.far, s.near, s'.near]
  }
}
run { last.far=Object } for exactly 8 State

This can be loaded in ProB, as shown in the following screenshot. To run the "show" command you have to use "Find Sequence..." command for "run_show" in the "Constraint-Based Checking" submenu of the "Verify" menu (after enabling Kodkod in the Preferences menu).

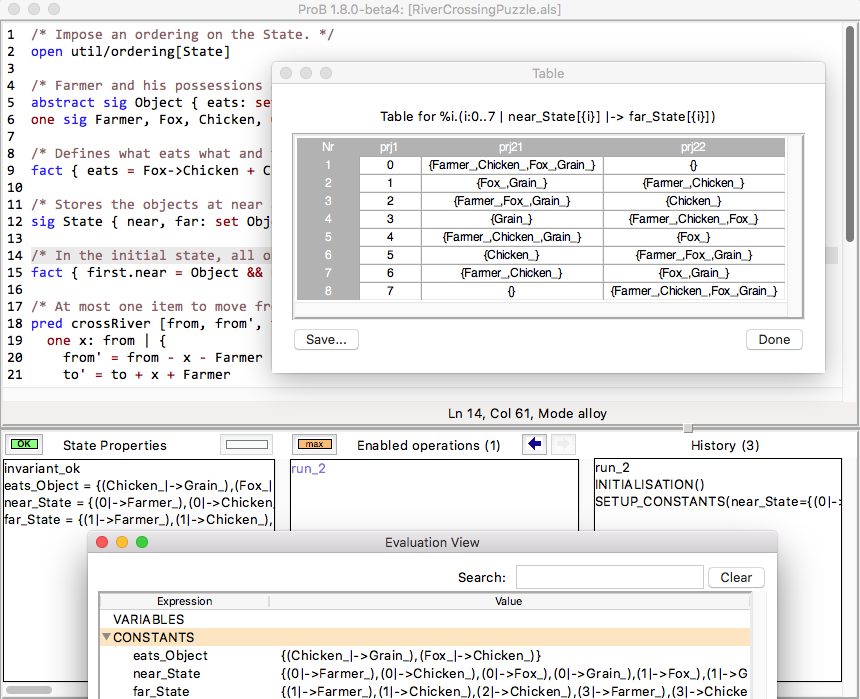
Internally the Alloy model is translated to the following B model:

/*@ generated */
MACHINE river_crossing
SETS
    Object_
CONSTANTS
    Farmer_, Fox_, Chicken_, Grain_, eats_Object, near_State, far_State
DEFINITIONS
    crossRiver_(from_,from__,to_,to__) == from_ <: Object_ 
    									  & from__ <: Object_ & to_ <: Object_ 
    									  & to__ <: Object_  &  (card({x_ | {x_} <: from_
    									  & (((from__ = (((from_ - {x_}) - {Farmer_}) - eats_Object[from__])))
    									  & ((to__ = ((to_ \/ {x_}) \/ {Farmer_}))))}) = 1) ;
    next_State_(s) == {x|x=s+1 & x:State_} ;
    nexts_State_(s) == {x|x>s & x:State_} ;
    prev_State_(s) == {x|x=s-1 & x:State_} ;
    prevs_State_(s) == {x|x<s & x:State_} ;
    State_ == 0..7
PROPERTIES
    {Farmer_} <: Object_ &
    {Fox_} <: Object_ &
    {Chicken_} <: Object_ &
    {Grain_} <: Object_ &
    ((eats_Object = (({Fox_} * {Chicken_}) \/ ({Chicken_} * {Grain_})))) &
    (((near_State[{min(State_)}] = Object_) & far_State[{min(State_)}] = {})) &
    (!(s_, s__).({s_} <: State_ & {s__} <: next_State_(s_) => 
    			((({Farmer_} <: near_State[{s_}]) => 
    					crossRiver_(near_State[{s_}], near_State[{s__}],
    					 far_State[{s_}], far_State[{s__}])) 
    					& (not(({Farmer_} <: near_State[{s_}])) =>
    							 crossRiver_(far_State[{s_}], far_State[{s__}],
    							  near_State[{s_}], near_State[{s__}]))))) &
    Farmer_ /= Fox_ &
    Farmer_ /= Chicken_ &
    Farmer_ /= Grain_ &
    Fox_ /= Chicken_ &
    Fox_ /= Grain_ &
    Chicken_ /= Grain_ &
    {Farmer_} \/ {Fox_} \/ {Chicken_} \/ {Grain_} = Object_ &
    eats_Object : Object_ <-> Object_ &
    near_State : State_ <-> Object_ &
    far_State : State_ <-> Object_
OPERATIONS
    run_2 = PRE (far_State[{max(State_)}] = Object_) THEN skip END
END

Proof with Atelier-B Example

sig Object {}
sig Vars {
    src,dst : Object
}
pred move (v, v': Vars, n: Object) {
    v.src+v.dst = Object
    n in v.src
    v'.src = v.src - n
    v'.dst = v.dst + n
	}
assert add_preserves_inv {
    all v, v': Vars, n: Object |
         move [v,v',n] implies  v'.src+v'.dst = Object
}
check add_preserves_inv for 3

Note that our translation does not (yet) generate an idiomatic B encoding, with move as B operation

and src+dst=Object as invariant: it generates a check operation encoding the predicate
 add_preserves_inv
 with universal quantification.

Below we shoe the B machine we have input into AtelierB. It was obtained by pretty-printing from \prob, and putting the negated guard

of theadd_preserves_inv into an assertion (so that AtelierB generates the desired proof obligation).

MACHINE alloytranslation
SETS /* deferred */
  Object_; Vars_
CONCRETE_CONSTANTS
  src_Vars, dst_Vars
PROPERTIES
    src_Vars : Vars_ --> Object_
  & dst_Vars : Vars_ --> Object_
ASSERTIONS
  !(v_,v__,n_).(v_ : Vars_ & v__ : Vars_ & n_ : Object_
   => 
   (src_Vars[{v_}] \/ dst_Vars[{v_}] = Object_ & 
    v_ |-> n_ : src_Vars &
    src_Vars[{v__}] = src_Vars[{v_}] - {n_} &
    dst_Vars[{v__}] = dst_Vars[{v_}] \/ {n_} 
    =>
    src_Vars[{v__}] \/ dst_Vars[{v__}] = Object_)
   )
END

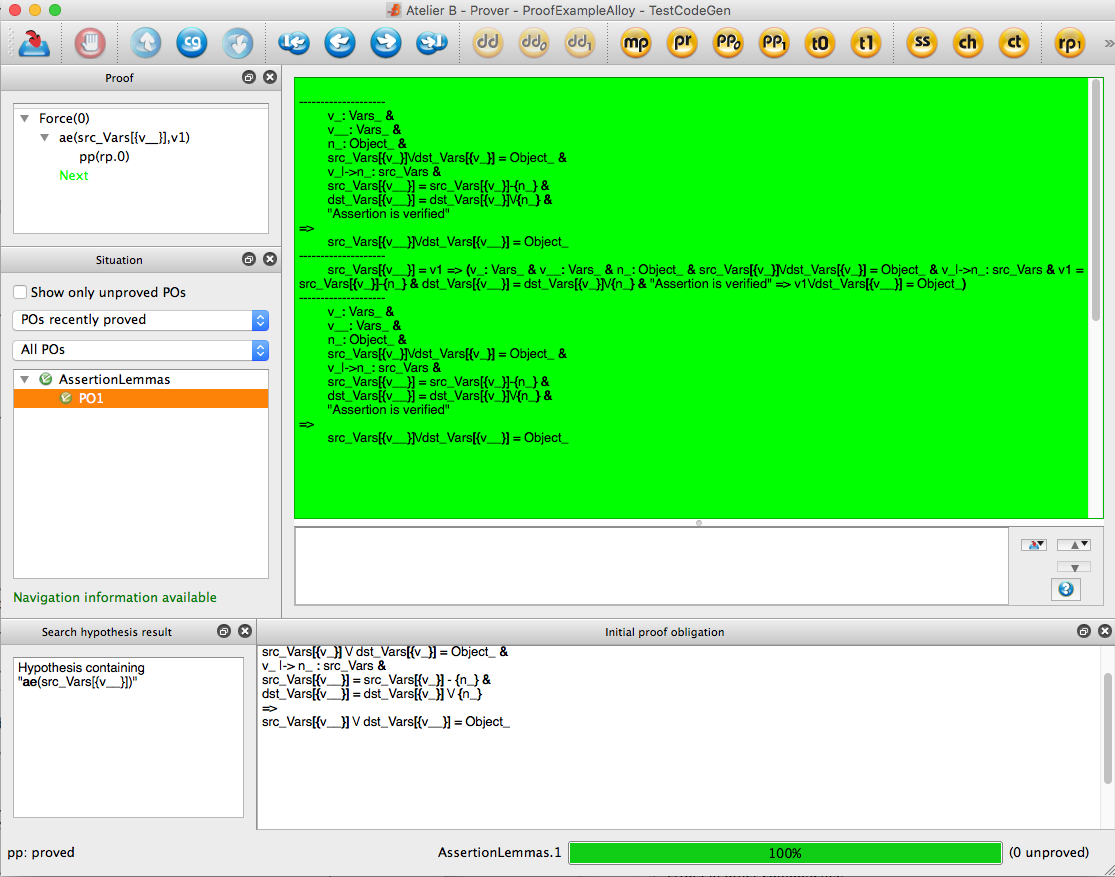
The following shows AtelierB proving the above assertion:

Alloy Syntax

Logical predicates:
-------------------
 P and Q       conjunction
 P or Q        disjunction
 P implies Q   implication
 P iff Q       equivalence
 not P         negation

Alternative syntax:
 P && Q        conjunction
 P || Q        disjunction
 P => Q        implication
 P <=> Q       equivalence
 ! P           negation

Quantifiers:
-------------
 all DECL | P   universal quantification
 some DECL | P  existential quantification
 one DECL | P   existential quantification with exactly one solution
 lone DECL | P  quantification with one or zero solutions

where the DECL follow the following form:
 x : S          choose a singleton subset of S (like x : one S)
 x : one S      choose a singleton subset of S
 x : S          choose x to be any subset of S
 x : some S     choose x to be any non-empty subset of S
 x : lone S     choose x to be empty or a singleton subset of S
 x : Rel        where Rel is a cartesian product / relation: see multiplicity declarations x in Rel
 x,y... : S, v,w,... : T  means x:S and y : S and ... v:T and w:T and ...
 disjoint x,y,... : S     means x : S and y : S and ... and x,y,... are all pairwise distinct

Set Expressions:
----------------
 univ           all objects
 none           empty set
 S + T          set union
 S & T          set intersection
 S - T          set difference
 # S      cardinality of set

Set Predicates:
---------------
 no S           set S is empty
 S in T         R is subset of S
 S = T          set equality
 S != T         set inequality
 some S         set S is not empty
 one S          S is singleton set
 lone S         S is empty or a singleton
 {x:S | P}      set comprehension
 {DECL | P}     set comprehension, DECL has same format as for quantifiers
 let s : S | P  identifier definition

Relation Expressions:
----------------------
 R -> S         Cartesian product
 R . S          relational join
 S <: R         domain restriction of relation R for unary set S
 R :> S         range restriction of relation R for unary set S
 R ++ Q         override of relation R by relation Q
 ~R             relational inverse
 ^R             transitive closure of binary relation
 *R             reflexive and transitive closure

Multiplicity Declarations:
---------------------------
The following multiplicity annotations are supported for binary (sub)-relations:

 f in S -> T            f is any relation from S to T (subset of cartesian product)
 f in S -> lone T       f is a partial function from S to T
 f in S -> one T        f is a total function from S to T
 f in S -> some T       f is a total relation from S to T
 f in S one -> one T    f is a total bijection from S to T
 f in S lone -> lone T  f is a partial injection from S to T
 f in S lone -> one T   f is a total injection from S to T
 f in S some -> lone T  f is a partial surjection from S to T
 f in S some -> one T   f is a total surjection from S to T
 f in S some -> T       f is a surjective relation from S to T
 f in S some -> some T  f is a total surjective relation from S to T

Ordered Signatures:
-------------------
A signature S can be defined to be ordered:
 open util/ordering [S] as s

 s/first            first element
 s/last             last element
 s/max              returns the largest element in s or the empty set
 s/min              returns the smallest element in s or the empty set
 s/next[s2]         element after s2
 s/nexts[s2]        all elements after s2
 s/prev[s2]         element before s2
 s/prevs[s2]        all elements before s2
 s/smaller[e1,e2]   return the element with the smaller index
 s/larger[e1,e2]    returns the element with the larger index
 s/lt[e1,e2]        true if index(e1) < index(e2)
 s/lte[s2]          true if index(e1) =< index(e2)
 s/gt[s2]           true if index(e1) > index(e2)
 s/gte[s2]          true if index(e1) >= index(e2)

Sequences:
----------
The longest allowed sequence length (maxseq) is set in the scope of a run or check command using the 'seq' keyword.
Otherwise, a default value is used.
The elements of a sequence s are enumerated from 0 to #s-1.

 s : seq S       ordered and indexed sequence
 #s              the cardinality of s
 s.isEmpty       true if s is empty
 s.hasDups       true if s contains duplicate elements
 s.first         head element
 s.last          last element
 s.butlast       s without its last element
 s.rest          tail of the sequence
 s.inds          the set {0,..,#s-1} if s is not empty, otherwise the empty set
 s.lastIdx       #s-1 if s is not empty, otherwise the empty set
 s.afterLastIdx  #s if s is smaller than maxseq, otherwise the empty set
 s.idxOf [x]     the first index of the occurence of x in s, the empty set if x does not occur in s
 s.add[x]        insert x at index position i
 s.indsOf[i]     the set of indices where x occurs in s, the empty set if x does not occur in s
 s.delete[i]     delete the element at index i
 s.lastIdxOf[x]  the last index of the occurence of x in s, the empty set if x does not occur in s
 s.append[s2]    concatenate s and s2, truncate the result if it contains more than maxseq elements
 s.insert[i,x]   insert x at index position i, remove the last element if #s = maxseq
 s.setAt[i,x]    replace the value at index position i with x
 s.subseq[i,j]   the subsequence of s from indices i to j inclusively

[see http://alloy.lcs.mit.edu/alloy/documentation/quickguide/seq.html]

Arithmetic Expressions and Predicates:
--------------------------------------
You need to open util/integer:

 plus[X,Y]       addition
 minus[X,Y]      subtraction
 mul[X,Y]        multiplication
 div[X,Y]        division
 rem[X,Y]        remainder
 sum[S]          sum of integers of set S

 X < Y           less
 X = Y           integer equality
 X != Y          integer inequality
 X > Y           greater
 X =< Y          less or equal
 X >= Y          greater or equal

Structuring:
------------
fact NAME { PRED }
fact NAME (x1,...,xk : Set) { PRED }

pred NAME { PRED }
pred NAME (x1,...,xk : Set) { PRED }

assert NAME { PRED }

fun NAME : Type { EXPR }

Commands:
---------

run NAME
check NAME

run NAME for x                      global scope of less or equal x
run NAME for exactly x1 but x2 S    global scope of x1 but less or equal x2 S
run NAME for x1 S1,...,xk Sk        individual scopes for signatures S1,..,Sk
run NAME for x Int                  specify the integer bitwidth (integer overflows might occur)
run NAME for x seq                  specify the longest allowed sequence length

TLA

As of version 1.3.5, ProB supports TLA+.

Using ProB for Animation and Model Checking of TLA+ specifications

The latest version of ProB uses the translator TLA2B, which translates the non temporal part of a TLA+ module to a B machine. To use ProB for TLA+ you have to download the TLA tools. They are released as an open source project, under the MIT License. In the ProB Tcl/Tk GUI you have to select the menu command "Download and Install TLA Tools" in the Help menu.

When you open a TLA+ module ProB generates the translated B machine in the same folder and loads it in the background. If there is a valid translation you can animate and model check the TLA+ specification. There are many working examples in the 'ProB/Examples/TLA+/'-directory.

There is also an iFM'2012 paper that describes our approach and performs some comparison with TLC. Our online ProB Logic Calculator now also supports TLA syntax and you can experiment with its predicate and expression evaluation capabilities.

TLA2B

The parser and semantic analyzer SANY serves as the front end of TLA2B. SANY was written by Jean-Charles Grégoire and David Jefferson and is also the front end of the model checker TLC. After parsing there is type checking phase, in which types of variables and constants are inferred. So there is no need to especially declare types in a invariant clause (in the manner of the B method). Moreover it checks if a TLA+ module is translatable (see Limitations of Translation).

To tell TLA2B the name of a specification of a TLA+ module you can use a configuration file, just like for TLC. The configuration file must have the same name as the name of the module and the filename extension 'cfg'. The configuration file parser is the same as for TLC so you can look up the syntax in the 'Specifying Systems'-book (Leslie Lamport). If there is no configuration file available TLA2B looks for a TLA+ definition named 'Spec' or alternatively for a 'Init' and a 'Next' definition describing the initial state and the next state relation. Besides that in the configuration file you can give a constant a value but this is not mandatory, in contrast to TLC. Otherwise ProB lets you choose during the animation process a value for the constant which satisfy the assumptions under the ASSUME clause. TLA2B supports furthermore overriding of a constant or definition by another definition in the configuration file.

Supported TLA+ syntax

Logic
-----
 P /\ Q                       conjunction
 P \/ Q                       disjunction
 ~ or \lnot or \neg           negation
 =>                           implication
 <=> or \equiv                equivalence
 TRUE
 FALSE
 BOOLEAN                      set containing TRUE and FALSE
 \A x \in S : P               universal quantification
 \E x \in S : P               existential quantification
 
Equality:
------
 e = f                        equality
 e # f or e /= f              inequality 

Sets
------
 {d, e}                       set consisting of elements d, e
 {x \in S : P}                set of elements x in S satisfying p
 {e : x \in S}                set of elements e such that x in S
 e \in S                      element of
 e \notin S                   not element of
 S \cup T or S \union T       set union
 S \cap T or S \intersect     set intersection
 S \subseteq T                equality or subset of
 S \ t                        set difference
 SUBSET S                     set of subsets of S
 UNION S                      union of all elements of S

Functions
------
 f[e]                         function application
 DOMAIN f                     domain of function f
 [x \in S |-> e]              function f such that f[x] = e for x in S
 [S -> T]                     Set of functions f with f[x] in T for x in S
 [f EXCEPT ![e] = d]          the function equal to f except f[e] = d

Records
-------
 r.id                         the id-field of record r
 [id_1|->e_1,...,id_n|->e_n]  construct a record with given field names and values
 [id_1:S_1,...,id_n:S_n]      set of records with given fields and field types
 [r EXCEPT !.id = e]          the record equal to r except r.id = e

Strings and Numbers
-------------------
 "abc"                        a string
 STRING                       set of a strings
 123                          a number
 
Miscellaneous constructs
------------------------
IF P THEN e_1 ELSE e_2
CASE P_1 -> e_1 [] ... [] P_n ->e_n
CASE P_1 -> e_1 [] ... [] P_n ->e_n [] OTHER -> e
LET d_1 == e_1 ... d_n == e_n IN e

Action Operators
----------------
v'                            prime operator (only variables are able to be primed)
UNCHANGED v                   v'=v
UNCHANGED <<v_1, v_2>>        v_1'=v_1 /\ v_2=v_2

Supported standard modules
--------------------------
Naturals
--------
x + y                         addition
x - y                         difference
x * y                         multiplication
x \div y                      division
x % y                         remainder of division
x ^ y                         exponentiation
x > y                         greater than
x < y                         less than
x \geq y                      greater than or equal
x \leq y                      less than or equal
x .. y                        set of numbers from x to y
Nat                           set of natural numbers

Integers
--------
-x                            unary minus
Int                           set of integers

Sequences
---------
SubSeq(s,m,n)                 subsequence of s from component m to n
Append(s, e)                  appending e to sequence s
Len(s)                        length of sequence s
Seq(s)                        set of sequences
s_1 \o s_2 or s_1 \circ s_2   concatenation of s_1 and s_2
Head(s)
Tail(s)

FiniteSets
----------
Cardinality(S)
IsFiniteSet(S)                (ProB can only handle certain infinite sets as argument) 



typical structure of a TLA+ module
--------------------------

---- MODULE m ----
EXTENDS m_1, m_2
CONSTANTS c_1, c_2
ASSUME c_1 = ...
VARIABLES v_1, v_2
foo == ...
Init == ...
Next == ...
Spec == ...
=====================

Temporal formulas and unused definitions are ignored by TLA2B (they are also ignored by the type inference algorithm).

Limitations of the translation

due to the strict type system of the B method there are several restrictions to TLA+ modules.
- the elements of a set must have the same type (domain and range of a function are sets)
- TLA+ tuples are translated as sequences in B, hence all components of the tuple must have the same type
TLA2B do not support 2nd-order operators, i.e. operators that take a operator with arguments as argument (e.g.: foo(bar(_),p))

TLA+ Actions

TLA2B divides the next state relation into different actions if a disjunction occurs. IF a existential quantification occurs TLA2B searches for further actions in the predicate of the quantification and adds the bounded variables as arguments to these actions. IF a definition call occurs and the definition has no arguments TLA2B goes into the definition searching for further actions. The displayed actions by ProB are not necessarily identical with the actions determined by TLC.

Understanding the type checker

Corresponding B types to TLA+ data values (let type(e) be the type of the expression e):

TLA+ data                               B Type
--------------------------------------------------
number e.g. 123                         INTEGER
string e.g. "abc"                       STRING
bool value e.g. TRUE                    BOOL
set e.g. {e,f}                          POW(type(e)), type(e) = type(f)
function e.g. [x \in S |-> e]           POW(type(x)*type(e)), type(S) = POW(type(x))
sequence e.g. <<a,b>>                   POW(INTEGER*type(a)), type(a) = type(b)
record e.g. [id_1|->e_1,...,id_n|->e_n] struct(id_1:type(e_1),...,id_n:type(e_n))
model value                             ENUM 
 (only definable in config file)

Nat                                     POW(INTEGER)
Int                                     POW(INTEGER)
STRING                                  POW(STRING)
BOOLEAN                                 POW(BOOL)
SUBSET S                                POW(type(S))

You can only compare data values with the same type.

ProZ

ProZ is a extension of the ProB animator and model checker to support Z specifications. It uses the Fuzz Type Checker by Mike Spivey for extracting the formal specification from a LaTeX file. On the website you can also find documentation about the syntax of Z specifications. The iFM'07 article on ProZ contains more details about the implementation.

Preferences

A Z specification frequently makes use of comprehension sets, which are often introduced by the underlying translation process from Z to B. Normally those comprehension sets should be treated symbolically. To support this, you should set the following in the preferences menu:

Animation Preferences ->
 - Lazy expansion of lambdas & set comprehensions: True
 - Convert lazy form back into explicit form for Variables and Constants: False

Structure of the Z Specification

State and Initialization

To identify the components (like state, initialization, operations) of a Z specification, ProZ expects a certain structure of the specification: There must be a schema called "Init". "Init" describes the initialization of the state. "Init" must include exactly one schema in the declaration part. This schema is assumed to be the state schema.

For example, let S be the state schema (= is used for \defs):

 S = [ x,y:N ]

There are two supported styles for the initialization:

a)   Init = [ S | x=0 /\ y=1]

b)   Init = [ S'| x'=0 /\ y'=1 ]

If you want to use the logic of other schemas besides the state schema in the initialization, you can do that by including those schemas in the predicate part.

Operations

ProZ identifies schemas as operations if they satisfy the following properties:

All variables of the state and their primed counterpart are declared in the operation. Usually this is done by including "\Delta S" in the operation (with S being the state schema).
The operation is not referenced by any other schema in the specification

Example: Let S be defined as above:

 A = [ \Delta S | x'=x+1 /\ y'=y ]
 B = [ x,y,x',y':N | x'=x+1 /\ y'=y ]
 C = [ x,x':N | x'=x+1 ]
 D = [ y,y':N | y'=y ]
 E = C /\ D
 F = [ \Xi S | x=0 ]

Then the schemas A,B and E describe all the same operation. F is also identified as an operation that leaves the state unchanged.

Axiomatic definitions

If axiomatic definitions are present, the declared variables are treated like constants. In the first step of the animation, ProB searches for values that satisfy all predicates of the axiomatic definitions are searched. After the first step, the predicates of the axiomatic definitions are ignored. If you want to define functions in an axiomatic definition, consider that ProB can treat lambda expressions and set comprehensions symbolically. Example: The definition of a function "square" could be

a)

| square : Z -> Z
|-----------------------
| square = (\lambda x:Z @ x*x)

b)

| square : Z -> Z
|-----------------------
| \forall x:Z @ square x = x*x

When using ProZ, it is preferable to use the method "a" because the lambda expression can be interpreted symbolically. If "b" is used, ProB will try to find a explicit set that will satisfy the given property.

Invariant

You can add a B-style invariant to the specification by defining a schema "Invariant" that declares a subset of the state variables. In each explored state the invariant will be checked. The model checking feature of ProB will try to find states that violate the invariant.

Scope

It is possible to limit the search space of the model checker by adding a schema "Scope" that declares a subset of the state variables. If such a schema is present, each explored state is checked, if it satisfies the predicate. If not, the state is not further explored.

Abbreviation Definitions

Abbreviation definitions (e.g. Abbr == {1,2,3}) are used like macros by ProZ. A reference to an abbreviation is replaced by its definition in a preprocessor phase. Thereby schemas defined by abbreviation definitions are ignored when ProZ tries to identify components. So, it is recommended to use schema definitions instead of abbreviation definitions (\defs instead of ==) when defining state, initialization, operations, etc.

Graphical animation

(Please note that this functionality is part of the next version. If you want to use graphical animation, please download a version from the Nightly build.)

Analogous to the graphical animation for B specifications, you can define a function that maps a coordinate to an image. Then ProZ will display the grid of images while animating the specification.

To use this feature, add a schema Proz_Settings that contains a variable animation\_function. The animation function should map a coordinate to an image. A coordinate is a pair of numbers or given sets.

The type used for images must be an enumerated set where the names of the elements denote their file names (without the suffix .gif).

Please see the specification jars.tex which is bundled with the ProB Tcl/Tk version for Download (inside the examples/Z/GraphicalAnimation/ directory). This is the part of the specification that defines the animation function (actually it defines a pair of animation functions: the default function over which the other function is overlaid; see Graphical_Visualization for more details):

We declare a type for the used images, the names of the elements refer to the file names of the GIF files.
\begin{zed}
 Images ::= Filled | Empty | Void
\end{zed}
The animation consists of a grid of images that is updated in each new state.
The $animation\_function$ maps a coordinate to an image where $(1\mapsto 1)$ is the upper-left corner.
\begin{schema}{ProZ\_Settings}
 Level \\
 animation\_function\_default : (\nat \cross Jars) \pfun Images \\
 animation\_function : (\nat \cross Jars) \pfun Images \\
 \where
 animation\_function\_default = (1\upto global\_maximum \cross Jars) \cross \{ Void \} \\
 animation\_function = \\
 \t1 (\{ l:1\upto global\_maximum; c:Jars | l\leq max\_fill~c @ \\
 \t2 global\_maximum+1-l\mapsto c\} \cross \{Empty\}) \oplus \\
 \t1 (\{ l:1\upto global\_maximum; c:Jars | l\leq level~c @ \\
 \t2 global\_maximum+1-l\mapsto c\} \cross \{Filled\})
\end{schema}

Here is how the animation of the specification should look like:

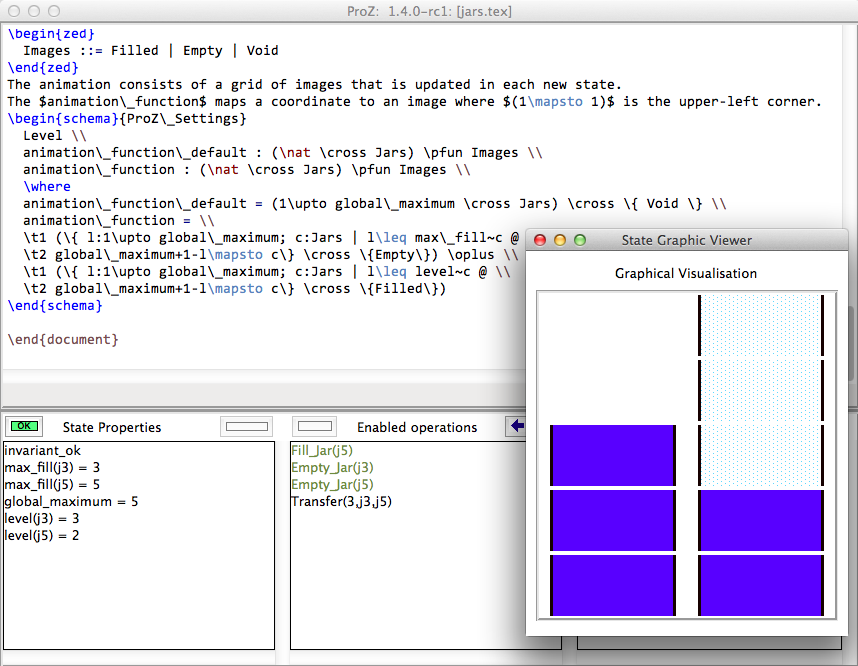
Special constructs

prozignore

Sometimes it is not desired to check properties of some variables. E.g. ProZ checks if the square function in 2.3.a is a total function by enumerating it (it checks the function only for a limited interval). For more complex definitions the number of entries is often too large to check. When the user is sure that those properties are satisfied (like in our example), a solution is relaxing the declaration from "square : Z -> Z" to "square : Z <-> Z". Sometimes this is not easy to do, for instance if schema types are used which imply other constraints.

ProZ supports an operation \prozignore that instructs ProZ to ignore all constraints on the type and to use just the underlying type. For example, the square function could be defined by:

| square : \prozignore( Z -> Z )
|-----------------------
| square = (\lambda x:Z @ x*x)

If you want to use \prozignore, you must first define a TeX command \prozignore:

\newcommand{\prozignore}{ignore_\textsl{\tiny ProZ}}

You can change the definition of the macro as you like because the content is ignored by ProZ. Then you must introduce a generic definition of \prozignore. The definition is ignored by ProB, but Fuzz needs it for type checking.

%%pregen \prozignore
\begin{gendef}[X]
  \prozignore~\_ : \power X
\end{gendef}

It is also possible to append these lines to the "fuzzlib" in the fuzz distribution.

Translation to B

You can inspect the result of the translation process with "Show internal representation" in the "Debug" menu. Please note that the shown B machine is normally not syntactically correct because of

additional constructs like free types
additional type information of the form "var:type"
names with primes (') or question marks, etc.
lack of support from the pretty printer for every construct

Known Limitations

Generic definitions are not supported yet.
Miscellaneous unsupported constructs
- reflexive-transitive closure
- probably other?
The error messages are not very helpful yet.

Summary of Supported Operators

Logical predicates:
-------------------
 P \land Q         conjunction
 P \lor Q          disjunction
 P \implies Q      implication
 P \iff Q          equivalence
 \lnot P           negation
 
Quantifiers:
------------
 \forall x:T | P @ Q      universal quantification (P => Q)
 \exists x:T | P @ Q      existential quantification (P & Q)
 \exists_1 x:T | P @ Q    exactly one existential quantification

Sets:
----- 
  \emptyset        empty set
  \{E,F\}          set extension
  \{~x:S | P~\}    set comprehension
  E \in S          element of
  E \notin S       not element of
  S \cup T         union
  S \cap T         intersection
  S \setminus T    set difference
  \power S         power set
  \# S             cardinality
  S \subseteq T    subset predicate
  S \subset T      strict subset
  \bigcup A        generalized union of sets of sets
  \bigcap A        generalized intersection of sets of sets

Pairs:
------
  E \mapsto F      pair
  S \cross T       Cartesian product
  first E          first part of pair
  second E         second part of pair

Numbers:
--------
  \nat             Natural numbers
  \num             Integers
  \nat_1           Positive natural numbers
  m < n            less
  m \leq n         less equal
  m > n            greater
  m \geq n         greater equal
  m + n            addition
  m - n            difference
  m * n            multiplication
  m \div n         division
  m \mod n         modulo**
  m \upto n        m..n
  min S            minimum of a set
  max S            maximum of a set
  succ n           successor of a number

**:  modulo of negative numbers not supported

Functions:
----------
  S \rel T         relations
  S \pfun T        partial functions from S to T
  S \fun T         total functions from S to T
  S \pinj T        partial injections from S to T
  S \inj T         total injections from S to T
  S \bij T         total bijections from S to T
  \dom R           domain
  \ran R           range
  \id S            identity relation over S
  S \dres R        domain restriction
  S \ndres R       domain anti-restriction
  R \rres S        range restriction
  R \nrres S       range anti-restriction
  R \oplus Q       overriding
  R \plus          transitive closure

Sequences:
----------
  \langle E,... \rangle   explicit sequence
  \seq S           sequences over S
  \seq_1 S         non-empty sequences
  \iseq S          injective sequences over S
  rev E            reverse a sequence
  head E           first element of a sequence
  last E           last element of a sequence
  tail E           sequence with first element removed
  front E          all but the last element
  E \cat F         concatenation of two sequences
  \dcat ss         concatenation of sequences of sequences
  E \filter F      subsequence of elements of sequence E contained in set F
  E \extract F     extract subsequence from F with indexes in set E
  squash F         compaction
  E \prefix F      sequence E is a prefix of F
  E \suffix F      sequence E is a suffix of F
  E \inseq F       E is a sequence occuring in the middle of F (segment relation)
  \disjoint E      family of sets E is disjoint
  E \partition F   family of sets E is a partition of set F

Bags:
----------
  \bag S              bags over S
  \lbag E,... \rbag   explicit bag
  count B E           count of occurences of E in bag B
  B \bcount E         infix version of count
  E \inbag B          bag membership
  B \subbageq C       sub-bag relation
  B \uplus C          bag union
  B \uminus C         bag difference
  items E             bag of items in a sequence
  n \otimes B         bag scaling

Other:
-----------
\IF P \THEN E \ELSE F   if-then-else expression
(\LET x == E @ F)       Let-expression

[1] M. Butler and M. Leuschel: Combining CSP and B for specification and property verification. FM 2005, LNCS 3582, Springer-Verlag, 2005 [1]

[2] ProB provides support for LTL and CTL model checking (citations needed).

[1]

[1]

Handbook/Other Languages

Other recognised Prolog predicates

ProB (1) for Rodin

ProB 2.0 for Rodin

Multi-Simulation for Rodin based on ProB

Other Plug-Ins for Rodin

Prover Evaluation

Camille

Installation

Animation and Modelchecking

Export for use with the Tcl/Tk version of ProB

Theories

Tagging operators

Download Theories

Download Theories

Tagging operators

Error Messages

Examples

Limitations of CSP-M Support

Guiding B Machines with CSP

Command Line option for guided CSP||B

References

Details of supported CSP-M syntax

PROCESS DEFINITIONS

PROCESS EXPRESSIONS

BOOLEAN EXPRESSIONS

VALUE EXPRESSIONS

COMMENTS

PRAGMAS

Supported CSP Assertions in ProB

CSP Assertions Viewer

Debugging Non-satisfied Assertions

Checking CSP Assertions with `probcli`

References and Notes

Installation

Examples

N-Queens

River Crossing Puzzle

Proof with Atelier-B Example

Alloy Syntax

Using ProB for Animation and Model Checking of TLA+ specifications

TLA2B

Supported TLA+ syntax

Limitations of the translation

TLA+ Actions

Understanding the type checker

Preferences

Structure of the Z Specification

State and Initialization

Operations

Axiomatic definitions

Invariant

Scope

Abbreviation Definitions

Graphical animation

Special constructs

prozignore

Translation to B

Known Limitations

Summary of Supported Operators