Rush Hour XTL
This case studies tackles encoding the rush hour board game in which cars are packed on a 6-by-6 grid and can either move horizontally or vertically. The goal is to move the red car to the exit. In this particular instance we try to solve the hardest puzzle of the original game Nr. 40.
This is a Prolog XTL encoding of the B solution which is also available. On the Prolog XTL encoding presented here ProB finds the example in one second (on a Mac Book Air, 1.7 GHz i7), on the B version it takes ProB about 10 seconds (but the TLC backend is faster). Part of the B models are shown in comments for reference below. This file needs to be saved with a .P extension so that it can be loaded by ProB Tcl/Tk or probcli.
Observe how we use sort and ord_add_element to avoid multiple versions of the same state. The important predicates that ProB uses are start/1, trans/3 and prop/2.
/* a Prolog XTL translation of the more elegant encoding of the Rush Hour puzzle */
/* Michael Leuschel, July 2014 */
/* ProB finds solution in about 0.5 - 1 second *using mixed DF/BF search */
/* Using BF search it takes 1.3 seconds */
/* This shows the potential of compiling the ProB B interpreter down to Prolog */
/* The Prolog could still be optimized further (e.g. run through a partial evaluator ) */
%:- use_module(library(lists)). % not needed when run from ProB
%:- use_module(library(ordsets)). % not needed when run from ProB
sze([2,2,2,2,2, 2,2,2,2, 3,3,3, 2]). /* the sizes of the cars */
dir([v,v,v,v,v, h,h,h,h, v,v,h, h]). /* indicating whether the cars move vertically or horizontally */
red(Len) :- sze(S), length(S,Len). /* the last car is the red one */
dim(5). /* the grid goes from 0..dim */
free_initial([(0,3),(1,3), (0,5), (3,4),(4,0),(4,1),(5,5)]).
col_initial([(1),(2),(2),(3),(4), /* vertical 2-size cars */
(0),(1),(3),(4), /* horiz. 2-size cars */
(0),(5), /* vertical 3-size cars */
(0), /* horiz. 3-size cars */
(3)] /* red car */
).
row_initial([(1),(1),(4),(3),(0),
(5),(0),(5),(4),
(0),(1),
(3),
(2)]).
init(S) :- start(S).
start(rcf(Rows,Cols,SFree)) :- free_initial(Free),
sort(Free,SFree),
row_initial(Rows),
col_initial(Cols).
prop(rcf(_,_,Free),free(I,J)) :- member((I,J),Free).
prop(rcf(Rows,Cols,_),car(Car,Row,Col)) :- nth1(Car,Rows,Row),nth1(Car,Cols,Col).
/*
prop(rcf(_,_,Free),unsafe) :- member((N,M),Free), (N>5 ; N<0 ; M>5 ; M<0).
prop(rcf(Rows,_,_),unsafe) :- member(N,Rows), (N>5 ; N<0).
prop(rcf(_,Cols,_),unsafe) :- member(N,Cols), (N>5 ; N<0).
*/
prop(rcf(_Rows,Cols,_Free),unsafe) :- last(Cols,4). /* The target : move red car to the right */
% utility for updating lists of columns/rows:
replace([_|T],1,New,Res) :- !, Res=[New|T].
replace([H|T],N,New,[H|TR]) :- N1 is N-1, replace(T,N1,New,TR).
trans(mv_down(Car,F),rcf(Rows,Cols,Free),rcf(Rows1,Cols,SFree1)) :-
dir(Dir),
nth1(Car,Dir,v),
nth1(Car,Rows,RC),
nth1(Car,Cols,CC),
sze(Sze),
nth1(Car,Sze,SC),
FR is RC+SC, F = (FR,CC),
select(F,Free,Free0),
ord_add_element(Free0,(RC,CC),SFree1),
RC1 is RC+1,
replace(Rows,Car,RC1,Rows1).
/*
mv_down(c,F) = PRE c:1..red & c |-> v : dir & F = row(c)+sze(c)|->col(c) &
F : free THEN
free := free - {F} \/ {row(c)|->col(c)} ||
row(c) := row(c)+1
END;
*/
trans(mv_up(Car,F),rcf(Rows,Cols,Free),rcf(Rows1,Cols,SFree1)) :-
dir(Dir),
nth1(Car,Dir,v),
nth1(Car,Rows,RC),
nth1(Car,Cols,CC),
FR is RC-1, F = (FR,CC),
select(F,Free,Free0),
sze(Sze),
nth1(Car,Sze,SC),
RSC1 is RC+SC-1,
ord_add_element(Free0,(RSC1,CC),SFree1),
replace(Rows,Car,FR,Rows1).
/*
mv_up(c,F) = PRE c:1..red & c |-> v : dir & F = row(c)-1|->col(c) &
F : free THEN
free := free - {F} \/ {row(c)+sze(c)-1|->col(c)} ||
row(c) := row(c)-1
END; */
trans(mv_right(Car,F),rcf(Rows,Cols,Free),rcf(Rows,Cols1,SFree1)) :-
dir(Dir),
nth1(Car,Dir,h),
nth1(Car,Rows,RC),
nth1(Car,Cols,CC),
sze(Sze),
nth1(Car,Sze,SC),
CCS is CC+SC, F = (RC,CCS),
select(F,Free,Free0),
ord_add_element(Free0,(RC,CC),SFree1),
CC1 is CC+1,
replace(Cols,Car,CC1,Cols1).
/*
mv_right(c,F) = PRE c:1..red & c |-> h : dir & F = row(c)|->col(c)+sze(c) &
F : free THEN
free := free - {F} \/ {row(c)|->col(c)} ||
col(c) := col(c)+1
END; */
trans(mv_left(Car,F,RC,CC,SC,CCS),rcf(Rows,Cols,Free),rcf(Rows,Cols1,SFree1)) :-
dir(Dir),
nth1(Car,Dir,h),
nth1(Car,Rows,RC),
nth1(Car,Cols,CC),
CC1 is CC-1, F = (RC,CC1),
select(F,Free,Free0),
sze(Sze),
nth1(Car,Sze,SC),
CCS is CC1+SC,
ord_add_element(Free0,(RC,CCS),SFree1),
replace(Cols,Car,CC1,Cols1).
/*
mv_left(c,F) = PRE c:1..red & c |-> h : dir & F = row(c)|->col(c)-1 &
F : free THEN
free := free - {F} \/ {row(c)|->col(c)+sze(c)-1} ||
col(c) := col(c)-1
END
END
*/
We can also add a simple graphical visualisation by including the following in the XTL file (using the animation_function_result predicate recognised by ProB as of version 1.4.0-rc3):
% Graphical Visualization Animation Function:
is_index(I,I).
is_index(I,Res) :- dim(N), I<N, I1 is I+1, is_index(I1,Res).
animation_function_result(State,Matrix) :-
findall(((RowNr,ColNr),Cell), (is_index(0,RowNr),is_index(0,ColNr),
cell_content(State,RowNr,ColNr,Cell)),Matrix).
cell_content(rcf(Rows,Cols,Free),Row,Col,'--') :- member((Row,Col),Free).
cell_content(rcf(Rows,Cols,Free),Row,Col,Car) :- nth1(Car,Rows,Row), nth1(Car,Cols,Col).
cell_content(rcf(Rows,Cols,Free),Row1,Col,Car) :- dir(Dir),
sze(Sze),
nth1(Car,Dir,v),
nth1(Car,Sze,SC),
nth1(Car,Rows,Row), nth1(Car,Cols,Col),
(Row1 is Row+1 ; SC>2, Row1 is Row+2).
cell_content(rcf(Rows,Cols,Free),Row,Col1,Car) :- dir(Dir),
sze(Sze),
nth1(Car,Dir,h),
nth1(Car,Sze,SC),
nth1(Car,Rows,Row), nth1(Car,Cols,Col),
(Col1 is Col+1 ; SC>2, Col1 is Col+2).
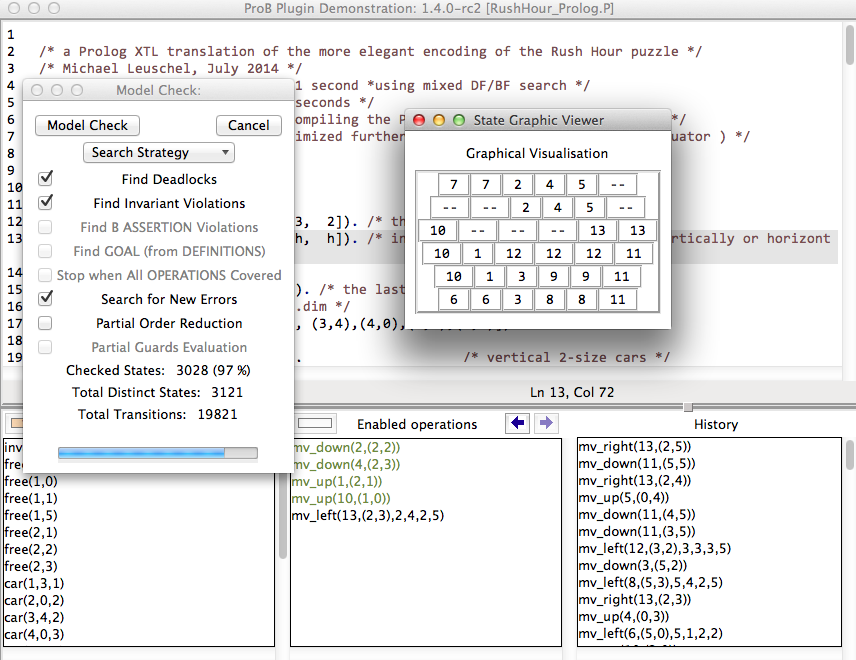
Here is a screenshot of ProB after finding the shortest solution using model checking.
You can see the (simple) graphical visualisation of the state of the model.
Running using probcli
Here is how you can find the solution using probcli (run on a Mac Book Air, 1.7 GHz i7):
$ probcli -mc 100000 RushHour_Prolog.P -bf tcltk_open_xtl_file(/Users/leuschel/git_root/prob_examples/public_examples/B/Puzzles/RushHour/RushHour_Prolog.P) new_xtl_file(/Users/leuschel/git_root/prob_examples/public_examples/B/Puzzles/RushHour/RushHour_Prolog.P) found_error(xtl_error,3026) finding_trace_from_to(root) .................... Model Checking Time: 1310 ms States analysed: 3026 Transitions fired: 19821 *** COUNTER EXAMPLE FOUND *** xtl_error *** TRACE: 1: start_xtl_system: 2: mv_right(8,(5,5)): 3: mv_down(4,(5,3)): 4: mv_up(11,(0,5)): 5: mv_right(12,(3,3)): 6: mv_down(10,(3,0)): 7: mv_left(7,(0,0),0,1,2,2): 8: mv_right(12,(3,4)): 9: mv_up(2,(0,2)): 10: mv_down(1,(3,1)): 11: mv_down(10,(4,0)): 12: mv_right(12,(3,5)): 13: mv_left(13,(2,2),2,3,2,4): 14: mv_down(1,(4,1)): 15: mv_up(3,(3,2)): 16: mv_right(6,(5,2)): 17: mv_left(13,(2,1),2,2,2,3): 18: mv_down(10,(5,0)): 19: mv_left(13,(2,0),2,1,2,2): 20: mv_down(2,(2,2)): 21: mv_right(7,(0,2)): 22: mv_down(5,(2,4)): 23: mv_right(7,(0,3)): 24: mv_right(7,(0,4)): 25: mv_up(2,(0,2)): 26: mv_right(13,(2,2)): 27: mv_up(10,(2,0)): 28: mv_left(6,(5,0),5,1,2,2): 29: mv_down(3,(5,2)): 30: mv_left(12,(3,2),3,3,3,5): 31: mv_right(13,(2,3)): 32: mv_up(1,(2,1)): 33: mv_up(1,(1,1)): 34: mv_left(12,(3,1),3,2,3,4): 35: mv_up(10,(1,0)): 36: mv_up(10,(0,0)): 37: mv_up(1,(0,1)): 38: mv_left(12,(3,0),3,1,3,3): 39: mv_up(4,(3,3)): 40: mv_left(13,(2,1),2,2,2,3): 41: mv_up(4,(2,3)): 42: mv_up(4,(1,3)): 43: mv_right(12,(3,3)): 44: mv_down(10,(3,0)): 45: mv_down(11,(3,5)): 46: mv_right(7,(0,5)): 47: mv_up(4,(0,3)): 48: mv_right(13,(2,3)): 49: mv_right(12,(3,4)): 50: mv_down(1,(2,1)): 51: mv_down(1,(3,1)): 52: mv_down(1,(4,1)): 53: mv_left(13,(2,1),2,2,2,3): 54: mv_down(4,(2,3)): 55: mv_left(7,(0,3),0,4,2,5): 56: mv_up(11,(0,5)): 57: mv_right(12,(3,5)): 58: mv_up(3,(3,2)): 59: mv_right(6,(5,2)): 60: mv_down(10,(4,0)): 61: mv_down(10,(5,0)): 62: mv_left(13,(2,0),2,1,2,2): 63: mv_down(2,(2,2)): 64: mv_left(7,(0,2),0,3,2,4): 65: mv_left(7,(0,1),0,2,2,3): 66: mv_left(7,(0,0),0,1,2,2): 67: mv_up(2,(0,2)): 68: mv_right(13,(2,2)): 69: mv_left(9,(4,3),4,4,2,5): 70: mv_up(10,(2,0)): 71: mv_left(6,(5,0),5,1,2,2): 72: mv_up(4,(0,3)): 73: mv_right(13,(2,3)): 74: mv_left(8,(5,3),5,4,2,5): 75: mv_down(3,(5,2)): 76: mv_left(12,(3,2),3,3,3,5): 77: mv_down(11,(3,5)): 78: mv_down(11,(4,5)): 79: mv_up(5,(0,4)): 80: mv_right(13,(2,4)): 81: mv_down(11,(5,5)): 82: mv_right(13,(2,5)): ! *** error occurred *** ! xtl_error
The full states has 4781 states (including the root node) and 29889 transitions. This is the output of ProB's coverage statistics:
STATES deadlocked:0 open:0 live:4781 total:4781 TOTAL_OPERATIONS 29889 COVERED_OPERATIONS mv_down:8461 mv_left:6483 mv_right:6483 mv_up:8461 start_xtl_system:1 UNCOVERED_OPERATIONS
Complete model checking, without looking for goal states, takes 1.6 seconds (on a Mac Book Air, 1.7 GHz i7):
$ probcli -mc 100000 RushHour_Prolog.P -noinv --coverage tcltk_open_xtl_file(/Users/leuschel/git_root/prob_examples/public_examples/B/Puzzles/RushHour/RushHour_Prolog.P) new_xtl_file(/Users/leuschel/git_root/prob_examples/public_examples/B/Puzzles/RushHour/RushHour_Prolog.P) % All open nodes visited Model Checking Time: 1610 ms States analysed: 4780 Transitions fired: 29889 No Counter Example found. ALL nodes visited. Coverage: [STATES,deadlocked:0,open:0,live:4781,total:4781,TOTAL_OPERATIONS,29889,COVERED_OPERATIONS,mv_down:8461,mv_left:6483,mv_right:6483,mv_up:8461,start_xtl_system:1,UNCOVERED_OPERATIONS]