Tutorial Enabling Analysis
The B-method and in particular its successor Event-B are methodologies for formal development and verification of systems. In Event-B, a machine is usually viewed as a reactive system executing continuously enabled (atomic) events in an interleaved fashion. Thus, parallel events of the system are easily modeled as an interleaving of operation executions. On the other hand, the introduction of abstract counters is required when events are supposed to be executed in some (sequential) order. This, however, can in some cases slow the work of understanding and verifying a model since identifying the sequential ordering of events in an Event-B model is not that obvious. Thus, using methods for determining the control flow can be sometimes very beneficial for understanding the model, as well as for techniques for automatic verification such as model checking.
In this tutorial we present a static analysis for B and Event-B that can be used to reveal the control flow of a machine and to optimize model checking of models written in B and Event-B (see also Tutorial on Partial Guard Evaluation ). The results of the analysis, designated also as ‘’enabling analysis’’, can be presented as relations by means of a table or by means of a graph. For simplicity, we will concentrate mainly on B and use the terminology of the formalism.
Enabling Relations
What we want to find out is how the operations influence each other within a B model. In other words, for each pair (op1,op2) of operations we try to determine as precise as possible how op1 can affect the guard condition of op2 with regard to enabledness. To determine the enabling relations between operations we use syntactic analyses, as well as the constraint-based abilities of ProB.
Consider the following B machine:
MACHINE Example
VARIABLES x, y, z
INVARIANT
x:NATURAL
& y:INTEGER
& z:INTEGER
INITIALISATION
x:=6 || y:=-2 || z:=0
OPERATIONS
Op1 = PRE x + y>=4 THEN x:=x+2 || y:=2 END;
Op2 = PRE x mod 2=1 THEN x:=x+1 || y:=2 END;
Op3 = PRE x mod 2=0 THEN x:=x+2 END;
Op4 = PRE x<0 THEN y:=y-1 END;
Op5 = PRE y/=2 THEN z:=3 END
END
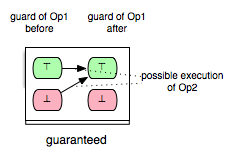
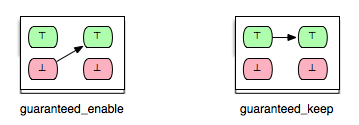
The machine has three variables x,y,z, where x ranges over the domain of natural numbers and y and z over the domain of all integers. For this machine we have 25 pairs of operations for which we want to determine the respective enabling relations. Additionally, we identify 5 further pairs that show the influence of the INITIALISATION on the guard conditions of all other operations. Consider, for example, the pair (Op2,Op1) in Example.mch. Clearly, Op1 is enabled in each state of Example.mch where the predicate ‘x+y>=4’ is fulfilled. Since the effect of Op2 assigns 2 to y and increments x by one upon condition that x is a positive odd number in the before-state of Op2, we can assume that Op1 is always enabled after the execution of Op2. In other words, in all after-states of Op2 the operation Op1 is guaranteed to be enabled. This relation between Op2 and Op1 we can illustrate as follows:
In the figure above the green boxes denote that the evaluation of the guard of Op1 is true, whereas the red boxes denote that the evaluation of the guard of Op1 is false.
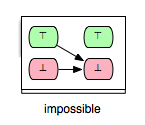
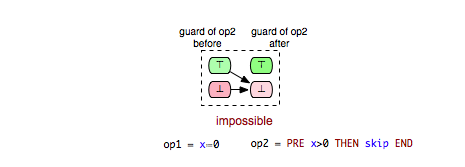
Another pair of interest is (Op2,Op5) in Example.mch. Clearly, Op5 is enabled only in those states in which y is not equal to 2. Obviously, in each after-state of Op2 y is equal to 2 and thus we can conclude that Op5 is impossible to be enabled after each execution of Op2. Such a relation between two operations we denote as ‘’impossible’’ and can be illustrated as follows:
Both arrows in the illustration of the ‘’impossible’’ relation indicate that whether the guard condition of Op5 is fulfilled or not in a before-state of Op2 operation Op5 will be disabled in the respective after-state of Op2. In order to recognize a tuple (op1,op2) as ‘’impossible’’ we require that op2 is always disabled after op1 without further considering whether op2 is always enabled or always disabled in the before-states of op1.
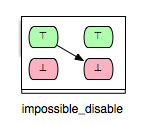
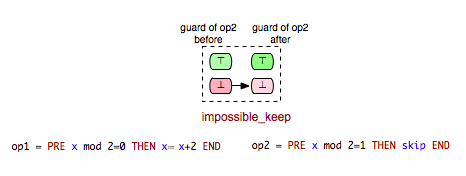
Consider, for instance, the pair (Op2, Op2) in the machine above. We can easily conclude that Op2 becomes disabled after it is executed and clearly, the second case (\false -> \false) of the impossible relation is not possible for (Op2, Op2). This gives rise of introducing another (more precise) impossible relation:
Accordingly, we can derive another relation from ‘’impossible’’ for which only the second case of the ‘’impossible’’ relation is fulfilled:
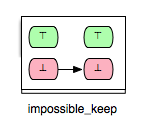
As an example for a pair of operations that fulfills the ‘’impossible_keep’’ requirement you can take, for example, the pair (Op3,Op2) from Example.mch. Since Op2 and Op3 cannot be both enabled in a state and the execution of Op3 cannot enable Op2, then we can easily conclude that Op2 remains always disabled after Op3.
Similarly as for ‘’impossible’’, one could derive two further enabling relations from ‘’guaranteed’’:
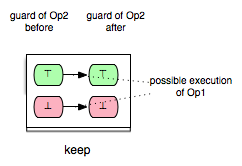
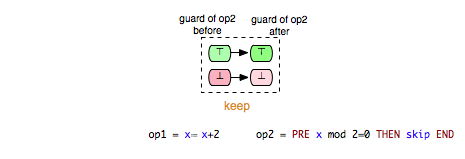
Another interesting class of enabling relations that could be helpful for better understanding and analyzing B and Event-B models is that of the ‘’keep’’ relations. We say that an operation op1 ‘’keeps’’ another operation op2 if op1 cannot change the status of the enabling condition of op2, i.e. op1 keeps op2 enabled respectively disabled. This relationship could be illustrated as follows:
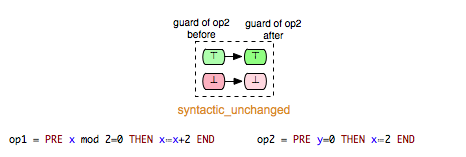
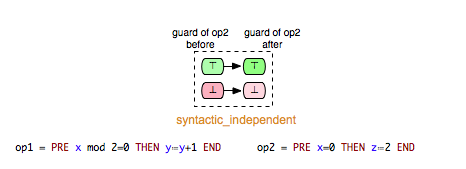
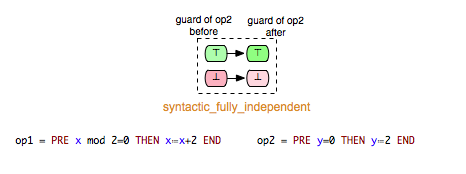
We can take (Op1,Op2) and (Op1,Op3) as examples of pairs in Example.mch that are elements of the keep relation. ‘’keep’’ relations can sometimes be easily determined by analyzing just the syntactic structure of both operations, or more precisely the “read” and “write” sets of both operations.[1] If, for example, an operation op1 does not write any variable of the machine that is read in the guard condition of op2, then we can infer that op1 ‘’keeps’’ op2. In that case we also say that op1 does not change op2 syntactically. In the class of the ‘’keep’’ relations are included also relations such as independence. Two operations op1 and op2 are called independent if each of them cannot disable the other operation and the both orders of execution <op1,op2> and <op2,op1> have the same effect.[2]
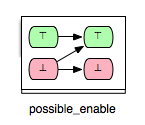
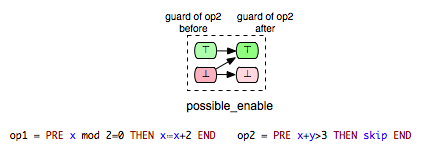
All three classes (‘’guaranteed’’, ‘’impossible’’ and ‘’keep’’) of enabling relations presented so far represent definite relations. That is, if a pair of operations (op1,op2) is confirmed to be a relation of one of this three classes, then we can certainly say what effect on the enabling condition of op2 would the execution of op1 have. However, for some pairs of operations we cannot certainly say what effect an operation would have on the enabling condition of another operation. This is due to the fact that the enabling status of an operation does not only depend on the effect of the executed operations, but also on the current variables’ evaluation. Take, for instance, the tuple (Op3,Op1) from the B machine above. Considering the action part of Op3 and the guard condition of Op1 we can assume that Op3 can enable Op1. Since the guard of Op1 depends not only on the current value of x, but also on y, there could be transitions s -> s' of Op3 in the state space of the machine where Op1 is disabled in both states s and s’. Though, what we could definitely say is that Op3 cannot disable Op1. This relationship we can illustrate as follows:
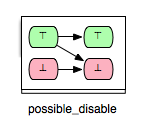
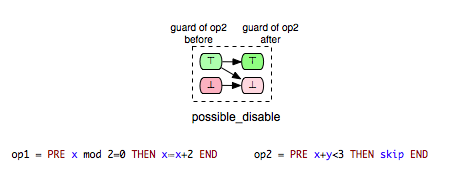
The opposite relation of “possible_enable” is the relation where an operation op2 can disable another operation op1. Formally, we say that op2 can disable op1 if op2 may disable op1 and op2 cannot enable op1. This relationship is denoted as “possible_disable” and can be illustrated as follows:
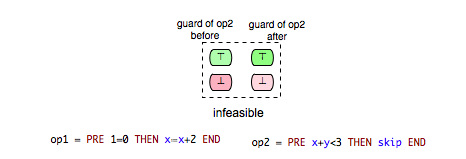
In order to determine how operations influence each other we need to assure first that these are feasible. An operation ‘’op’’ is said to be feasible if there is a state of the machine that satisfies the invariant of the machine and in which ‘’op’’ is enabled. In the B machine above the operation Op4, for example, is not feasible. Obviously, Op4 is enabled only in states where x is a negative number and states in which x is a negative number are visibly not consistent with the invariant since "x : NATURAL". Such incompatibilities are sometimes of great importance for the modeler and therefore they should be revealed in the process of computing the enabling relations. In our case for each pair of operations (Op4,-) and (-,Op4) the status “infeasible” will be returned.
We can now list all possible enabling relations for the machine Example.mch by means of a table. For each entry in the table the operation in the row is the operation whose effect is studied on the status of the guard of the operation in the column.
Summary of the Enabling Relations
In the following, we summarize most of the enabling relations that we think can provide a useful feedback to the user. For each of the enabling relations we have given an appropriate example. In the examples below we compute the effect of executing ‘op1’ on the status of the guard of ‘op2’. The relation identifiers are the same as they appear as results in ProB.
- guaranteed: op2 guaranteed to be executable after op1.
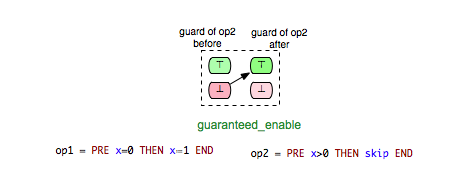
- guaranteed_enable: op2 is guaranteed to become enabled after op1.
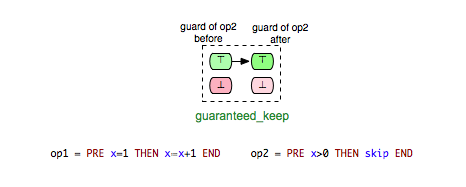
- guaranteed_keep: op2 is guaranteed to stay enabled after op1.
- impossible: op2 is impossible to be executed after op1.
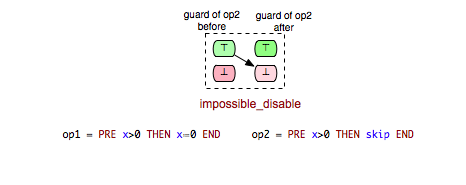
- impossible_disable: op2 is guaranteed to become disabled after op1.
- impossible_keep: op2 is impossible to become enabled after op1.
- keep: op2 always stays enabled resp. disabled after op1.
- syntactic_unchanged: op1 does not write any variable read in the guard of op2, i.e. write(op1) /\ read(op2) = {}
- syntactic_independent: op1 and op2 are syntactically independent, i.e. read(op1) /\ write(op2) = {} & write(op1) /\ read(op2) = {} & write(op1) /\ write(op2) = {}
- syntactically_fully_independent: op1 and op2 are syntactically independent and additionally, read(op1) /\ read(op2) = {}
- possible_enable: op2 possible after op1, but op2 cannot be disabled by op1.
- possible_disable: op2 possible after iop1, but op2 cannot be enabled by op1.
- infeasible: op1 is not feasible and thus cannot influence op2.
Performing Enabling Analysis within ProB
The enabling analysis has been implemented in the ProB toolset. The computation of the enabling relations is based on syntactic and constraint-based techniques. The identification of relations such as ‘’syntactic_independent’’ and ‘’syntactic_unchanged’’ requires just a thorough study of the syntactic structure of the operations, i.e. no calls to the constraint solver have to be made. However, to confirm, for example, that an operation is guaranteed or impossible to be executed after another operation the use of the ProB’s constraint solver is unavoidable. For instance, consider the pair (Op2,Op1) from Example.mch. As we have seen, in Example.mch the operation Op1 is guaranteed to be enabled after each execution of Op2. In ProB this could be computed by feeding the (before-after) predicate “ (x mod 2 = 1) => [x:=x+1 || y:=2] (x+y<4)” into the constraint solver. As a result, the constraint solver will not find a solution for the predicate, i.e. the constraint solver will not find a state ‘’s’’ satisfying “x mod 2 = 1” from which after executing Op2 at ‘’s’’ a solution state s’ will be found that fulfills “x+y<4”; note that “x+y<4” is the negation of the guard of Op1. Since there is no after-state of Op2 at which Op1 is disabled we can conclude that Op1 is guaranteed to be executed after Op2. When constraints are getting more complex the constraint solver may need more time for solving and determining the enabling relations may become a very time-expensive task. Therefore, a time-out for each constraint solver call is set. In other words, if the constraint solver does not find a solution in the given time by the user, then the respective relation will be denoted as time-outed. By default, in ProB the time-out for each constraint solver call is set to 300 ms.
Within ProB Tcl/Tk you can find the menu "Enabling Analysis" in the "Analysis" menu of the menu bar.
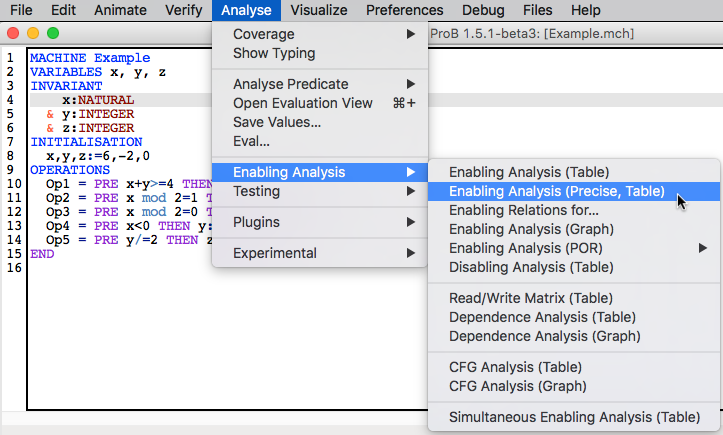
The "Enabling Analysis" menu provides multiple commands:
- "Enabling Analysis (Table)": this command performs a (fast) enabling analysis on the respective B model using a time-out of 300 ms for the constraint-solver calls. The result of the enabling analysis is shown in a table. The table lists all enabling relations between the operations of the loaded B model. These can be exported to a CSV file. The table for Example.mch at the end of the Enabling Relations section was constructed this way.
- "Enabling Analysis (Precise, Table)": this command performs an enabling analysis using a time-out of 2800 ms for each of the constraint-solver calls. As for the command above, the result of the analysis is shown in a table that can be exported to a CSV file.
- "Enabling Relations After...": this command computes all the enabling relations involving an operation chosen by the user.
- "Enabling Analysis (Graph)": this command performs the fast enabling analysis but displays the results as a graph. In case the preference "DOT_SHOW_OP_READ_WRITES" is set for each operation the read/write information is displayed.
- "Enabling Analysis (POR)...": this menu provides further commands for another form of enabling analysis the results of which are used for the partial guard evaluation optimisation in ProB.
- "Read/Write Matrix (Table)": this command performs syntactic analysis on the model. The analysis determines the read and write sets for each operation of the machine.
- "Dependence Analysis (Table)": this command performs a dependency analysis for each pair of operations. More specifically, the analysis determines which operations are dependent or independent to each other.
With the command line version of ProB (probcli) one can perform an enabling analysis on a B or Event-B model by means of the -enabling_analysis option. The results of the analysis, as well as intermediate data and some statistics are printed out on the console:
$ probcli Example.mch -enabling_analysis CHECKING ENABLING AFTER INITIALISATION INITIALISATION ---> Op1 :: ok : guaranteed INITIALISATION ---> Op2 :: impossible INITIALISATION ---> Op3 :: ok : guaranteed INITIALISATION ---> Op4 :: impossible INITIALISATION ---> Op5 :: ok : guaranteed ..... CHECKING ENABLING AFTER: Op5 r:[y] / w:[z] Op5 ---> Op1 :: Enable=syntactic_independent Op5 ---> Op2 :: Enable=syntactic_unchanged Op5 ---> Op3 :: Enable=syntactic_fully_independent Op5 ---> Op4 :: Enable=syntactic_unchanged Op5 ---> Op5 :: Enable=syntactic_unchanged % Finished CBC Enabling Analysis 810 ms walltime (770 ms runtime), since start: 1650 ms % CBC Enabling Stats: % Nr of events: 5 % Nr of cbc calls: 30, Timeout results: 2 Origin,Op1,Op2,Op3,Op4,Op5 INITIALISATION,guaranteed,impossible,guaranteed,impossible,guaranteed Op1,timeout_possible_disable,keep,keep,impossible_keep,syntactic_independent Op2,guaranteed,impossible,guaranteed,impossible_keep,impossible Op3,timeout_possible,impossible_keep,guaranteed,impossible_keep,syntactic_fully_independent Op4,impossible_keep,syntactic_unchanged,syntactic_unchanged,syntactic_keep,impossible_keep Op5,syntactic_independent,syntactic_unchanged,syntactic_fully_independent,syntactic_unchanged,syntactic_unchanged
To perform enabling analysis from the command line and save the results to a CSV-file use the following commando:
$ probcli file.mch -enabling_analysis_csv FILE
where FILE is the name of the CSV-file in which the results of the analysis are stored.
References and Footnotes
- ↑ For an operation op the set read(op) denotes the set of variables that are read by op. Accordingly, by write(op) we denote the set of variables that are written by op.
- ↑ See the Tutorial on Partial Order Reduction for more information on independence between operations.