SEND-MORE-MONEY
In this entry we study how to solve the famous verbal arithmetic SEND-MORE-MONEY puzzle. The task is to find the digits S,E,N,D,M,O,R,Y such that the addition of SEND to MORE leads the decimal number MONEY. There are various ways to solve this problem in B using ProB. The quickest is probably to fire up the probcli REPL and then type the problem into the console. To start up the REPL type the following into your shell or terminal:
probcli -repl
This should give you the following output:
ProB Interactive Expression and Predicate Evaluator Type ":help" for more information. >>>
Note, you can also use the Eval Console in ProB Tcl/Tk or the online Logic Calculator. We can now encode the puzzle as a predicate as follows:
>>> {S,E,N,D, M,O,R, Y} <: 0..9 & S>0 & M>0 & card({S,E,N,D, M,O,R, Y})=8 & S*1000 + E*100 + N*10 + D + M*1000 + O*100 + R*10 + E = M*10000 + O*1000 + N*100 + E*10 + Y
After hitting return, ProB will output the following immediately:
Existentially Quantified Predicate over S,E,N,D,M,O,R,Y is TRUE
Solution:
S = 9 &
E = 5 &
N = 6 &
D = 7 &
M = 1 &
O = 0 &
R = 8 &
Y = 2
Let us review the individual conjuncts of the B encoding of the puzzle: The following specifies that S,E,N,D,M,O,R,Y are all digits. Note that <: is the subset operator in B:
{S,E,N,D, M,O,R, Y} <: 0..9
An alternative, slightly longer, encoding would have been to write:
S:0..9 & E:0..9 & N:0..9 & D:0..9 & M:0..9 & O:0..9 & R:0..9 & Y:0..9
The following conjunct specifies that the S and M cannot be 0:
S>0 & M>0
The next conjunct specifies that all digits are distinct:
card({S,E,N,D, M,O,R, Y})=8
Note that an alternative, but much longer encoding would have been to specify inequalities
S /= E & S /= N & S /= D & ... & R/=Y
Finally, the last conjunct expresses the sum constraint:
S*1000 + E*100 + N*10 + D + M*1000 + O*100 + R*10 + E = M*10000 + O*1000 + N*100 + E*10 + Y
We are still not sure if this is the only solution. One way to ensure this is to compute a set comprehension with all solutions:
>>> {S,E,N,D,M,O,R,Y|{S,E,N,D, M,O,R, Y} <: 0..9 & S>0 & M>0 & card({S,E,N,D, M,O,R, Y})=8 & S*1000 + E*100 + N*10 + D + M*1000 + O*100 + R*10 + E = M*10000 + O*1000 + N*100 + E*10 + Y}
Expression Value =
{(((((((9|->5)|->6)|->7)|->1)|->0)|->8)|->2)}
As you can see, only one solution tuple was found.
Instead of solving the puzzle within ProB's console, you can also save the above predicate into a file SendMoreMoney.eval and then issue the command:
probcli -eval_file SendMoreMoney.eval
Existentially Quantified Predicate over S,E,N,D,M,O,R,Y is TRUE
Solution:
S = 9 &
E = 5 &
N = 6 &
D = 7 &
M = 1 &
O = 0 &
R = 8 &
Y = 2
Another alternative is to wrap the predicate into a full B machine, e.g., as PROPERTIES, e.g., into a file SendMoreMoney.mch with the following content:
MACHINE SendMoreMoney
CONSTANTS S,E,N,D, M,O,R, Y
PROPERTIES
{S,E,N,D, M,O,R, Y} <: 0..9 & S >0 & M >0 &
card({S,E,N,D, M,O,R, Y}) = 8 &
S*1000 + E*100 + N*10 + D +
M*1000 + O*100 + R*10 + E =
M*10000 + O*1000 + N*100 + E*10 + Y
END
This machine can then be loaded, e.g., into the ProB Tcl/Tk animator, which should give you a picture like this:
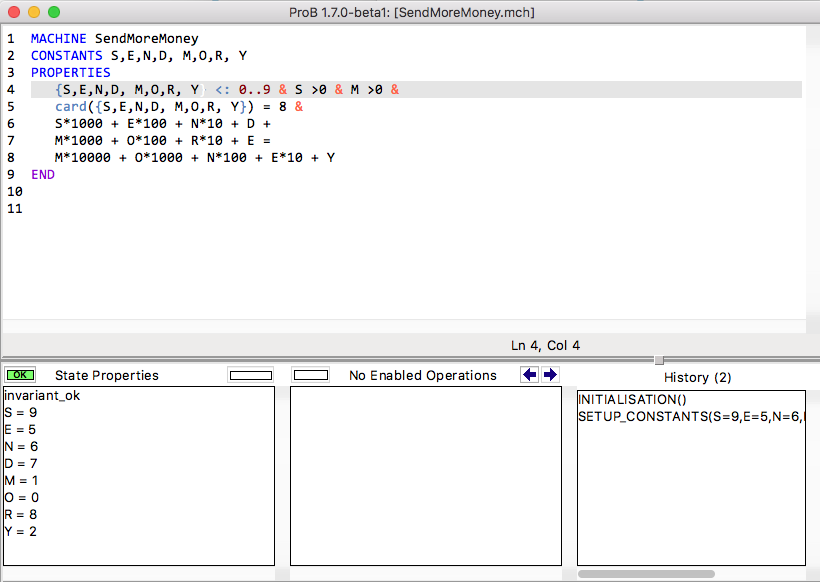
Alternatively you can load the B machine from the command-line using, e.g.:
probcli SendMoreMoney.mch -init -repl
This command will solve the properties and then start the REPL, where you can query the values of the solutions found.
KISS*KISS = PASSION
A similar puzzle, this times involving multiplication is the KISS*KISS=PASSION puzzle. Here we again have distinct digits K, I, S, P, A, O, N such that the square of KISS equals the decimal number passion. The puzzle can be described and solved in a fashion very similar to the problem above:
>>> {K,P} <: 1..9 & {I,S,A,O,N} <: 0..9 & (1000*K+100*I+10*S+S) * (1000*K+100*I+10*S+S) = 1000000*P+100000*A+10000*S+1000*S+100*I+10*O+N & card({K, I, S, P, A, O, N}) = 7
Existentially Quantified Predicate over K,P,I,S,A,O,N is TRUE
Solution:
K = 2 &
P = 4 &
I = 0 &
S = 3 &
A = 1 &
O = 8 &
N = 9