Blocks World (Directed Model Checking): Difference between revisions
No edit summary |
Fix PDF link in reference |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
In this example we want to highlight the new directed model checking features of ProB (available as of version 1.5.1), which allow one to <em>direct</em> the model checker towards a desired goal. Technically speaking, the model checker now maintains a weighted priority queue of unprocessed states, | In this example we want to highlight the new [[Tutorial_Directed_Model_Checking |directed model checking]] features of ProB (available as of version 1.5.1), which allow one to <em>direct</em> the model checker towards a desired goal. Technically speaking, the model checker now maintains a weighted priority queue of unprocessed states, choosing states with minimal weights for processing. The user can influence how the weights for the unprocessed states are to be computed. | ||
The techniques are also explained and evaluated in a scientific paper | The techniques are also explained and evaluated in a scientific paper | ||
<ref name="vispaper">M. Leuschel and J. Bendisposto: Directed Model Checking for B: An Evaluation and New Techniques. In Proceedings SBMF'2010, LNCS 6527. Springer-Verlag, 2010 | <ref name="vispaper">M. Leuschel and J. Bendisposto: Directed Model Checking for B: An Evaluation and New Techniques. In Proceedings SBMF'2010, LNCS 6527. Springer-Verlag, 2010 https://www3.hhu.de/stups/downloads/pdf/LeBe2010.pdf</ref>. | ||
To illustrate the directed model checking feature, we use the following model of Blocks-World, where we manipulate a given set of blocks (a,b,c,d,e,f). A robot arm can pick of blocks (provided no other block is on top of it) and either move it onto a table or onto another block (provided this block has no other block on top of it). | To illustrate the directed model checking feature, we use the following model of Blocks-World, where we manipulate a given set of blocks (a,b,c,d,e,f). A robot arm can pick of blocks (provided no other block is on top of it) and either move it onto a table or onto another block (provided this block has no other block on top of it). | ||
| Line 52: | Line 52: | ||
You can use the <tt>-bf</tt> flag to force breadth-first search, thus obtaining shortest counter-examples (of length 7; model checking time about 3.3 seconds). | You can use the <tt>-bf</tt> flag to force breadth-first search, thus obtaining shortest counter-examples (of length 7; model checking time about 3.3 seconds). | ||
As of version 1.5.1 you can use the <tt>-mc_mode</tt> flag to provide other options to control the model checking. | As of version 1.5.1 you can use the [[Using_the_Command-Line_Version_of_ProB#-mc_mode_.3CM.3E|<tt>-mc_mode</tt>]] flag to provide other options to control the model checking (see also [[Tutorial_Directed_Model_Checking|the tutorial page on directed model checking options]]). | ||
One option is <tt>random</tt>, which gives every node (aka unprocesses state) a random weight. The difference over the mixed depth-first/breadth-first mode is that it completely disregards when nodes where generated. The mixed depth-first/breadth-first mode will try to do a mixture of depth-first and breadth-first traversal; the random mode here is ``just'' random: | One option is <tt>random</tt>, which gives every node (aka unprocesses state) a random weight. The difference over the mixed depth-first/breadth-first mode is that it completely disregards when nodes where generated. The mixed depth-first/breadth-first mode will try to do a mixture of depth-first and breadth-first traversal; the random mode here is ``just'' random: | ||
| Line 104: | Line 104: | ||
[[File:ProB_BlockGoal_Screenshot.png|600px|center]] | [[File:ProB_BlockGoal_Screenshot.png|600px|center]] | ||
When writing your own heuristic functions, keep in mind that internally the weights are stored as 64-bit integers on 64-bit systems, and 32-bit integers on 32-bit systems; currently no overflow checking is performed and larger values for the <tt>HEURISTIC_FUNCTION</tt> expression are silently converted to the respective integer size. | |||
<h3> The complete model for reference </h3> | <h3> The complete model for reference </h3> | ||
Latest revision as of 13:29, 3 February 2021
In this example we want to highlight the new directed model checking features of ProB (available as of version 1.5.1), which allow one to direct the model checker towards a desired goal. Technically speaking, the model checker now maintains a weighted priority queue of unprocessed states, choosing states with minimal weights for processing. The user can influence how the weights for the unprocessed states are to be computed. The techniques are also explained and evaluated in a scientific paper [1].
To illustrate the directed model checking feature, we use the following model of Blocks-World, where we manipulate a given set of blocks (a,b,c,d,e,f). A robot arm can pick of blocks (provided no other block is on top of it) and either move it onto a table or onto another block (provided this block has no other block on top of it). The goal is, given a starting position, to find a plan for the robot to achieve a certain goal (here: block a is on top of b, which is on top of c, ...). We want to use the model checker to find such a plan, i.e., a counter-example found by the model checker is actually a solution to our planning problem.
In B we can model this task as follows. We have two operations, on to move a block onto the table and one to move a block onto another one. The initial configuration is specified in the INITIALISATION; the target is specified by the GOAL definition (which the ProB model checker recognises).
MACHINE BlocksWorldGeneric6
SETS
Objects={a,b,c,d,e,f}
DEFINITIONS
GOAL == (on = ongoal);
ongoal == {a|->b, b|->c, c|->d, d|->e, e|->f}
VARIABLES on
INVARIANT
on: Objects +-> Objects
INITIALISATION
on := {a|->b, c|->a}
OPERATIONS
move_on_table(obj) = PRE obj /: ran(on) & obj : dom(on) THEN
on := {obj} <<| on
END;
move_on_object(obj,onobj) = PRE obj/:ran(on) & onobj /:ran(on) & obj /= onobj THEN
on(obj) := onobj
END
END
Adding a graphical visualization
Adding a graphical visualization is independent of the model checking, but helps visualising the traces found by the model checker. For this we can add ANIMATION_FUNCTION and ANIMATION_FUNCTION_DEFAULT definition, as specified in the complete model at the end of this page.
The initial state of our model then looks as follows, when loaded using ProB Tcl/Tk:
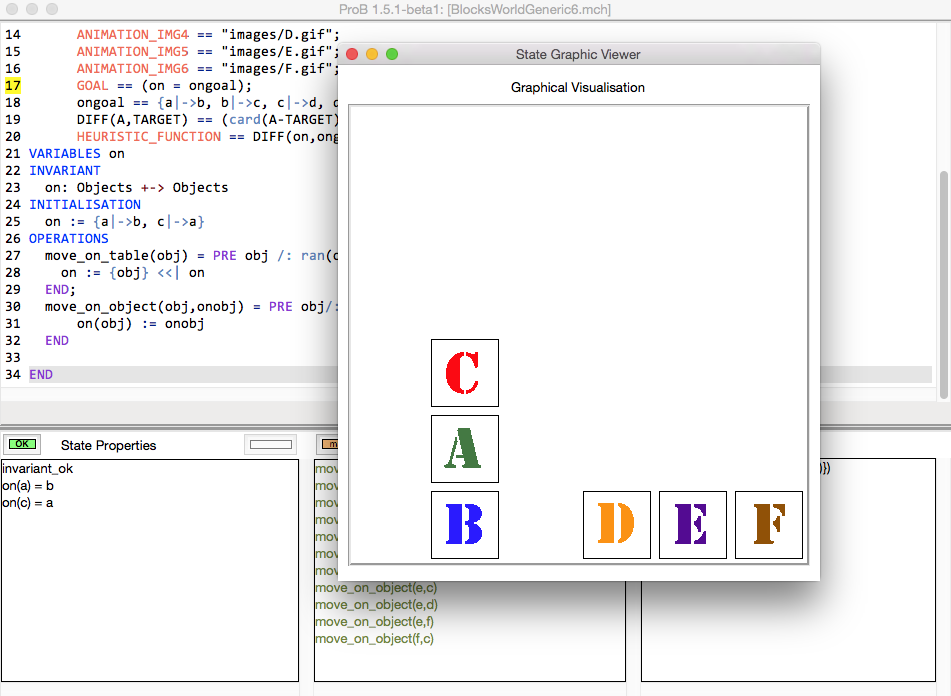
Finding the GOAL
To use the default mixed depth-first/breadth-first search you can type:
$ probcli BlocksWorldGeneric6.mch -model_check
As it has a random component, runtimes vary (typically 0.5 to 3.5 seconds on a Mac Book Air 1.7 GHz). It finds reasonably short counter examples.
You can use depth-first search using the -df flag:
$ probcli BlocksWorldGeneric6.mch -model_check -df
This finds a counter-example of length 48 relatively quickly (120 ms model checking time). You can use the -bf flag to force breadth-first search, thus obtaining shortest counter-examples (of length 7; model checking time about 3.3 seconds).
As of version 1.5.1 you can use the -mc_mode flag to provide other options to control the model checking (see also the tutorial page on directed model checking options).
One option is random, which gives every node (aka unprocesses state) a random weight. The difference over the mixed depth-first/breadth-first mode is that it completely disregards when nodes where generated. The mixed depth-first/breadth-first mode will try to do a mixture of depth-first and breadth-first traversal; the random mode here is ``just random:
probcli BlocksWorldGeneric6.mch -model_check -mc_mode random
A variation of the above is the hash mode, which simply uses the state's Prolog hash as the random weight. The difference is that the result here is predictable, i.e., you will always get the same result when you run the model checker:
probcli BlocksWorldGeneric6.mch -model_check -mc_mode hash
Possibly a more interesting mode is heuristic. It looks for a user-provided DEFINITION for HEURISTIC_FUNCTION and uses this a s priority for states to process next. For example, we can provide the following definition to measure the distance to our target goal:
DIFF(A,TARGET) == (card(A-TARGET) - card(TARGET /\ A));
HEURISTIC_FUNCTION == DIFF(on,ongoal);
Now we get very good model checking time and short counter-examples (aka solution traces):
$ probcli BlocksWorldGeneric6.mch -model_check -mc_mode heuristic
ALL OPERATIONS COVERED
found_error(goal_found,62)
finding_trace_from_to(root)
.
Model Checking Time: 80 ms (80 ms walltime)
States analysed: 12
Transitions fired: 99
*** COUNTER EXAMPLE FOUND ***
goal_found
*** TRACE:
1: INITIALISATION({(a|->b),(c|->a)}):
2: move_on_object(c,d):
3: move_on_object(e,f):
4: move_on_table(c):
5: move_on_object(d,e):
6: move_on_object(c,d):
7: move_on_table(a):
8: move_on_object(b,c):
9: move_on_object(a,b):
! *** error occurred ***
! goal_found
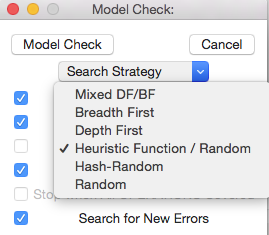
In ProB Tcl/Tk you simply use the standard model checking dialog (in the Verify menu) and choose the "Heuristic Function / Random" option in the "Search Strategy" pop-up menu:
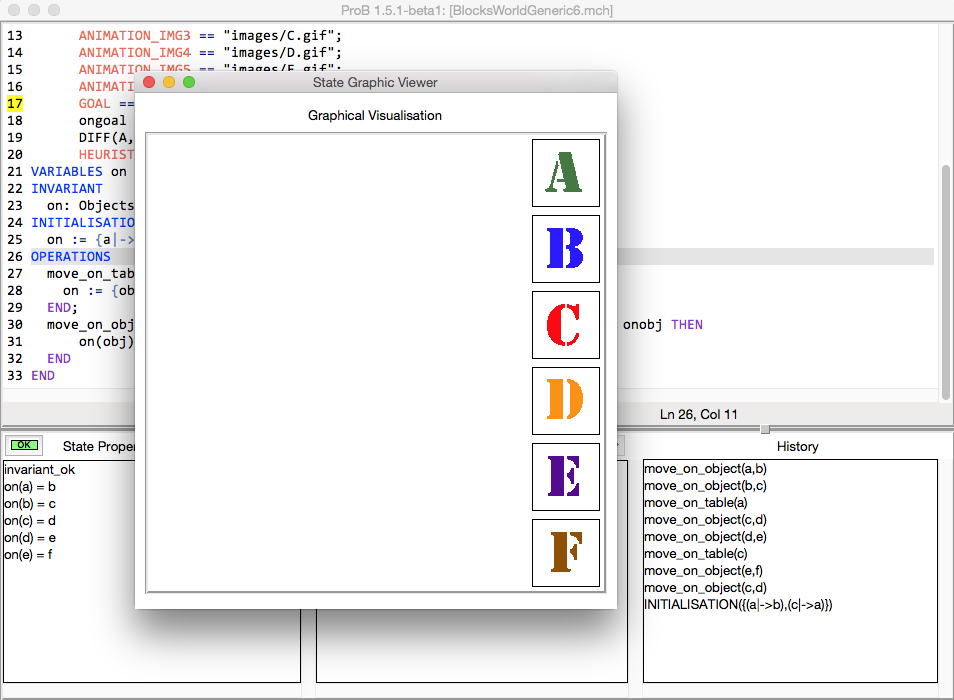
After that you can find the solution quickly by simply pressing the "Model Check" button:
When writing your own heuristic functions, keep in mind that internally the weights are stored as 64-bit integers on 64-bit systems, and 32-bit integers on 32-bit systems; currently no overflow checking is performed and larger values for the HEURISTIC_FUNCTION expression are silently converted to the respective integer size.
The complete model for reference
MACHINE BlocksWorldGeneric6
SETS
Objects={a,b,c,d,e,f}
DEFINITIONS
ANIMATION_FUNCTION_DEFAULT == {r,c,img|r:1..card(Objects) & img=0 & c:1..card(Objects)};
ANIMATION_FUNCTION == ( {r,c,i| r=card(Objects) & i:Objects & c:Objects & c=i & i/:dom(on)} \/
{r,c,i| r:1..(card(Objects)-1) & i:Objects & c:Objects &
i|->c:iterate(on,card(Objects)-r) & c/:dom(on)}
);
ANIMATION_IMG0 == "images/empty_box_white.gif";
ANIMATION_IMG1 == "images/A.gif";
ANIMATION_IMG2 == "images/B.gif";
ANIMATION_IMG3 == "images/C.gif";
ANIMATION_IMG4 == "images/D.gif";
ANIMATION_IMG5 == "images/E.gif";
ANIMATION_IMG6 == "images/F.gif";
GOAL == (on = ongoal);
ongoal == {a|->b, b|->c, c|->d, d|->e, e|->f};
DIFF(A,TARGET) == (card(A-TARGET) - card(TARGET /\ A));
HEURISTIC_FUNCTION == DIFF(on,ongoal);
VARIABLES on
INVARIANT
on: Objects +-> Objects
INITIALISATION
on := {a|->b, c|->a}
OPERATIONS
move_on_table(obj) = PRE obj /: ran(on) & obj : dom(on) THEN
on := {obj} <<| on
END;
move_on_object(obj,onobj) = PRE obj/:ran(on) & onobj /:ran(on) & obj /= onobj THEN
on(obj) := onobj
END
END
References
- ↑ M. Leuschel and J. Bendisposto: Directed Model Checking for B: An Evaluation and New Techniques. In Proceedings SBMF'2010, LNCS 6527. Springer-Verlag, 2010 https://www3.hhu.de/stups/downloads/pdf/LeBe2010.pdf