Help

Rush Hour Puzzle: Difference between revisions
(Update Wikipedia link)
 
(One intermediate revision by one other user not shown)
Line 1: Line 1:
== B Encoding of the Rush Hour Puzzle ==
== B Encoding of the Rush Hour Puzzle ==


This case studies tackles encoding the [http://en.wikipedia.org/wiki/Rush_Hour_(board_game) rush hour board game] in which cars are packed on a 6-by-6 grid and can either move horizontally or vertically. The goal is to move the red car to the exit. In this particular instance we try to solve the [http://www.puzzles.com/products/RushHour/RHfromMarkRiedel/Jam.html?40 hardest puzzle of the original game Nr. 40].
This case studies tackles encoding the [https://en.wikipedia.org/wiki/Rush_Hour_(puzzle) rush hour board game] in which cars are packed on a 6-by-6 grid and can either move horizontally or vertically. The goal is to move the red car to the exit. In this particular instance we try to solve the [http://www.puzzles.com/products/RushHour/RHfromMarkRiedel/Jam.html?40 hardest puzzle of the original game Nr. 40].


Inspired by discussions with Neng-Fa Zhou at ICLP'14 in Vienna, we now have a new version of the B model for this puzzle.
Inspired by discussions with Neng-Fa Zhou at ICLP'14 in Vienna, we now have a new version of the B model for this puzzle.


The old version can still be found below.
The old version can still be found below.
There is also a Prolog [[Other_languages|XTL]] encoding of the [[Rush_Hour_XTL|same problem available]]. Here ProB finds the example in one second or less.
There is also a Prolog [[Other_languages|XTL]] encoding of the [[Rush_Hour_XTL|same problem available]], where ProB finds the example in one second or less.
Explanations and comparison with the [http://picat-lang.org/exs/prob_rushhour.pi Picat solution] will follow soon.
Explanations and comparison with the [http://picat-lang.org/exs/prob_rushhour.pi Picat solution] will follow soon.


Latest revision as of 13:53, 3 February 2021

B Encoding of the Rush Hour Puzzle

This case studies tackles encoding the rush hour board game in which cars are packed on a 6-by-6 grid and can either move horizontally or vertically. The goal is to move the red car to the exit. In this particular instance we try to solve the hardest puzzle of the original game Nr. 40.

Inspired by discussions with Neng-Fa Zhou at ICLP'14 in Vienna, we now have a new version of the B model for this puzzle.

The old version can still be found below. There is also a Prolog XTL encoding of the same problem available, where ProB finds the example in one second or less. Explanations and comparison with the Picat solution will follow soon.

As we show below, the shortest solution can be found very quickly using our new feature to use TLC for model checking B specifications (about 1 second model checking time; rest of time needed to replay counter example).

First, here is the B model of the Rush Hour puzzle: 

MACHINE RushHour
/* a more elegant encoding of the Rush Hour puzzle */
/* Michael Leuschel, July 2014 */
/* ProB finds solution in about 10.5 secs (turning invariant checking off) */
/* This version has been slightly adapted for TLC by adding the c:1..red guards:
    it finds a solution in 3 seconds
   (most of this time is spent replaying the counter ; the model checking seems less than a
    second) */
SETS DIR = {h,v}
CONSTANTS sze, dir, red, dim, free_initial
PROPERTIES
 sze = [2,2,2,2,2,  2,2,2,2,  3,3,3,  2] & /* the sizes of the cars */
 dir = [v,v,v,v,v,  h,h,h,h,  v,v,h,  h] & /* indicating whether the cars move vertically or horizontally */
 red = size(sze) & /* the last car is the red one */
 dim = 5 & /* the grid goes from 0..dim */
 free_initial = {(0,3),(1,3), (0,5), (3,4),(4,0),(4,1),(5,5)}
DEFINITIONS
  GOAL == (col(red) = 4); /* The target : move red car to the right */
  ANIMATION_STR_JUSTIFY_RIGHT == TRUE;
  ANIMATION_FUNCTION_DEFAULT == (0..dim)*(0..dim)*{-1};
  ANIMATION_FUNCTION ==
    {r,c,i| i:1..red & dir(i)=h & row(i)=r & c:col(i)..col(i)+sze(i)-1} \/
    {r,c,i| i:1..red & dir(i)=v & col(i)=c & r:row(i)..row(i)+sze(i)-1}  \/
    free * {0}
VARIABLES free, row, col
INVARIANT
  free <: (0..dim)*(0..dim) &                /* the currently free blocks */
  card(free) = card(free_initial) &
  row : 1..red --> 0..dim &                  /* the row of each car */
  col : 1..red --> 0..dim                    /* the column for each car */
INITIALISATION
 free :=  free_initial
 ||
  col := [(1),(2),(2),(3),(4),                    /* vertical 2-size cars */
          (0),(1),(3),(4),                        /* horiz. 2-size cars */
          (0),(5),                                /* vertical 3-size cars */
          (0),                                    /* horiz. 3-size cars */
          (3)]                                    /* red car */
 ||
  row := [(1),(1),(4),(3),(0),
          (5),(0),(5),(4),
          (0),(1),
          (3),
          (2)]                                    /* red car */
OPERATIONS
  mv_down(c,F) = PRE c:1..red & c |-> v : dir & F = row(c)+sze(c)|->col(c) &
                F : free THEN
            free := free - {F} \/ {row(c)|->col(c)} ||
            row(c) := row(c)+1
    END;
  mv_up(c,F) = PRE c:1..red & c |-> v : dir & F = row(c)-1|->col(c) &
                  F : free THEN
            free := free - {F} \/ {row(c)+sze(c)-1|->col(c)} ||
            row(c) := row(c)-1
    END;
  mv_right(c,F) = PRE c:1..red & c |-> h : dir & F = row(c)|->col(c)+sze(c) &
                F : free THEN
            free := free - {F} \/ {row(c)|->col(c)} ||
            col(c) := col(c)+1
    END;
  mv_left(c,F) = PRE c:1..red & c |-> h : dir & F = row(c)|->col(c)-1 &
                  F : free THEN
            free := free - {F} \/ {row(c)|->col(c)+sze(c)-1} ||
            col(c) := col(c)-1
    END
END

Finding a Solution with ProB

To find a solution you need to run the ProB "Model Check" command in the "Verify" menu. Be sure to enable the "Find GOAL (from DEFINITIONS)" checkbox, as above we have specified the target state col(red) = 4 inside the GOAL definition.

Here is a screenshot of ProB after finding the shortest solution using model checking. As you can see there is also a (simple) graphical visualisation of the state of the model. We have also opened the "Evaluation View".

ProB RushHour v2 Screenshot.png

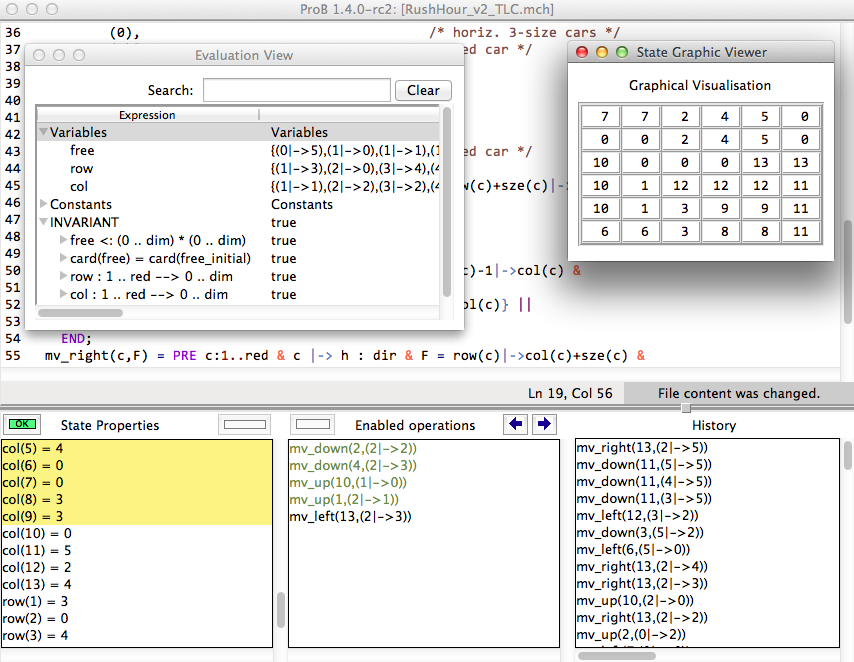
Exporting a Solution Trace

You can inspect or export the solution trace found by ProB in various ways:

  • using the command "History to Current State" in the "Traces" submenu of the "Visualize" menu
  • using various commands in the "Trace Checking" submenu of the "Verify" menu, e.g.:
    • "Save History to Trace File": this generates a Prolog trace file that can be replayed later using the "Check Trace from Trace File" command
    • "Save History to B File...": this saves the trace in B format and it can be parsed by a B parser

Note: you can also find the solution from the command line using probcli: probcli -mc 10000 RushHour.mch. The command line version probcli will output the trace on the console, but also provides various commands to save the history to file.

Finding the shortest solution using the TLC backend

If you want to find the shortest solution with ProB you should set the "Search Strategy" in the ProB "Model Check" command to "Breadth First". The shortest solution has 81 moves (if one allows a car to move multiple spaces in one move then the shortest solution has 51 moves).

You can also use ou It was found in 3 seconds (about 1 second model checking time) using our TLC model checking backend on a Mac Book Air 1.7 GHz i7:

ProB RushHour v2 TLC Dialog.png

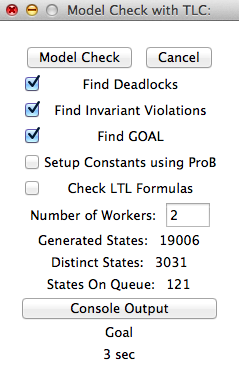
Note; without invariant checking the overall TLC runtime goes down to 2 seconds. Note that we had to add the predicates c:1..red to the guards, as otherwise TLC cannot reduce the domain c to a finite domain. ProB itself has no issue with this, but ProB is slower (about 10 seconds to find a solution trace).

Here is the solution as obtained when saving the trace to a B file (Save History to B File... command in the Verify -> Trace Checking submenu): 

/* Constants
   sze = [2,2,2,2,2,2,2,2,2,3,3,3,2]
 & dir = [v,v,v,v,v,h,h,h,h,v,v,h,h]
 & red = 13
 & dim = 5
 & free_initial = {(0|->3),(0|->5),(1|->3),(3|->4),(4|->0),(4|->1),(5|->5)}
*/
/* Initialisation */
/* Variables
   free = {(0|->3),(0|->5),(1|->3),(3|->4),(4|->0),(4|->1),(5|->5)}
 & col = [1,2,2,3,4,0,1,3,4,0,5,0,3]
 & row = [1,1,4,3,0,5,0,5,4,0,1,3,2]
*/
mv_up(11,(0|->5));
mv_right(8,(5|->5));
mv_down(4,(5|->3));
mv_right(12,(3|->3));
mv_down(10,(3|->0));
mv_down(10,(4|->0));
mv_right(12,(3|->4));
mv_down(1,(3|->1));
mv_down(1,(4|->1));
mv_right(12,(3|->5));
mv_up(3,(3|->2));
mv_right(6,(5|->2));
mv_down(10,(5|->0));
mv_left(7,(0|->0));
mv_up(2,(0|->2));
mv_left(13,(2|->2));
mv_left(13,(2|->1));
mv_left(13,(2|->0));
mv_down(2,(2|->2));
mv_right(7,(0|->2));
mv_right(7,(0|->3));
mv_down(5,(2|->4));
mv_right(7,(0|->4));
mv_up(2,(0|->2));
mv_right(13,(2|->2));
mv_up(10,(2|->0));
mv_up(10,(1|->0));
mv_up(10,(0|->0));
mv_right(13,(2|->3));
mv_up(1,(2|->1));
mv_up(1,(1|->1));
mv_up(1,(0|->1));
mv_left(13,(2|->1));
mv_left(6,(5|->0));
mv_down(3,(5|->2));
mv_left(12,(3|->2));
mv_down(11,(3|->5));
mv_right(7,(0|->5));
mv_left(12,(3|->1));
mv_left(12,(3|->0));
mv_up(4,(3|->3));
mv_up(4,(2|->3));
mv_up(4,(1|->3));
mv_up(4,(0|->3));
mv_right(13,(2|->3));
mv_down(1,(2|->1));
mv_right(12,(3|->3));
mv_down(10,(3|->0));
mv_right(12,(3|->4));
mv_down(1,(3|->1));
mv_down(10,(4|->0));
mv_left(9,(4|->3));
mv_down(1,(4|->1));
mv_left(13,(2|->1));
mv_down(4,(2|->3));
mv_left(7,(0|->3));
mv_left(8,(5|->3));
mv_up(11,(0|->5));
mv_right(12,(3|->5));
mv_up(3,(3|->2));
mv_right(6,(5|->2));
mv_down(10,(5|->0));
mv_left(13,(2|->0));
mv_down(2,(2|->2));
mv_left(7,(0|->2));
mv_up(5,(0|->4));
mv_left(7,(0|->1));
mv_up(4,(0|->3));
mv_left(7,(0|->0));
mv_up(2,(0|->2));
mv_right(13,(2|->2));
mv_up(10,(2|->0));
mv_right(13,(2|->3));
mv_right(13,(2|->4));
mv_left(6,(5|->0));
mv_down(3,(5|->2));
mv_left(12,(3|->2));
mv_down(11,(3|->5));
mv_down(11,(4|->5));
mv_down(11,(5|->5));
mv_right(13,(2|->5))


The full state space has 4782 states (including the root node and the set-up-constants node) and 29890 transitions, as indicated by ProB's coverage info (after doing full model checking without looking for states satisfying the GOAL predicate): 

STATES
deadlocked:0
invariant_violated:0
invariant_not_checked:0
open:0
live:4782
total:4782
TOTAL_OPERATIONS
29890
COVERED_OPERATIONS
INITIALISATION:1
SETUP_CONSTANTS:1
mv_down:8461
mv_left:6483
mv_right:6483
mv_up:8461
UNCOVERED_OPERATIONS

For reference, here are the statistics as output by TLC (when not looking for states satisfying the goal predicate): 

TLC2 Version 2.05 of 23 July 2013
Running in Model-Checking mode.
Parsing file /Users/leuschel/git_root/prob_examples/public_examples/B/Puzzles/RushHour_v2_TLC.tla
...
Semantic processing of module RushHour_v2_TLC
Starting... (2014-07-23 12:28:17)
Computing initial states...
Finished computing initial states: 1 distinct state generated.
Model checking completed. No error has been found.
  Estimates of the probability that TLC did not check all reachable states
  because two distinct states had the same fingerprint:
  calculated (optimistic):  val = 6.5E-12
  based on the actual fingerprints:  val = 8.0E-13
29889 states generated, 4780 distinct states found, 0 states left on queue.
The depth of the complete state graph search is 123.
Finished. (2014-07-23 12:28:21)
--------------------------------
Parsing time: 644 ms
Translation time: 107 ms
Model checking time: 3 sec
States analysed: 4780
Transitions fired: 29889
Result: NoError

Old Solution

This is my old solution to the Rush hour puzzle. It is not very elegant, but does work. It has a more sophisticated animation function for visualisation. 

MACHINE RushHour
/* not a very elegant model; but it seems to work */
/* ProB finds a solution for the hardest puzzle (no. 40) */
DEFINITIONS
  SET_PREF_MAXINT == 8;
  /*"RushHour/Puzzle10.def"; */
  "RushHour/Puzzle40.def";
  INDEX == (1..dim);
  GOAL == (pos_hcar(red_hcar) >= dim-size_hcar(red_hcar)+1);
  HEURISTIC_FUNCTION == dim-size_hcar(red_hcar) - pos_hcar(red_hcar) ; /* not a very interesting heuristic function; as red_car can only be moved at very last step */
  ANIMATION_IMG0 == "images/sm_empty_box.gif";
  ANIMATION_IMG1 == "images/sm_vcar.gif";
  ANIMATION_IMG2 == "images/sm_vcar_front.gif";
  ANIMATION_IMG3 == "images/sm_hcar.gif";
  ANIMATION_IMG4 == "images/sm_red_hcar.gif";
  ANIMATION_FUNCTION == ( {r,c,i|r:1..dim & c:1..dim & i=0}  <+
                          {r,c,i|r:1..dim & c:1..dim & i=1 &
                                 #j.(j:dom(col_vcar) & c=col_vcar(j) &
                                     r>pos_vcar(j) & r<pos_vcar(j)+size_vcar(j)) } <+
                          {r,c,i|r:1..dim & c:1..dim & i=2 &
                             #j.(j:dom(col_vcar) & c=col_vcar(j) & r=pos_vcar(j)) } <+
                          {r,c,i|r:1..dim & c:1..dim & i:3..4 &
                                 #j.(j:dom(row_hcar) & r=row_hcar(j) &
                                     c>=pos_hcar(j) & c<pos_hcar(j)+size_hcar(j) &
                                     ((j=red_hcar & i=4) or (j/=red_hcar & i=3)) ) }
                        );
                        
   POSs_VCAR(vc) == {c,r|c=col_vcar(vc) & r>=pos_vcar(vc) & r<pos_vcar(vc)+size_vcar(vc)};
   POSs_HCAR(hc) == {c,r|r=row_hcar(hc) & c>=pos_hcar(hc) & c<pos_hcar(hc)+size_hcar(hc)}
CONSTANTS
 vcars,hcars,dim, col_vcar, row_hcar, size_vcar, size_hcar,
 red_hcar
 
PROPERTIES

 /* The particular puzzle */
 STATIC_PROPS
 &

 dim = 6 &
 vcars : NATURAL1 & hcars: NATURAL1 &
 col_vcar: 1..vcars --> INDEX &
 row_hcar: 1..hcars --> INDEX &
 size_vcar: 1..vcars --> INDEX &
 size_hcar: 1..hcars --> INDEX &
 red_hcar : 1..hcars &
 
 /* vcars are in ascending in row order */
 !r.(r:1..(vcars-1) => col_vcar(r)<=col_vcar(r+1)) &
 /* hcars are in ascending in col order */
 !c.(c:1..(hcars-1) => row_hcar(c)<=row_hcar(c+1)) 
 
 
VARIABLES
  pos_vcar,
  pos_hcar
INVARIANT
  pos_vcar: 1..vcars --> INDEX &
  pos_hcar: 1..hcars --> INDEX
ASSERTIONS
  !(vc,hc).(vc:1..vcars &  hc:1..hcars => POSs_VCAR(vc) /\ POSs_HCAR(hc) = {});
  !(vc1,vc2).(vc1:1..(vcars-1) & vc2:2..vcars & vc1<vc2 => POSs_VCAR(vc1) /\ POSs_VCAR(vc2) = {});
  !(hc1,hc2).(hc1:1..(hcars-1) & hc2:2..hcars & hc1<hc2 => POSs_HCAR(hc1) /\ POSs_HCAR(hc2) = {})
  
INITIALISATION
  pos_vcar := INIT_VCAR ||
  pos_hcar := INIT_HCAR
OPERATIONS
  move_hcar_right(car) = 
    PRE car:1..hcars &
        pos_hcar(car)<=dim - size_hcar(car) & /* car not at extreme right */
       (car<hcars => (row_hcar(car) /= row_hcar(car+1) or
                     pos_hcar(car+1) > pos_hcar(car)+size_hcar(car))) &
       !cv.(cv:1..vcars & col_vcar(cv)=pos_hcar(car)+size_hcar(car) =>
             row_hcar(car) /: pos_vcar(cv)..pos_vcar(cv)+size_vcar(cv)-1)
       THEN
    pos_hcar(car) := pos_hcar(car)+1
  END;

  move_hcar_left(car) = 
    PRE car:1..hcars &
        pos_hcar(car)> 1 & /* car not at extreme left */
       (car>1 => (row_hcar(car) /= row_hcar(car-1) or
                  pos_hcar(car-1)+size_hcar(car-1) <= pos_hcar(car)-1))&
       !cv.(cv:1..vcars & col_vcar(cv)=pos_hcar(car)-1 =>
             row_hcar(car) /: pos_vcar(cv)..pos_vcar(cv)+size_vcar(cv)-1)
       THEN
    pos_hcar(car) := pos_hcar(car)-1
  END;
  
  
  move_vcar_down(car) = 
    PRE car:1..vcars &
        pos_vcar(car)<=dim - size_vcar(car) & /* car not at extreme bottom */
       (car<vcars => (col_vcar(car) /= col_vcar(car+1) or
                     pos_vcar(car+1) > pos_vcar(car)+size_vcar(car))) &
       !cv.(cv:1..hcars & row_hcar(cv)=pos_vcar(car)+size_vcar(car) =>
             col_vcar(car) /: pos_hcar(cv)..pos_hcar(cv)+size_hcar(cv)-1)
       THEN
    pos_vcar(car) := pos_vcar(car)+1
  END;

  move_vcar_up(car) = 
    PRE car:1..vcars &
        pos_vcar(car)> 1 & /* car not at extreme top */
       (car>1 => (col_vcar(car) /= col_vcar(car-1) or
                     pos_vcar(car-1)+size_vcar(car-1) <= pos_vcar(car)-1)) &
       !cv.(cv:1..hcars & row_hcar(cv)=pos_vcar(car)-1 =>
             col_vcar(car) /: pos_hcar(cv)..pos_hcar(cv)+size_hcar(cv)-1)
       THEN
    pos_vcar(car) := pos_vcar(car)-1
  END 
END


The encoding of hardest puzzle Nr 40 in the file RushHour/Puzzle40.def is as follows: 

DEFINITIONS
/* The particular puzzle (nr. 40) */
 STATIC_PROPS == 
 (vcars=7 & hcars = 6 &
 col_vcar =  {1|->1, 2|->2, 3|->3, 4|->3, 5|->4, 6|->5, 7|->6} & 
 size_vcar = {1|->3, 2|->2, 3|->2, 4|->2, 5|->2, 6|->2, 7|->3} &
 row_hcar =  {1|->1, 2|->3, 3|->4, 4|->5, 5|->6, 6|->6} &
 size_hcar = {1|->2, 2|->2, 3|->3, 4|->2, 5|->2, 6|->2} &
 red_hcar = 2); /* red hcar */
 INIT_VCAR == {1|->1, 2|->2, 3|->2, 4|->5, 5|->4, 6|->1, 7|->2 };
 INIT_HCAR == {1|->2, 2|->4, 3|->1, 4|->5, 5|->1, 6|->4}


ProB 1.3.7 took about 26 seconds to solve this puzzle (on my Mac Book Air 1.8 GHz i7; runtimes may vary as ProB uses a randomized depth-first/breadth-first search):


ProB RushHour Screenshot.png

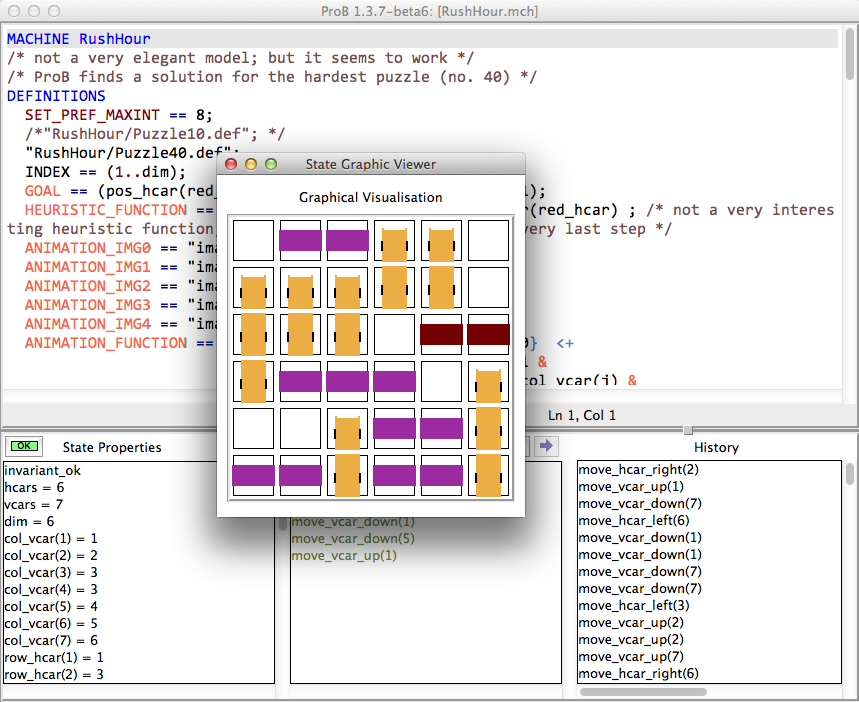
The solution found has 125 steps: 

SETUP_CONSTANTS(6,7,6,[1,2,3,3,4,5,6],[1,3,4,5,6,6],[3,2,2,2,2,2,3],[2,2,3,2,2,2],2)
INITIALISATION([1,2,2,5,4,1,2],[2,4,1,5,1,4])
move_hcar_right(6)
move_vcar_down(5)
move_hcar_right(3)
move_vcar_down(1)
move_vcar_up(7)
move_hcar_left(1)
move_vcar_down(1)
move_hcar_right(3)
move_vcar_down(2)
move_hcar_right(3)
move_vcar_down(2)
move_vcar_up(4)
move_vcar_up(3)
move_hcar_right(5)
move_vcar_down(1)
move_hcar_left(2)
move_vcar_down(6)
move_hcar_left(2)
move_hcar_left(2)
move_vcar_down(3)
move_hcar_right(1)
move_hcar_right(1)
move_hcar_right(1)
move_vcar_up(3)
move_hcar_right(2)
move_vcar_up(1)
move_vcar_up(1)
move_vcar_up(1)
move_hcar_right(2)
move_vcar_up(2)
move_vcar_up(2)
move_hcar_left(5)
move_vcar_down(4)
move_vcar_up(2)
move_hcar_left(3)
move_hcar_left(3)
move_hcar_left(3)
move_hcar_left(2)
move_vcar_up(5)
move_vcar_up(5)
move_vcar_up(5)
move_vcar_down(7)
move_hcar_right(1)
move_hcar_right(3)
move_vcar_up(5)
move_hcar_right(2)
move_vcar_down(1)
move_vcar_down(2)
move_hcar_right(3)
move_vcar_down(2)
move_vcar_down(2)
move_hcar_left(2)
move_vcar_down(5)
move_vcar_down(1)
move_hcar_left(1)
move_vcar_up(7)
move_hcar_right(3)
move_vcar_up(4)
move_hcar_right(5)
move_vcar_down(1)
move_hcar_left(2)
move_vcar_down(3)
move_hcar_left(1)
move_hcar_left(1)
move_hcar_left(1)
move_vcar_up(3)
move_hcar_right(2)
move_vcar_up(1)
move_hcar_left(5)
move_hcar_left(4)
move_vcar_up(5)
move_vcar_down(4)
move_hcar_right(2)
move_vcar_up(2)
move_vcar_up(6)
move_hcar_right(2)
move_vcar_up(1)
move_vcar_up(4)
move_vcar_up(4)
move_vcar_down(2)
move_vcar_down(1)
move_vcar_down(4)
move_vcar_down(3)
move_vcar_up(2)
move_vcar_up(2)
move_hcar_left(6)
move_hcar_right(1)
move_vcar_up(1)
move_vcar_up(1)
move_vcar_down(4)
move_vcar_down(3)
move_vcar_down(2)
move_vcar_down(2)
move_vcar_up(3)
move_vcar_up(4)
move_vcar_down(1)
move_vcar_down(1)
move_vcar_down(4)
move_vcar_up(2)
move_vcar_up(1)
move_hcar_left(3)
move_vcar_up(2)
move_vcar_down(7)
move_vcar_up(1)
move_vcar_down(7)
move_vcar_down(7)
move_vcar_down(2)
move_vcar_down(2)
move_vcar_up(7)
move_vcar_up(7)
move_hcar_right(6)
move_vcar_up(7)
move_vcar_up(2)
move_vcar_up(2)
move_hcar_left(3)
move_vcar_down(7)
move_vcar_down(7)
move_vcar_down(1)
move_vcar_down(1)
move_hcar_left(6)
move_vcar_down(7)
move_vcar_up(1)
move_hcar_right(2)


Adapted version for TLC

Using our translator to TLA+ we can solve an adapted version of the above model in 11 seconds plus the time for the translation and starting up the translator and TLC (a few seconds). (The model has to be rewritten slightly for TLC, as it's enumeration and constraint solving capabilities are more limited.)


ProB-TLC RushHour Screenshot.png


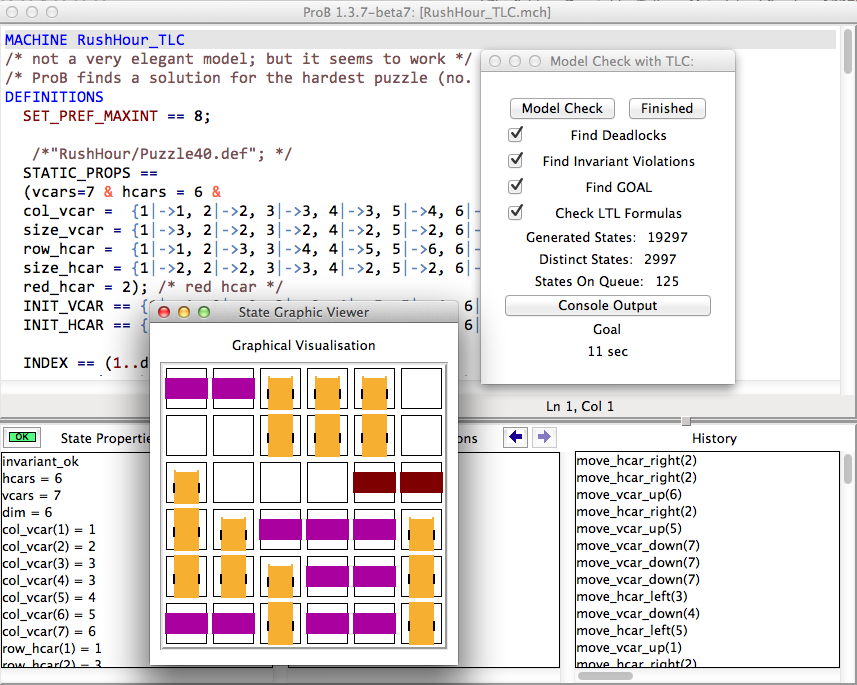
Here is the slightly rewritten version which works with TLC (in addition to ProB): 

MACHINE RushHour_TLC
/* not a very elegant model; but it seems to work */
/* ProB finds a solution for the hardest puzzle (no. 40) */
DEFINITIONS
  SET_PREF_MAXINT == 8;
  
   /*"RushHour/Puzzle40.def"; */
  STATIC_PROPS == 
  (vcars=7 & hcars = 6 &
  col_vcar =  {1|->1, 2|->2, 3|->3, 4|->3, 5|->4, 6|->5, 7|->6} & 
  size_vcar = {1|->3, 2|->2, 3|->2, 4|->2, 5|->2, 6|->2, 7|->3} &
  row_hcar =  {1|->1, 2|->3, 3|->4, 4|->5, 5|->6, 6|->6} &
  size_hcar = {1|->2, 2|->2, 3|->3, 4|->2, 5|->2, 6|->2} &
  red_hcar = 2); /* red hcar */
  INIT_VCAR == {1|->1, 2|->2, 3|->2, 4|->5, 5|->4, 6|->1, 7|->2 };
  INIT_HCAR == {1|->2, 2|->4, 3|->1, 4|->5, 5|->1, 6|->4};
  
  INDEX == (1..dim);
  GOAL == (pos_hcar(red_hcar) >= dim-size_hcar(red_hcar)+1);
  HEURISTIC_FUNCTION == dim-size_hcar(red_hcar) - pos_hcar(red_hcar) ; /* not a very interesting heuristic function; as red_car can only be moved at very last step */
  ANIMATION_IMG0 == "images/sm_empty_box.gif";
  ANIMATION_IMG1 == "images/sm_vcar.gif";
  ANIMATION_IMG2 == "images/sm_vcar_front.gif";
  ANIMATION_IMG3 == "images/sm_hcar.gif";
  ANIMATION_IMG4 == "images/sm_red_hcar.gif";
  ANIMATION_FUNCTION == ( {r,c,i|r:1..dim & c:1..dim & i=0}  <+
                          {r,c,i|r:1..dim & c:1..dim & i=1 &
                                 #j.(j:dom(col_vcar) & c=col_vcar(j) &
                                     r>pos_vcar(j) & r<pos_vcar(j)+size_vcar(j)) } <+
                          {r,c,i|r:1..dim & c:1..dim & i=2 &
                             #j.(j:dom(col_vcar) & c=col_vcar(j) & r=pos_vcar(j)) } <+
                          {r,c,i|r:1..dim & c:1..dim & i:3..4 &
                                 #j.(j:dom(row_hcar) & r=row_hcar(j) &
                                     c>=pos_hcar(j) & c<pos_hcar(j)+size_hcar(j) &
                                     ((j=red_hcar & i=4) or (j/=red_hcar & i=3)) ) }
                        );
                        
   POSs_VCAR(vc) == {c,r|c=col_vcar(vc) & r : pos_vcar(vc)..(pos_vcar(vc)+size_vcar(vc))-1}; /* r>=pos_vcar(vc) & r<pos_vcar(vc)+size_vcar(vc) */
   POSs_HCAR(hc) == {c,r|r=row_hcar(hc) & c : pos_hcar(hc) ..(pos_hcar(hc)+size_hcar(hc))-1} /*  c>=pos_hcar(hc) & c<pos_hcar(hc)+size_hcar(hc) */
CONSTANTS
 vcars,hcars,dim, col_vcar, row_hcar, size_vcar, size_hcar,
 red_hcar
 
PROPERTIES

 /* The particular puzzle */
 STATIC_PROPS
 &

 dim = 6 &
 vcars : NATURAL1 & hcars: NATURAL1 &
 col_vcar: 1..vcars --> INDEX &
 row_hcar: 1..hcars --> INDEX &
 size_vcar: 1..vcars --> INDEX &
 size_hcar: 1..hcars --> INDEX &
 red_hcar : 1..hcars &
 
 /* vcars are in ascending in row order */
 !r.(r:1..(vcars-1) => col_vcar(r)<=col_vcar(r+1)) &
 /* hcars are in ascending in col order */
 !c.(c:1..(hcars-1) => row_hcar(c)<=row_hcar(c+1)) 
 
 
VARIABLES
  pos_vcar,
  pos_hcar
INVARIANT
  pos_vcar: 1..vcars --> INDEX &
  pos_hcar: 1..hcars --> INDEX
ASSERTIONS
  !(vc,hc).(vc:1..vcars &  hc:1..hcars => POSs_VCAR(vc) /\ POSs_HCAR(hc) = {});
  !(vc1,vc2).(vc1:1..(vcars-1) & vc2:2..vcars & vc1<vc2 => POSs_VCAR(vc1) /\ POSs_VCAR(vc2) = {});
  !(hc1,hc2).(hc1:1..(hcars-1) & hc2:2..hcars & hc1<hc2 => POSs_HCAR(hc1) /\ POSs_HCAR(hc2) = {})
  
INITIALISATION
  pos_vcar := INIT_VCAR ||
  pos_hcar := INIT_HCAR
OPERATIONS
  move_hcar_right(car) = 
    PRE car:1..hcars &
        pos_hcar(car)<=dim - size_hcar(car) & /* car not at extreme right */
       (car<hcars => (row_hcar(car) /= row_hcar(car+1) or
                     pos_hcar(car+1) > pos_hcar(car)+size_hcar(car))) &
       !cv.(cv:1..vcars & col_vcar(cv)=pos_hcar(car)+size_hcar(car) =>
             row_hcar(car) /: pos_vcar(cv)..pos_vcar(cv)+size_vcar(cv)-1)
       THEN
    pos_hcar(car) := pos_hcar(car)+1
  END;

  move_hcar_left(car) = 
    PRE car:1..hcars &
        pos_hcar(car)> 1 & /* car not at extreme left */
       (car>1 => (row_hcar(car) /= row_hcar(car-1) or
                  pos_hcar(car-1)+size_hcar(car-1) <= pos_hcar(car)-1))&
       !cv.(cv:1..vcars & col_vcar(cv)=pos_hcar(car)-1 =>
             row_hcar(car) /: pos_vcar(cv)..pos_vcar(cv)+size_vcar(cv)-1)
       THEN
    pos_hcar(car) := pos_hcar(car)-1
  END;
  
  
  move_vcar_down(car) = 
    PRE car:1..vcars &
        pos_vcar(car)<=dim - size_vcar(car) & /* car not at extreme bottom */
       (car<vcars => (col_vcar(car) /= col_vcar(car+1) or
                     pos_vcar(car+1) > pos_vcar(car)+size_vcar(car))) &
       !cv.(cv:1..hcars & row_hcar(cv)=pos_vcar(car)+size_vcar(car) =>
             col_vcar(car) /: pos_hcar(cv)..pos_hcar(cv)+size_hcar(cv)-1)
       THEN
    pos_vcar(car) := pos_vcar(car)+1
  END;

  move_vcar_up(car) = 
    PRE car:1..vcars &
        pos_vcar(car)> 1 & /* car not at extreme top */
       (car>1 => (col_vcar(car) /= col_vcar(car-1) or
                     pos_vcar(car-1)+size_vcar(car-1) <= pos_vcar(car)-1)) &
       !cv.(cv:1..hcars & row_hcar(cv)=pos_vcar(car)-1 =>
             col_vcar(car) /: pos_hcar(cv)..pos_hcar(cv)+size_hcar(cv)-1)
       THEN
    pos_vcar(car) := pos_vcar(car)-1
  END 
END
Retrieved from "https://prob.hhu.de/w/index.php?title=Rush_Hour_Puzzle&oldid=4729"