Tutorial Modeling Infinite Datatypes

This tutorial describes how to model (and how not to model) infinite datatypes so that they can be animated with ProB. We illustrate this using a Stack datatype.

This does not work

MACHINE StackAxioms1
SETS Stack
CONSTANTS pop, push,empty
PROPERTIES
 empty:Stack &
 pop : Stack \ {empty} --> Stack &
!s,x . (s : Stack & x : NAT => pop(push(s |-> x)) = s) 
 & push: Stack*NAT --> Stack \ {empty}
END

To do: explain why: infinite Stack would be required; ProB does not support infinite deferred sets. We need to do a more constructive definition and use the infinite set ProB knows about: INTEGER.

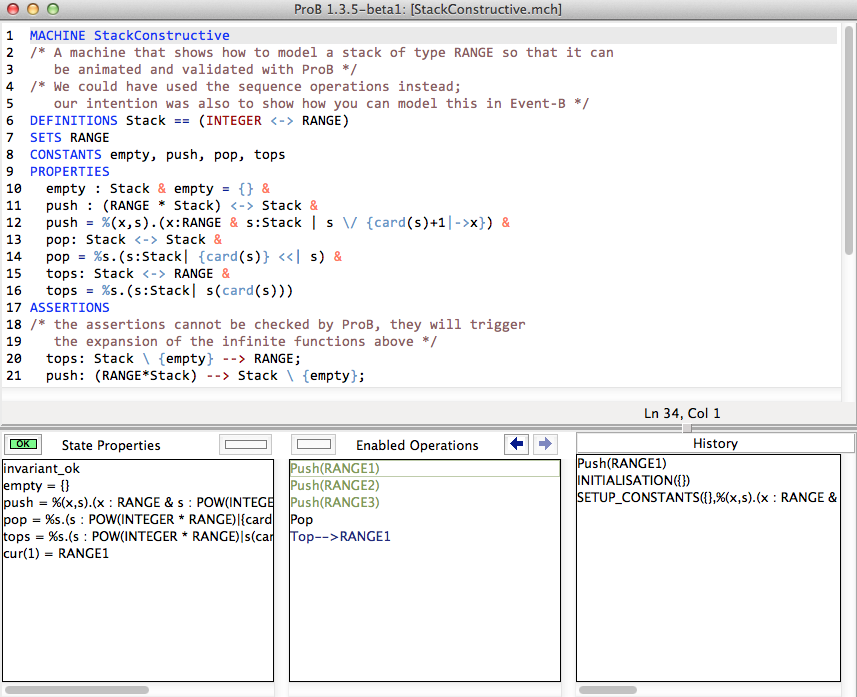
MACHINE StackConstructive
/* A machine that shows how to model a stack of type RANGE so that it can
   be animated and validated with ProB */
/* We could have used the sequence operations instead;
   our intention was also to show how you can model this in Event-B */
DEFINITIONS Stack == (INTEGER <-> RANGE)
SETS RANGE
CONSTANTS empty, push, pop, tops
PROPERTIES
  empty : Stack & empty = {} &
  push : (RANGE * Stack) <-> Stack &
  push = %(x,s).(x:RANGE & s:Stack | s \/ {card(s)+1|->x}) &
  pop: Stack <-> Stack &
  pop = %s.(s:Stack| {card(s)} <<| s) &
  tops: Stack <-> RANGE &
  tops = %s.(s:Stack| s(card(s)))
ASSERTIONS
/* the assertions cannot be checked by ProB, they will trigger
   the expansion of the infinite functions above */
  tops: Stack \ {empty} --> RANGE;
  push: (RANGE*Stack) --> Stack \ {empty};
  pop: Stack \ {empty} --> Stack
VARIABLES cur
INVARIANT
 cur: Stack 
 & cur : seq(RANGE) /* a slightly stronger invariant */
INITIALISATION cur := empty
OPERATIONS
  Push(yy) = PRE yy:RANGE THEN cur:= push(yy,cur) END;
  Pop = PRE cur /= empty THEN cur := pop(cur) END;
  t <-- Top = PRE cur /= empty THEN t := tops(cur) END
END

As the screenshot illustrates, this model can now be animated with ProB. Observe how the functions push, pop and tops are kept symbolic in the State View.