Tutorial Modeling Infinite Datatypes: Difference between revisions
Created page with '__NOTOC__ This tutorial describes how to model (and how not to model) infinite datatypes so that they can be animated with ProB. We illustrate this using a Stack datatype. This …' |
No edit summary |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
This tutorial describes how to model (and how not to model) infinite datatypes so that they can be animated with ProB. We illustrate this | This tutorial describes how to model (and how not to model) infinite datatypes so that they can be animated with ProB. | ||
(You may also want to look at the manual page on [[Recursively_Defined_Functions |recursive functions]].) | |||
We illustrate this by modeling a Stack datatype. | |||
Unfortunately, the following B machine does not work with ProB: | |||
MACHINE StackAxioms1 | MACHINE StackAxioms1 | ||
SETS Stack | SETS Stack | ||
| Line 13: | Line 15: | ||
END | END | ||
The problem with the above model is that the <tt>PROPERTIES</tt> can only be satisfied if <tt>Stack</tt> is infinite. However, ProB does not presently support infinite deferred sets. | |||
We need to do a more constructive definition and use the infinite set ProB knows about: <tt>INTEGER</tt>. This is done in the following machine, which is included in the <tt>examples/Tutorial</tt> directory of the [[Download|ProB distribution]]. | |||
MACHINE StackConstructive | MACHINE StackConstructive | ||
| Line 28: | Line 31: | ||
push = %(x,s).(x:RANGE & s:Stack | s \/ {card(s)+1|->x}) & | push = %(x,s).(x:RANGE & s:Stack | s \/ {card(s)+1|->x}) & | ||
pop: Stack <-> Stack & | pop: Stack <-> Stack & | ||
pop = %s.(s:Stack| {card(s)} <<| s) & | pop = %s.(s:Stack\ {empty} | {card(s)} <<| s) & | ||
tops: Stack <-> RANGE & | tops: Stack <-> RANGE & | ||
tops = %s.(s:Stack| s(card(s))) | tops = %s.(s:Stack\ {empty} | s(card(s))) | ||
ASSERTIONS | ASSERTIONS | ||
/* the assertions | /* the assertions can now be checked by ProB, they used to trigger | ||
the expansion of the infinite functions above */ | |||
tops: Stack \ {empty} --> RANGE; | tops: Stack \ {empty} --> RANGE; | ||
push: (RANGE*Stack) --> Stack \ {empty}; | push: (RANGE*Stack) --> Stack \ {empty}; | ||
| Line 47: | Line 50: | ||
t <-- Top = PRE cur /= empty THEN t := tops(cur) END | t <-- Top = PRE cur /= empty THEN t := tops(cur) END | ||
END | END | ||
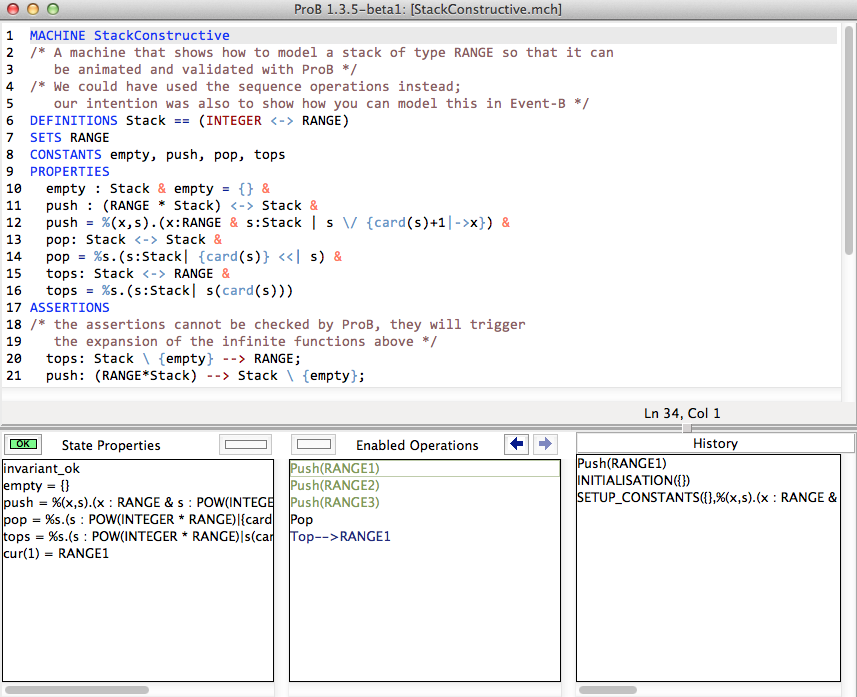
As the screenshot illustrates, this model can now be animated with ProB. Observe how the functions push, pop and tops are kept symbolic in the State View. | |||
[[File:StackConstructiveProB.png|500px]] | |||
Latest revision as of 13:08, 2 November 2023
This tutorial describes how to model (and how not to model) infinite datatypes so that they can be animated with ProB. (You may also want to look at the manual page on recursive functions.) We illustrate this by modeling a Stack datatype.
Unfortunately, the following B machine does not work with ProB:
MACHINE StackAxioms1
SETS Stack
CONSTANTS pop, push,empty
PROPERTIES
empty:Stack &
pop : Stack \ {empty} --> Stack &
!s,x . (s : Stack & x : NAT => pop(push(s |-> x)) = s)
& push: Stack*NAT --> Stack \ {empty}
END
The problem with the above model is that the PROPERTIES can only be satisfied if Stack is infinite. However, ProB does not presently support infinite deferred sets. We need to do a more constructive definition and use the infinite set ProB knows about: INTEGER. This is done in the following machine, which is included in the examples/Tutorial directory of the ProB distribution.
MACHINE StackConstructive
/* A machine that shows how to model a stack of type RANGE so that it can
be animated and validated with ProB */
/* We could have used the sequence operations instead;
our intention was also to show how you can model this in Event-B */
DEFINITIONS Stack == (INTEGER <-> RANGE)
SETS RANGE
CONSTANTS empty, push, pop, tops
PROPERTIES
empty : Stack & empty = {} &
push : (RANGE * Stack) <-> Stack &
push = %(x,s).(x:RANGE & s:Stack | s \/ {card(s)+1|->x}) &
pop: Stack <-> Stack &
pop = %s.(s:Stack\ {empty} | {card(s)} <<| s) &
tops: Stack <-> RANGE &
tops = %s.(s:Stack\ {empty} | s(card(s)))
ASSERTIONS
/* the assertions can now be checked by ProB, they used to trigger
the expansion of the infinite functions above */
tops: Stack \ {empty} --> RANGE;
push: (RANGE*Stack) --> Stack \ {empty};
pop: Stack \ {empty} --> Stack
VARIABLES cur
INVARIANT
cur: Stack
& cur : seq(RANGE) /* a slightly stronger invariant */
INITIALISATION cur := empty
OPERATIONS
Push(yy) = PRE yy:RANGE THEN cur:= push(yy,cur) END;
Pop = PRE cur /= empty THEN cur := pop(cur) END;
t <-- Top = PRE cur /= empty THEN t := tops(cur) END
END
As the screenshot illustrates, this model can now be animated with ProB. Observe how the functions push, pop and tops are kept symbolic in the State View.