Tutorial Disprover: Difference between revisions
No edit summary |
|||
| Line 35: | Line 35: | ||
Unfortunately, sometimes neither a counter example nor a proof can be found. | Unfortunately, sometimes neither a counter example nor a proof can be found. | ||
== Preferences == | |||
The disprover has a variety of preferences, shown below: | |||
[[File:DisproverPrefs.png]] | |||
Revision as of 08:42, 4 March 2022
WARNING
We believe the Disprover to be useful to find counter examples and avoid spending time to try and prove an unprovable proof obligation (PO). The disprover plugin can also be used as a prover, in case its search for counter examples is exhaustive. This, however, means that if your PO involves deferred sets (carrier sets which are not fixed) the disprover will never be able to prove it (as ProB only checks one particular cardinality of the deferred set). Please keep in mind, that you might run into some rough edges (please inform us about any issues).
Introduction
The ProB Disprover plugin for RODIN utilizes the ProB animator and model checker to automatically find counterexamples or proofs for a given proof obligation.
An early version of the ProB Disprover is described in Debugging Event-B Models using the ProB Disprover Plug-in, Ligot, Bendisposto, Leuschel.
Recently, the Disprover has been extended to detect cases in which the search for a counter-example was complete, yet there was no result. In this cases, the absence of a counter-example will be reported as a proof. See the paper describing the disprover as a prover for more details.
Installation
The ProB Disprover is currently only available through the ProB Nightly Build Update Site (http://nightly.cobra.cs.uni-duesseldorf.de/rodin/updatesite/).
How to use it
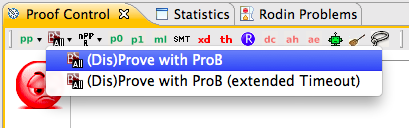
![]() : The proof obligation editor in Rodin presents the user with a number of Hypotheses and one Goal, to be proved. If the Disprover is installed, it is available in the tool bar alongside the other provers:
: The proof obligation editor in Rodin presents the user with a number of Hypotheses and one Goal, to be proved. If the Disprover is installed, it is available in the tool bar alongside the other provers:
How it works
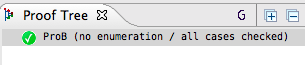
Upon selecting the Disprover, it builds a formula from the Hypotheses and the negated Goal. The ProB model checker then tries to find a model for that formula. If that is possible, this model is a counter example that will be presented back to the user in the proof tree. The disprover also checks if there cannot be a model for the formula. If this is the case it acts like a decision procedure, i.e., absence of a model is a proof for the goal. This is shown in the proof tree as follows:
Unfortunately, sometimes neither a counter example nor a proof can be found.
Preferences
The disprover has a variety of preferences, shown below: