Tutorial Debugging Well-Definedness and Transition Errors
We assume that you have grasped the way that ProB setups up the initial states of a B machine as outlined in Tutorial Setup Phases, and have understood why animation is difficult as outlined in Tutorial Understanding the Complexity of B Animation. You may also want to have a look at the explanation of well-definedness in B.
A simple example
Let us use the following B machine as starting point:
MACHINE WhileLoopInvariantError
VARIABLES xx
INVARIANT
xx:NATURAL
INITIALISATION xx:=1
OPERATIONS
Set(c) = PRE c:1..10 & xx<=c THEN
WHILE xx < c DO xx := xx+1
INVARIANT
xx <= c & xx:NATURAL &
xx<10 /* this is wrong */
VARIANT c-xx
END
END;
r <-- Get = BEGIN r:= xx END
END
After loading and initialising the machine you see that ProB has found a so-called "transition error", i.e., an error that occured while computing enabled operations (which correspond to a transition from one state to the B machine to another). These errors are displayed in red in the State Properties pane:
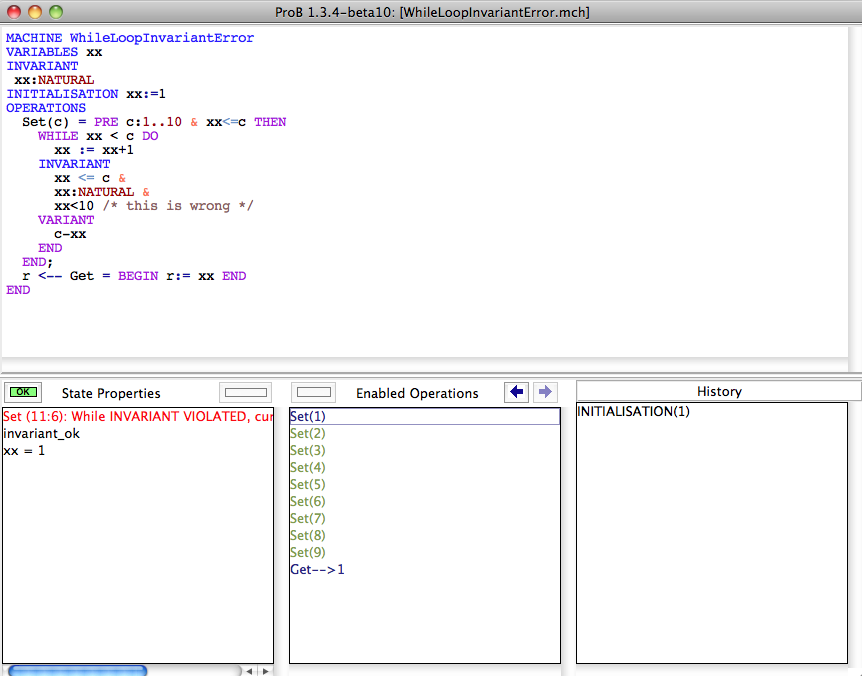
When you click on the red transition error you get presented with more details about the error:
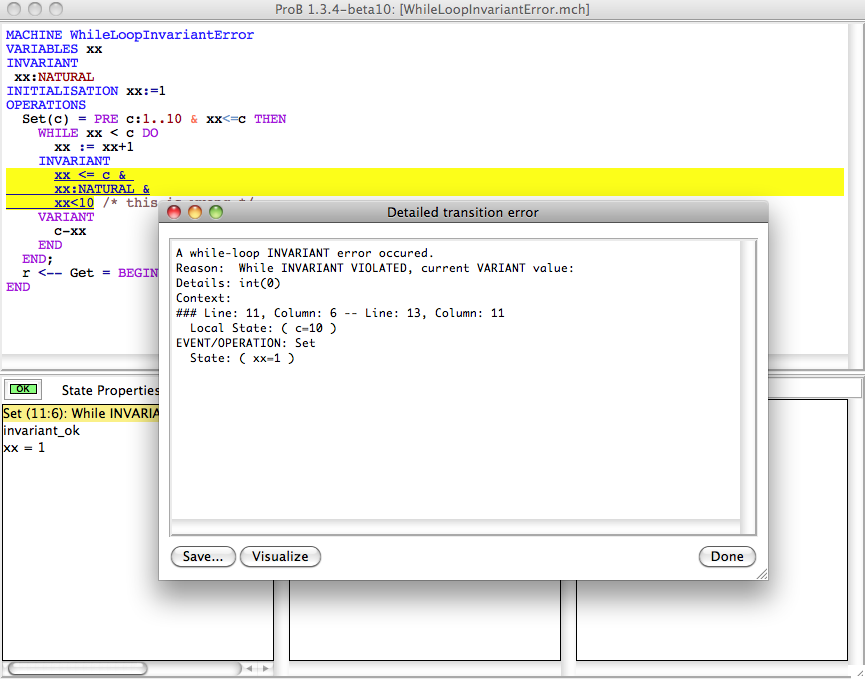
Sometimes you can also have the possibility to click on a "Visualise" button, which in this case will give you a graphical visualisation of the invariant violation:
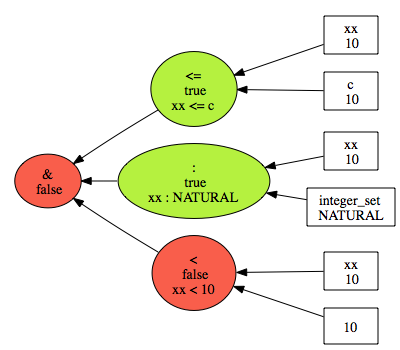
The same technique applies for inspecting other transition errors, such as:
- well-definedness errors of expressions such as:
- arithmetic well-definedness errors (division by 0, modulo by 0, modulo for negative numbers, min or max of empty set)
- functional well-definedness errors (function applied outside of domain or applied to relation,...)
- sequence well-definedness errors (first, last, tail, front of empt sequence,...)
- PRE condition errors (not for outermost preconditions, which are treated specially)
- ASSERT condition violations