Tutorial Complete Model Checking
We assume that you have completed Tutorial First Model Checking. There we have seen how to find invariant violations using the model checker.
In this part we use the following B Machine:
DEFINITIONS
MACHINE SimpleCounterForMC
DEFINITIONS MAX==4; SET_PREF_MAX_OPERATIONS==5
VARIABLES count
INVARIANT
count: 1..MAX
INITIALISATION count := 1
OPERATIONS
Increase(y) = PRE y: 1..(MAX-count) THEN
count := count+y
END;
Reset = BEGIN count :: 1..MAX END
END
To load this machine into ProB you can select "New..." from the "File" menu, choose a file name (e.g., "SimpleCounterForMC.mch") and then paste the text above into the ProB source pane and choose "Save and Reopen" from the "File" menu.
Note that the DEFINITION SET_PREF_MAX_OPERATIONS==5 means that ProB will compute at most 5 possible ways to execute any give operation (i.e., Increase and Reset in this case). We return to this issue below.
Successful Model Checking
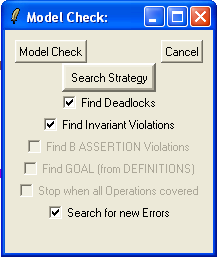
Now select the "Model Check..." command in the "Verify" menu which brings up the model checking dialog box:
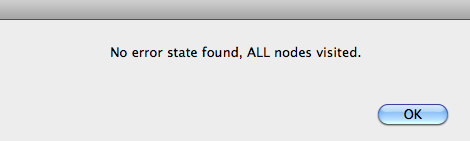
Now click the "Model Check" button. After a short while, ProB will give you the following message:
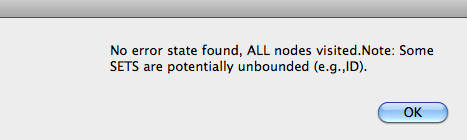
This message means that ProB has examine all possible states of your B model and has found no invariant violation and no deadlock. (In this case there are 4 states and one root node.)
Does this mean that the B machine is guaranteed to be correct? Does this mean that the AtelierB provers will be able to prove the B machine correct? In this case yes, but in general we have to be very careful about interpreting a completed model check. Below we examine several issues that have to be considered.
Computing All Transitions
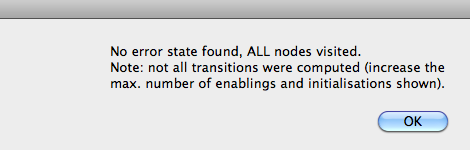
Let us now adapt the above B machine by changing the DEFINITION of MAX to 6. Now repeat the model checking exercise above. This time ProB will produce the following message:
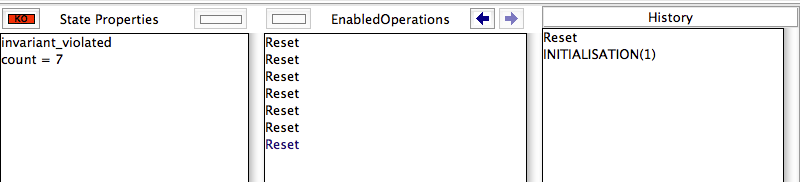
Again no invariant violations or deadlocks were found, but this time ProB warns us that not all transitions were computed. Indeed, the SET_PREF_MAX_OPERATIONS definition tells ProB to compute at most 5 ways to execute an operation. In this case, there are 6 ways to execute the Reset operation. As such, ProB may have missed certain states and thus may have missed an invariant violation.
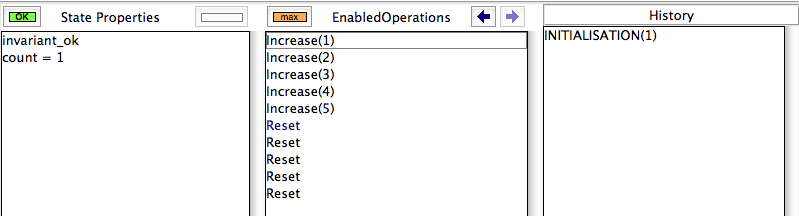
Indeed, when you double click on the "INITIALISATION(1)" entry in the "EnabledOperations" pane, you will see the following:
The orange "max" button tells us that not all operations were computed.
In this case, there was no error, but assume we change the definition of the Reset operation to
Reset = BEGIN count :: 1..MAX+1 END
and repeat the model checking. We will get the exact same result as above, but this time the machine is actually incorrect. The only way to solve ensure that ProB checks the entire state space is to increase the "MAX_OPERATIONS" preference to a suitably large value, e.g., SET_PREF_MAX_OPERATIONS==8 in this case. Now model checking will find a counter example:
Deferred Sets
Let us now use the following simple machine:
MACHINE SimpleCountDefSet
SETS ID
VARIABLES s
INVARIANT s <: ID & card(s)<10
INITIALISATION s := {}
OPERATIONS
Add(x) = PRE x:ID & x/:s THEN s := s\/{x} END;
Remove(x) = PRE x:s THEN s:= s - {x} END
END
Here model checking with ProB will give you the following message:
Unfortunately this does not guarantee that your machine is correct. Indeed, ProB has checked your machine only for one specific cardinality of the deferred set ID (probably 2 or 3). Indeed, if you look at the ProB window after loading the above machine you will see:
In the "State Properties" pane you can see that the cardinality of ID was set to 3. There are various ways you can influence the cardinality chosen by ProB; one is by adding a DEFINITION of the form:
DEFINITIONS scope_ID == 10
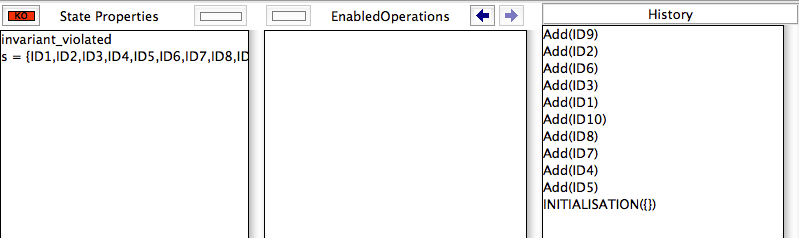
If you add this definition, ProB will now find an invariant violation:
However, if you remove the above DEFINITION and add the following instead:
PROPERTIES card(ID) = 5
ProB will give you the message we have already seen:
Indeed, you have now explicitly declare ID to be of size 5, and ProB has checked all states for that instantiation of ID. Another solution is to replace the deferred set ID by an enumerated set (this will, however, reduce the potential for symmetry reduction):
SETS ID={id1,id2,id3,id4,id5}
Infinite Types
It could be that your B machine makes use of the mathematical integers (INTEGER) or infinite subsets thereof (NATURAL, NATURAL1). Note that some derived types (such as seq(.)) are defined in terms of INTEGER. In this case there could be no way to explore all states of your system. For example, the following operation
Choose = BEGIN x :: NATURAL END
can be executed in infinitely many ways. ProB will in this case only find values between 0 and MAXINT for x. As such, a complete model checking does not indicate that your machine's state space has been fully explored. Note: ProB prints a warning on the console when an infinite type (like NATURAL) was "expanded" into a finite subset of it. This information is not yet fed back to the graphical user interface (but we are working on it).
Model Checking and Proof
Finally, even if ProB was able to successfully check the entire state space of your model, this does not imply that you can prove your machine correct with AtelierB (or Rodin). We dedicate another tutorial page to this:
Model Checking, Proof and CBC