The Jobs Puzzle: Difference between revisions
No edit summary |
Update link to ProB Logic Calculator |
||
| Line 36: | Line 36: | ||
To express ''"There are four people: Roberta, Thelma, Steve, and Pete”'' we define a set of people, that holds the list of names: | To express ''"There are four people: Roberta, Thelma, Steve, and Pete”'' we define a set of people, that holds the list of names: | ||
<pre>PEOPLE={"Roberta", "Thelma", "Steve", "Pete"}</pre> | <pre>PEOPLE={"Roberta", "Thelma", "Steve", "Pete"}</pre> | ||
We are using strings here to describe the elements of the set. This has the advantage, that the elements of the set are implicitly different.<ref>This encoding allows us to input the puzzle directly into the [ | We are using strings here to describe the elements of the set. This has the advantage, that the elements of the set are implicitly different.<ref>This encoding allows us to input the puzzle directly into the [[ProB Logic Calculator]].</ref> Alternatively, we could use enumerated or deferred sets defined in the SETS section of a B machine. | ||
As stated above we need some additional information that is not included in the puzzle to solve it. The first bit of information is that the names used in the puzzle imply the gender. In order to express this information we create two sets, MALE and FEMALE which are subsets of PEOPLE and contain the corresponding names. | As stated above we need some additional information that is not included in the puzzle to solve it. The first bit of information is that the names used in the puzzle imply the gender. In order to express this information we create two sets, MALE and FEMALE which are subsets of PEOPLE and contain the corresponding names. | ||
<pre>FEMALE={"Roberta", "Thelma"} & MALE={"Steve", "Pete"}</pre> | <pre>FEMALE={"Roberta", "Thelma"} & MALE={"Steve", "Pete"}</pre> | ||
Latest revision as of 13:56, 3 February 2021
Based on Michael Leuschel, David Schneider. Towards B as a High-Level Constraint Modeling Language. In Yamine Ait Amer, Klaus-Dieter Schewe (ed.): Abstract State Machines, Alloy, B, TLA, VDM, and Z, Springer Berlin Heidelberg, 8477: 101-116, 2014.
This puzzle was originally published in 1984 by Wos et al. [1] as part of a collection of puzzles for automatic reasoners. A reference implementation of the puzzle, by one of the authors of the book, using OTTER[2].
The puzzle consists of eight statements that describe the problem domain and provide some constraints on the elements of the domain. The problem is about a set of people and a set of jobs; the question posed by the puzzle is: who holds which job? The text of the puzzle as presented in "The jobs puzzle: A challenge for logical expressibility and automated reasoning."[3] is as follows:
- There are four people: Roberta, Thelma, Steve, and Pete.
- Among them, they hold eight different jobs.
- Each holds exactly two jobs.
- The jobs are: chef, guard, nurse, clerk, police officer (gender not implied), teacher, actor, and boxer.
- The job of nurse is held by a male.
- The husband of the chef is the clerk.
- Roberta is not a boxer.
- Pete has no education past the ninth grade.
- Roberta, the chef, and the police officer went golfing together.
What makes this puzzle interesting for automatic reasoners, is that not all the information required to solve the puzzle is provided explicitly in the text.
The puzzle can only be solved if certain implicit assumptions about the world are taken into account, such as: the names in the puzzle denote gender or that some of the job names imply the gender of the person that holds it.
Shapiro’s Challenge
Shapiro[3], following the original authors’ remarks, that formalizing the puzzle was at times hard and tedious, identified three challenges posed by the puzzle with regard to automatic reasoners. According to Shapiro, the challenges posed by the jobs puzzle are to:
- formalize it in a non-difficult, non-tedious way
- formalize it in a way that adheres closely to the English statement of the puzzle
- have an automated general-purpose commonsense reasoner that can accept that formalization and solve the puzzle quickly.
Any formalization also needs to encode the implicit knowledge used to solve the puzzle for the automatic reasoners while still trying to satisfy the aspects mentioned above. Addressing this challenge makes this puzzle a good case-study for the expressiveness of B to formalize such a problem.
A Solution to the Jobs Puzzle using B
The B encoding of the puzzle uses plain predicate logic, combined with set theory and arithmetic. We will show how this enables a very concise encoding of the problem, staying very close to the natural language requirements. Moreover, the puzzle can be quickly solved using the constraint solving capabilities of ProB. Following the order of the sentences in the puzzle we will discuss one or more possibilities to formalize them using B.
To express "There are four people: Roberta, Thelma, Steve, and Pete” we define a set of people, that holds the list of names:
PEOPLE={"Roberta", "Thelma", "Steve", "Pete"}
We are using strings here to describe the elements of the set. This has the advantage, that the elements of the set are implicitly different.[4] Alternatively, we could use enumerated or deferred sets defined in the SETS section of a B machine. As stated above we need some additional information that is not included in the puzzle to solve it. The first bit of information is that the names used in the puzzle imply the gender. In order to express this information we create two sets, MALE and FEMALE which are subsets of PEOPLE and contain the corresponding names.
FEMALE={"Roberta", "Thelma"} & MALE={"Steve", "Pete"}
The next statement of the puzzle is: “among them, they hold eight different jobs”. This can be formalized in B using a function that maps from a job to the corresponding person that holds this job using a total surjection from JOBS to PEOPLE:
HoldsJob : JOBS -->> PEOPLE
Although redundant, as we will see below, to express “Among them, they hold eight different jobs” we can add the assertion that the cardinality of HoldsJob is 8. This is possible, because in B functions and relations can be treated as sets of pairs, where each pair consists of an element of the domain and the corresponding element from the range of the relation.
card(HoldsJob) = 8
Constraining the jobs each person holds, the puzzle states: “Each holds exactly two jobs”. To express this we use the inverse relation of HoldsJob, it maps a PERSON to the JOBS associated to her. The inverse function or relation is expressed in B using the ~ operator. For readability we assign the inverse of HoldsJob to a variable called JobsOf. JobsOf is in this case is a relation, because, as stated above, each person holds two jobs.
JobsOf = HoldsJob~
Because JobsOf is a relation and not a function, in order to read the values, we need to use B’s relational image operator. This operator maps a subset of the domain to a subset of the range, instead of a single value. To read the jobs Steve holds, the relational image of JobsOf is used as shown below:
JobsOf[{"Steve"}]
Using the JobsOf relation we can express the third sentence of the puzzle using a universally quantified expression over the set PEOPLE. The Universal quantification operator (∀) is expressed in B using the ! symbol followed by the name of the variable that is quantified. This way of expressing the constraint is close to the original text of the puzzle, saying that the set of jobs each person holds has a cardinality of two.
!x.(x : PEOPLE => card(JobsOf[{x}]) = 2)
The fourth sentence assigns the set of job names to the identifier JOBS. This statement also constraints the cardinality of HoldsJob to 8.
JOBS = {"chef", "guard", "nurse", "clerk", "police", "teacher", "actor", "boxer"}
The following statements further constrain the solution. First “The job of nurse is held by a male”, which we can express using the HoldsJob function and the set MALE by stating that the element of PEOPLE that HoldsJob("nurse") points to is also an element of the set MALE.
HoldsJob("nurse") : MALE
Additionally, we add the next bit of implicit information, which is that typically a distinction is made between actress and actor, and therefore the job name actor implies that it is held by a male. This information is formalized, similarly as above.
HoldsJob("actor") : MALE
The next sentence: “The husband of the chef is the clerk” contains two relevant bits of information, based on another implicit assumption, which is that marriage usually is between one female and one male. With this in mind, we know that the chef is female and the clerk is male. One possibility is to do the inference step manually and encode this as:
HoldsJob("chef") : FEMALE & HoldsJob("clerk") : MALE
Alternatively, and in order to stay closer to the text of the puzzle we can add a function Husband that maps from the set FEMALE to the set MALE as a partial injection. We use a partial function, because we do not assume that all elements of FEMALE map to an element of MALE.
Husband : FEMALE >+> MALE
To add the constraint using this function we state that the tuple of the person that holds the job as chef and the person that holds the job as clerk are an element of this function when treated as a set of tuples.
(HoldsJob("chef"), HoldsJob("clerk")) : Husband
The next piece of information is that “Roberta is not a boxer”. Using the JobsOf relation we can express this close to the original sentence, by stating: boxer is not one of Roberta’s jobs. This can be expressed using the relational image of the JobsOf relation:
"boxer" /: JobsOf[{"Roberta"}]
The next sentence provides the information that “Pete has no education past the ninth grade”. This again needs some contextual information to be useful in order to find a solution for the puzzle[3]. To interpret this sentence we need to know that the jobs of police officer, teacher and nurse require an education of more than 9 years. Hence the information we get is that Pete does not hold any of these jobs. Doing this inference step we could, as above, state something along the lines of HoldsJob("police") /= "Pete", etc. for each of the jobs. The solution used here, tries to avoid doing the manual inference step. Although we still need to provide the information needed to draw the conclusion that Pete does not hold any of these three jobs. We create a set of those jobs that need higher education:
QualifiedJobs = {"police", "teacher", "nurse"}
Using the relational image operator we can now say that Pete is not among the ones that hold any of these jobs. The relational image can be used to get the set of items in the range of function or relation for all elements of a subset of the domain.
"Pete" /: HoldsJob[QualifiedJobs]
Finally, the last piece of information is that “Roberta, the chef, and the police officer went golfing together”, from this we can infer that Roberta, the chef, and the police officer are all different persons. We write this in B stating that the set of Roberta, the person that holds the job as chef, and the person that is the police officer has cardinality 3, using a variable for the set for readability.
Golfers = {"Roberta", HoldsJob("chef"), HoldsJob("police")} & card(Golfers) = 3
By building the conjunction of all these statements, ProB searches for a valid assignment to the variables introduced that satisfies all constraints, generating a valid solution that answers the question posed by the puzzle “who holds which job? ” in form of the HoldsJob function. The solution found by ProB is depicted below.
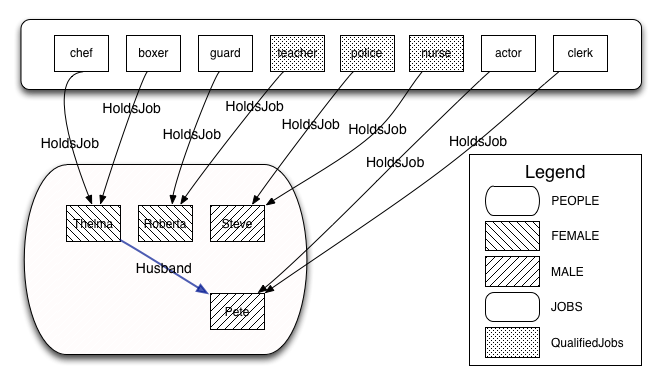
This satisfies, in our eyes, the challenges identified by Shapiro. In the sense that the formalization, is not difficult, although it uses a formal language. The elements of this language are familiar to most programmers or mathematicians and it builds upon well understood and widely known concepts. The brevity of the solution shows that using an expressive high-level language it is possible to encode the puzzle without having tedious tasks in order to be able to solve the puzzle at all. The encoding of the sentences follows the structure of the English statements very closely. We avoid the use of quantification wherever possible and use set based expressions that relate closely to the puzzle. We are able to encode the additional knowledge needed to solve puzzle in a straight forward way, that is also close to how this would be expressed as statements in English. Lastly it is worth to note that the formalization of “Each holds exactly two jobs” is the one furthest away from the English expression, using quantifications and set cardinality expressions.
Related Work
In his paper Shapiro discusses several formalizations of the puzzle with regard to the identified challenges. A further formalization using controlled natural language and answer set programming (ASP) was presented in "The jobs puzzle: Taking on the challenge via controlled natural language processing" by Schwitter et al.[5]
The first of the solutions discussed by Shapiro is a solution from the TPTP website, encoded as a set of clauses and translated to FOL. The main disadvantages of this encoding is that it requires 64 clauses to encode the problem and many of them are needed to define equality among jobs and names. This is in contrast to our B encoding using either enumerated sets or strings, where all elements are implicitly assumed to be different. Thus the user does not have to define the concept of equality for simple atoms.
The second solution discussed by Shapiro uses SNePS[6], a common sense and natural language reasoning system designed with the goal to “have a formal logical language that captured the expressibility of the English language”[3]. The language has a unique name assumption and set arguments making the encoding simpler and less tedious. On the other hand the lack of support for modus tolens requires rewriting some of the statements in order to solve the puzzle.
The last formalization discussed by Shapiro uses Lparse and Smodles[7] which uses stable model semantics with an extended logic programming syntax. According to Shapiro several features of Lparse/Smodels are simmilar to those of SNePS. This formalization also simplifies the encoding of the puzzle, but according to Schwitter et al. both solutions still present a “considerable conceptual gap between the formal notations and the English statements of the puzzle”[5].
Schwitter et al. in their paper “The jobs puzzle: Taking on the challenge via controlled natural language processing”[5] present a solution to the jobs puzzle using controlled natural language and a translation to ASP to solve the jobs puzzle in a novel way that stays very close to the English statements of the puzzle and satisfying the challenges posed by Shapiro. To avoid the mismatch between natural and controlled natural languages Schwitter et al. describe the use of a development environment that supports the user to input valid statements according to the rules of the controlled language. A solution using a mathematical, but high level language like B avoids this problems by having a formal and, for most, familiar language used to formalize the problem.
MACHINE JobsPuzzle
SETS
P = {Roberta, Thelma, Steve, Pete};
J = {chef, guard, nurse, clerk, police, teacher, actor, boxer}
CONSTANTS PEOPLE, JOBS, MALE, FEMALE, HoldsJob, Husband, QualifiedJobs, Golfers
PROPERTIES
/* There are four people: Roberta, Thelma, Steve, and Pete. */
PEOPLE={Roberta, Thelma, Steve, Pete}
&
/* Implicit assumption, names denote gender */
FEMALE={Roberta, Thelma} & MALE={Steve, Pete}
/* Among them, they hold eight different jobs. */
&
HoldsJob : JOBS -->> PEOPLE
/* Each holds exactly two jobs. */
&
!x.(x : PEOPLE => card(HoldsJob|>{x}) = 2)
&
JOBS = {chef, guard, nurse, clerk, police, teacher, actor, boxer}
/* The job of nurse is held by a male. */
&
HoldsJob(nurse) : MALE
/* Implicit assumption -> see slides (gender specific job-name (actor vs. actress?) */
&
HoldsJob(actor) : MALE
/* The husband of the chef is the clerk. */
&
Husband : FEMALE >+> MALE
&
(HoldsJob(chef), HoldsJob(clerk)) : Husband
/* Roberta is not a boxer. */
&
HoldsJob(boxer) /= Roberta
/* Pete has no education past the ninth grade. */
& /* Implicit assumption, these jobs require higher education */
QualifiedJobs = {police, teacher, nurse}
&
Pete /: HoldsJob[QualifiedJobs]
/* Roberta, the chef, and the police officer went golfing together. */
& Golfers = {Roberta, HoldsJob(chef), HoldsJob(police)} & card(Golfers) = 3
END
- ↑ L. Wos, R. Overbeek, E. Lusk, and J. Boyle. Automated Reasoning: Introduction and Applications. Prentice-Hall, Englewood Cliffs, NJ, 1984.
- ↑ W. Mccune. Otter 3.3 reference manual, 2003.
- ↑ 3.0 3.1 3.2 3.3 S. C. Shapiro. The jobs puzzle: A challenge for logical expressibility and automated reasoning. In AAAI Spring Symposium: Logical Formalizations of Commonsense Reasoning, 2011.
- ↑ This encoding allows us to input the puzzle directly into the ProB Logic Calculator.
- ↑ 5.0 5.1 5.2 R. Schwitter. The jobs puzzle: Taking on the challenge via controlled natural language processing. Theory and Practice of Logic Programming, 13:487–501, 7 2013.
- ↑ S. C. Shapiro and The SNePS Implementation Group. SNePS 2.7.1 User’s Manual. Department of Computer Science and Engineering University at Buffalo, The State University of New York, Dec. 2010.
- ↑ I. Niemelä, P. Simons, and T. Syrjänen. Smodels: A system for answer set programming. CoRR, cs.AI/0003033, 2000.