ProZ
ProZ is a extension of the ProB animator and model checker to support Z specifications. It uses the Fuzz Type Checker by Mike Spivey for extracting the formal specification from a LaTeX file. On the website you can also find documentation about the syntax of Z specifications. The iFM'07 article on ProZ contains more details about the implementation.
Preferences
A Z specification frequently makes use of comprehension sets, which are often introduced by the underlying translation process from Z to B. Normally those comprehension sets should be treated symbolically. To support this, you should set the following in the preferences menu:
Animation Preferences -> - Lazy expansion of lambdas & set comprehensions: True - Convert lazy form back into explicit form for Variables and Constants: False
Structure of the Z Specification
State and Initialization
To identify the components (like state, initialization, operations) of a Z specification, ProZ expects a certain structure of the specification: There must be a schema called "Init". "Init" describes the initialization of the state. "Init" must include exactly one schema in the declaration part. This schema is assumed to be the state schema.
For example, let S be the state schema (= is used for \defs):
S = [ x,y:N ]
There are two supported styles for the initialization:
a) Init = [ S | x=0 /\ y=1] b) Init = [ S'| x'=0 /\ y'=1 ]
If you want to use the logic of other schemas besides the state schema in the initialization, you can do that by including those schemas in the predicate part.
Operations
ProZ identifies schemas as operations if they satisfy the following properties:
- All variables of the state and their primed counterpart are declared in the operation. Usually this is done by including "\Delta S" in the operation (with S being the state schema).
- The operation is not referenced by any other schema in the specification
Example: Let S be defined as above:
A = [ \Delta S | x'=x+1 /\ y'=y ] B = [ x,y,x',y':N | x'=x+1 /\ y'=y ] C = [ x,x':N | x'=x+1 ] D = [ y,y':N | y'=y ] E = C /\ D F = [ \Xi S | x=0 ]
Then the schemas A,B and E describe all the same operation. F is also identified as an operation that leaves the state unchanged.
Axiomatic definitions
If axiomatic definitions are present, the declared variables are treated like constants. In the first step of the animation, ProB searches for values that satisfy all predicates of the axiomatic definitions are searched. After the first step, the predicates of the axiomatic definitions are ignored. If you want to define functions in an axiomatic definition, consider that ProB can treat lambda expressions and set comprehensions symbolically. Example: The definition of a function "square" could be
a)
| square : Z -> Z |----------------------- | square = (\lambda x:Z @ x*x)
b)
| square : Z -> Z |----------------------- | \forall x:Z @ square x = x*x
When using ProZ, it is preferable to use the method "a" because the lambda expression can be interpreted symbolically. If "b" is used, ProB will try to find a explicit set that will satisfy the given property.
Invariant
You can add a B-style invariant to the specification by defining a schema "Invariant" that declares a subset of the state variables. In each explored state the invariant will be checked. The model checking feature of ProB will try to find states that violate the invariant.
Scope
It is possible to limit the search space of the model checker by adding a schema "Scope" that declares a subset of the state variables. If such a schema is present, each explored state is checked, if it satisfies the predicate. If not, the state is not further explored.
Abbreviation Definitions
Abbreviation definitions (e.g. Abbr == {1,2,3}) are used like macros by ProZ. A reference to an abbreviation is replaced by its definition in a preprocessor phase. Thereby schemas defined by abbreviation definitions are ignored when ProZ tries to identify components. So, it is recommended to use schema definitions instead of abbreviation definitions (\defs instead of ==) when defining state, initialization, operations, etc.
Graphical animation
(Please note that this functionality is part of the next version. If you want to use graphical animation, please download a version from the Nightly build.)
Analogous to the graphical animation for B specifications, you can define a function that maps a coordinate to an image. Then ProZ will display the grid of images while animating the specification.
To use this feature, add a schema Proz_Settings that contains a variable animation\_function. The animation function should map a coordinate to an image. A coordinate is a pair of numbers or given sets.
The type used for images must be an enumerated set where the names of the elements denote their file names (without the suffix .gif).
Please see the specification jars.tex which is bundled with the ProB Tcl/Tk version for Download (inside the examples/Z/GraphicalAnimation/ directory). This is the part of the specification that defines the animation function (actually it defines a pair of animation functions: the default function over which the other function is overlaid; see Graphical_Visualization for more details):
We declare a type for the used images, the names of the elements refer to the file names of the GIF files.
\begin{zed}
Images ::= Filled | Empty | Void
\end{zed}
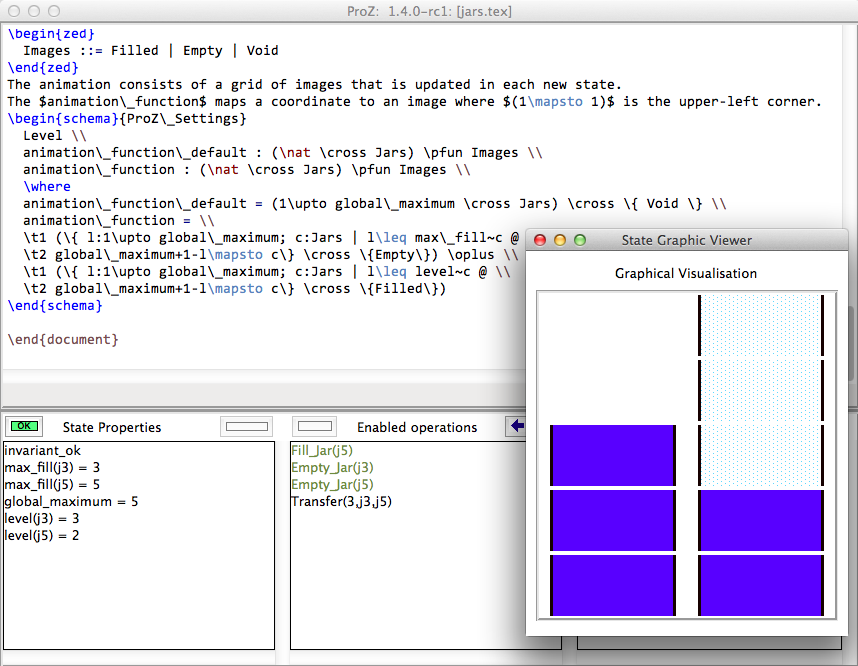
The animation consists of a grid of images that is updated in each new state.
The $animation\_function$ maps a coordinate to an image where $(1\mapsto 1)$ is the upper-left corner.
\begin{schema}{ProZ\_Settings}
Level \\
animation\_function\_default : (\nat \cross Jars) \pfun Images \\
animation\_function : (\nat \cross Jars) \pfun Images \\
\where
animation\_function\_default = (1\upto global\_maximum \cross Jars) \cross \{ Void \} \\
animation\_function = \\
\t1 (\{ l:1\upto global\_maximum; c:Jars | l\leq max\_fill~c @ \\
\t2 global\_maximum+1-l\mapsto c\} \cross \{Empty\}) \oplus \\
\t1 (\{ l:1\upto global\_maximum; c:Jars | l\leq level~c @ \\
\t2 global\_maximum+1-l\mapsto c\} \cross \{Filled\})
\end{schema}
Here is how the animation of the specification should look like:
Special constructs
prozignore
Sometimes it is not desired to check properties of some variables. E.g. ProZ checks if the square function in 2.3.a is a total function by enumerating it (it checks the function only for a limited interval). For more complex definitions the number of entries is often too large to check. When the user is sure that those properties are satisfied (like in our example), a solution is relaxing the declaration from "square : Z -> Z" to "square : Z <-> Z". Sometimes this is not easy to do, for instance if schema types are used which imply other constraints.
ProZ supports an operation \prozignore that instructs ProZ to ignore all constraints on the type and to use just the underlying type. For example, the square function could be defined by:
| square : \prozignore( Z -> Z ) |----------------------- | square = (\lambda x:Z @ x*x)
If you want to use \prozignore, you must first define a TeX command \prozignore:
\newcommand{\prozignore}{ignore_\textsl{\tiny ProZ}}
You can change the definition of the macro as you like because the content is ignored by ProZ. Then you must introduce a generic definition of \prozignore. The definition is ignored by ProB, but Fuzz needs it for type checking.
%%pregen \prozignore
\begin{gendef}[X]
\prozignore~\_ : \power X
\end{gendef}
It is also possible to append these lines to the "fuzzlib" in the fuzz distribution.
Translation to B
You can inspect the result of the translation process with "Show internal representation" in the "Debug" menu. Please note that the shown B machine is normally not syntactically correct because of
- additional constructs like free types
- additional type information of the form "var:type"
- names with primes (') or question marks, etc.
- lack of support from the pretty printer for every construct
Known Limitations
- Generic definitions are not supported yet.
- Miscellaneous unsupported constructs
- reflexive-transitive closure
- probably other?
- The error messages are not very helpful yet.
Summary of Supported Operators
Logical predicates:
-------------------
P \land Q conjunction
P \lor Q disjunction
P \implies Q implication
P \iff Q equivalence
\lnot P negation
Quantifiers:
------------
\forall x:T | P @ Q universal quantification (P => Q)
\exists x:T | P @ Q existential quantification (P & Q)
\exists_1 x:T | P @ Q exactly one existential quantification
Sets:
-----
\emptyset empty set
\{E,F\} set extension
\{~x:S | P~\} set comprehension
E \in S element of
E \notin S not element of
S \cup T union
S \cap T intersection
S \setminus T set difference
\power S power set
\# S cardinality
S \subseteq T subset predicate
S \subset T strict subset
\bigcup A generalized union of sets of sets
\bigcap A generalized intersection of sets of sets
Pairs:
------
E \mapsto F pair
S \cross T Cartesian product
first E first part of pair
second E second part of pair
Numbers:
--------
\nat Natural numbers
\num Integers
\nat_1 Positive natural numbers
m < n less
m \leq n less equal
m > n greater
m \geq n greater equal
m + n addition
m - n difference
m * n multiplication
m \div n division
m \mod n modulo**
m \upto n m..n
min S minimum of a set
max S maximum of a set
succ n successor of a number
**: modulo of negative numbers not supported
Functions:
----------
S \rel T relations
S \pfun T partial functions from S to T
S \fun T total functions from S to T
S \pinj T partial injections from S to T
S \inj T total injections from S to T
S \bij T total bijections from S to T
\dom R domain
\ran R range
\id S identity relation over S
S \dres R domain restriction
S \ndres R domain anti-restriction
R \rres S range restriction
R \nrres S range anti-restriction
R \oplus Q overriding
R \plus transitive closure
Sequences:
----------
\langle E,... \rangle explicit sequence
\seq S sequences over S
\seq_1 S non-empty sequences
\iseq S injective sequences over S
rev E reverse a sequence
head E first element of a sequence
last E last element of a sequence
tail E sequence with first element removed
front E all but the last element
E \cat F concatenation of two sequences
\dcat ss concatenation of sequences of sequences
E \filter F subsequence of elements of sequence E contained in set F
E \extract F extract subsequence from F with indexes in set E
squash F compaction
E \prefix F sequence E is a prefix of F
E \suffix F sequence E is a suffix of F
E \inseq F E is a sequence occuring in the middle of F (segment relation)
\disjoint E family of sets E is disjoint
E \partition F family of sets E is a partition of set F
Bags:
----------
\bag S bags over S
\lbag E,... \rbag explicit bag
count B E count of occurences of E in bag B
B \bcount E infix version of count
E \inbag B bag membership
B \subbageq C sub-bag relation
B \uplus C bag union
B \uminus C bag difference
items E bag of items in a sequence
n \otimes B bag scaling
Other:
-----------
\IF P \THEN E \ELSE F if-then-else expression
(\LET x == E @ F) Let-expression