Peaceable Armies of Queens: Difference between revisions
No edit summary |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
I found this challenging constraint programming problem in the following paper: | I found this challenging constraint programming problem in the following paper: | ||
* B. M. Smith, K. E. Petrie, and I. P. Gent. Models and symmetry breaking for peaceable armies of queens. In Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, pages 271–286. Springer Berlin Heidelberg, 2004. | * B. M. Smith, K. E. Petrie, and I. P. Gent. Models and symmetry breaking for peaceable armies of queens. In Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, pages 271–286. Springer Berlin Heidelberg, 2004. | ||
A variation of the problem can be found on page 329 of the Handbook on Constraint | A variation of the problem can be found on page 329 of the [https://www.elsevier.com/books/handbook-of-constraint-programming/rossi/978-0-444-52726-4 Handbook on Constraint Programming]. | ||
The challenge is to place two equal-sized armies of white and black queens onto a chessboard. | The challenge is to place two equal-sized armies of white and black queens onto a chessboard. | ||
We can distinguish between two problems: | We can distinguish between two problems: | ||
* <em>checking</em> whether two armies of <b>n</b> queens can be placed on a <b>dim*dim</b> chessboard, | * <em>checking</em> whether two armies of <b>n</b> queens can be placed on a <b>dim*dim</b> chessboard, | ||
* for a | * for a given board of size <b>dim*dim</b> find the maximal size <b>n</b> of armies that can be placed onto the board, i.e., solving an <em>optimisation</em> problem. | ||
== Checking == | == Checking == | ||
Here is a B model for the checking problem. The problem is quite straightforward to encode in B. | Here is a B model for the checking problem. The problem is quite straightforward to encode in B. | ||
Many lines below (in the DEFINITIONS) just define the animation function to graphically represent solutions. | Many lines below (in the DEFINITIONS) just define the [[Graphical_Visualization|animation function to graphically represent solutions]]. | ||
<pre> | <pre> | ||
| Line 50: | Line 50: | ||
</pre> | </pre> | ||
Here are some running times on my MacBook Air 1.7 GHz i7, also comparing to using [[Using_ProB_with_KODKOD | Kodkod as ProB's backend]] and using an [ | Here are some running times on my MacBook Air 1.7 GHz i7, also comparing to using [[Using_ProB_with_KODKOD | Kodkod as ProB's backend]] and using an [https://alloytools.org Alloy] model (see below). | ||
<pre> | <pre> | ||
dim=7, n=7 : solved in 0.3 secs | dim=7, n=7 : solved in 0.3 secs | ||
| Line 67: | Line 67: | ||
=== The Alloy model for comparison === | === The Alloy model for comparison === | ||
Here is the [ | Here is the [https://alloytools.org Alloy] model we have used. | ||
Initially, the model gave us wrong solutions as we were using <tt>+</tt> instead of <tt>sum</tt>; this was correct for previous versions of Alloy but not for Alloy 4.2 which we were using. | Initially, the model gave us wrong solutions as we were using <tt>+</tt> instead of <tt>sum</tt>; this was correct for previous versions of Alloy but not for Alloy 4.2 which we were using. | ||
Latest revision as of 16:33, 27 January 2021
I found this challenging constraint programming problem in the following paper:
- B. M. Smith, K. E. Petrie, and I. P. Gent. Models and symmetry breaking for peaceable armies of queens. In Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, pages 271–286. Springer Berlin Heidelberg, 2004.
A variation of the problem can be found on page 329 of the Handbook on Constraint Programming.
The challenge is to place two equal-sized armies of white and black queens onto a chessboard. We can distinguish between two problems:
- checking whether two armies of n queens can be placed on a dim*dim chessboard,
- for a given board of size dim*dim find the maximal size n of armies that can be placed onto the board, i.e., solving an optimisation problem.
Checking
Here is a B model for the checking problem. The problem is quite straightforward to encode in B. Many lines below (in the DEFINITIONS) just define the animation function to graphically represent solutions.
MACHINE JustQueens
DEFINITIONS
SET_PREF_TIME_OUT == 1000000;
SET_PREF_MAX_INITIALISATIONS == 1;
ANIMATION_IMG0 == "images/sm_empty_box.gif";
ANIMATION_IMG1 == "images/sm_gray_box.gif";
ANIMATION_IMG2 == "images/sm_queen_white.gif";
ANIMATION_IMG3 == "images/sm_queen_black.gif";
ANIMATION_IMG4 == "images/sm_knight_white.gif";
ANIMATION_IMG5 == "images/sm_knight_black.gif";
ANIMATION_IMG6 == "images/sm_white_queen_white.gif";
ANIMATION_IMG7 == "images/sm_white_queen_black.gif";
BWOFFSET(xx,yy) == (xx+yy) mod 2;
ANIMATION_FUNCTION_DEFAULT == ( {r,c,i|r:1..dim & c:1..dim & i=(r+c) mod 2 } );
ANIMATION_FUNCTION == ( UNION(k).(k:1..n| {(blackc(k),blackr(k),2+BWOFFSET(blackc(k),blackr(k)))}) \/
UNION(k).(k:1..n| {(whitec(k),whiter(k),6+BWOFFSET(whitec(k),whiter(k)))}) );
ORDERED(c,r) == (!i.(i:1..(n-1) => c(i) <= c(i+1)) &
!i.(i:1..(n-1) => (c(i)=c(i+1) => r(i) < r(i+1))))
CONSTANTS n, dim, blackc, blackr, whitec, whiter
PROPERTIES
n = 8 & dim = 8 &
blackc : 1..n --> 1..dim &
whitec : 1..n --> 1..dim &
blackr : 1..n --> 1..dim &
whiter : 1..n --> 1..dim &
ORDERED(blackc,blackr) & /* ensures proper ordering + that we do not place two queens on same square */
ORDERED(whitec,whiter) &
!(i,j).(i:1..n & j:1..n => blackc(i) /= whitec(j)) &
!(i,j).(i:1..n & j:1..n => blackr(i) /= whiter(j)) &
!(i,j).(i:1..n & j:1..n => blackr(i) /= whiter(j) + (blackc(i)-whitec(j))) &
!(i,j).(i:1..n & j:1..n => blackr(i) /= whiter(j) - (blackc(i)-whitec(j))) &
whitec(1) < blackc(1) /* symmetry breaking */
END
Here are some running times on my MacBook Air 1.7 GHz i7, also comparing to using Kodkod as ProB's backend and using an Alloy model (see below).
dim=7, n=7 : solved in 0.3 secs dim=7, n=8 : unsat in 20 secs dim=8, n=6 : solved in 0.02 secs (1.12 secs with Kodkod) dim=8, n=7 : solved in 0.06 secs (2.66 secs with Kodkod) dim=8, n=8 : solved in 0.53 secs (8.44 secs with Kodkod; 7.03 secs second run; +/- 8.5 with Alloy & miniSat; 9.3 seconds if we avoid overflows) dim=8, n=9 : solved in 12.96 secs (128.07 secs with Kodkod ; +/- 84 secs with Alloy & miniSat) dim=8, n=10 : unsat in 728 secs (Alloy & miniSat still running after over four hours)
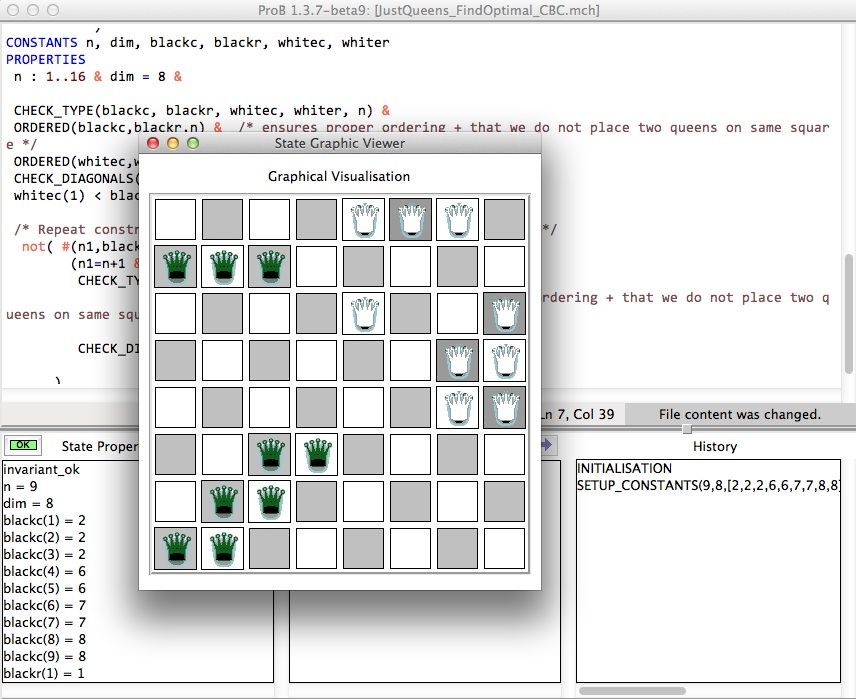
The first solution found for dim=8 and n=9 is as follows:
The Alloy model for comparison
Here is the Alloy model we have used. Initially, the model gave us wrong solutions as we were using + instead of sum; this was correct for previous versions of Alloy but not for Alloy 4.2 which we were using.
abstract sig Queens {
row : one Int,
col: one Int,
} {
row >= 0 and row < 8
and col >= 0 and col < 8
}
sig BQueens extends Queens {} {}
sig WQueens extends Queens {} {}
pred nothreat(q1,q2 : Queens) {
q1.row != q2.row
and q1.col != q2.col
and plus[ int[q1.row] , int[q1.col]] != plus[ int[q2.col] , int[q2.row]]
and plus [int[q1.row] , int[q2.col]] != plus[ int[q1.col] , int[q2.row]]
}
pred nothreats { all q1:BQueens, q2:WQueens |
nothreat[q1, q2]
}
pred alldiffB { all q1:BQueens, q2:BQueens |
q1=q2 or q1.row != q2.row or q1.col != q2.col
}
pred alldiffW { all q1:WQueens, q2:WQueens |
q1=q2 or q1.row != q2.row or q1.col != q2.col
}
pred equalnum {
#(WQueens) = #(BQueens)
}
pred valid {
nothreats and equalnum and alldiffB and alldiffW
}
fact {
#Queens = 16
}
run valid for 16 Queens, 7 int
Optimization
One can obviously use the above models to try and manually find a maximal value of n for a given board size dim. Below, we have encoded this process as B constraints, by setting up the problem twice: once for the army size n and a second time for army size n+1. The second encoding is wrapped into a negated existential quantification. (This model can no longer be translated into Kodkod because of this.)
ProB solves this optimisation problem in about 780 seconds for a board size of 8. This is very competitive with the timings reported in the above mentioned constraint solving paper using new symmetry breaking techniques and much more low-level encoding on state of the art constraint solving libraries such as ILOG.
MACHINE JustQueens_FindOptimal_CBC
DEFINITIONS
SET_PREF_TIME_OUT == 1000000;
SET_PREF_MAX_INITIALISATIONS == 1;
ANIMATION_IMG0 == "images/sm_empty_box.gif";
ANIMATION_IMG1 == "images/sm_gray_box.gif";
ANIMATION_IMG2 == "images/sm_queen_white.gif";
ANIMATION_IMG3 == "images/sm_queen_black.gif";
ANIMATION_IMG4 == "images/sm_knight_white.gif";
ANIMATION_IMG5 == "images/sm_knight_black.gif";
ANIMATION_IMG6 == "images/sm_white_queen_white.gif";
ANIMATION_IMG7 == "images/sm_white_queen_black.gif";
BWOFFSET(xx,yy) == (xx+yy) mod 2;
ANIMATION_FUNCTION_DEFAULT == ( {r,c,i|r:1..dim & c:1..dim & i=(r+c) mod 2 } );
ANIMATION_FUNCTION == ( UNION(k).(k:1..n| {(blackc(k),blackr(k),2+BWOFFSET(blackc(k),blackr(k)))}) \/
UNION(k).(k:1..n| {(whitec(k),whiter(k),6+BWOFFSET(whitec(k),whiter(k)))}) );
ORDERED(c,r,nn) == (!i.(i:1..(nn-1) => c(i) <= c(i+1)) &
!i.(i:1..(nn-1) => (c(i)=c(i+1) => r(i) < r(i+1))));
CHECK_TYPE(bc,br,wc,wr,nn) == (
bc : 1..nn --> 1..dim &
wc : 1..nn --> 1..dim &
br : 1..nn --> 1..dim &
wr : 1..nn --> 1..dim );
CHECK_DIAGONALS(bc,br,wc,wr,nn) == (
!(i,j).(i:1..nn & j:1..nn => bc(i) /= wc(j)) &
!(i,j).(i:1..nn & j:1..nn => br(i) /= wr(j)) &
!(i,j).(i:1..nn & j:1..nn => br(i) /= wr(j) + (bc(i)-wc(j))) &
!(i,j).(i:1..nn & j:1..nn => br(i) /= wr(j) - (bc(i)-wc(j)))
)
CONSTANTS n, dim, blackc, blackr, whitec, whiter
PROPERTIES
n : 1..16 & dim = 8 &
CHECK_TYPE(blackc, blackr, whitec, whiter, n) &
ORDERED(blackc,blackr,n) & /* ensures proper ordering + that we do not place two queens on same square */
ORDERED(whitec,whiter,n) &
CHECK_DIAGONALS(blackc, blackr, whitec, whiter, n) &
whitec(1) < blackc(1) /* symmetry breaking */ &
/* Repeat constraints for n+1 and assert that it cannot be solved */
not( #(n1,blackc1, blackr1, whitec1, whiter1).
(n1=n+1 & /* n1:2..17 & */
CHECK_TYPE(blackc1, blackr1, whitec1, whiter1, n1) &
ORDERED(blackc1,blackr1,n1) & /* ensures proper ordering + that we do not place two queens on same square */
ORDERED(whitec1,whiter1,n1) &
CHECK_DIAGONALS(blackc1, blackr1, whitec1, whiter1, n1) &
whitec1(1) < blackc1(1) /* symmetry breaking */
)
)
END
Here are the solving times for various board sizes on my MacBook Air:
dim=5 --> optimum n=4 found in 0.18 secs dim=6 --> optimum n=5 found in 1.16 secs dim=7 --> optimum n=7 found in 21.174 secs dim=8 --> optimum n=9 found in 780.130 secs
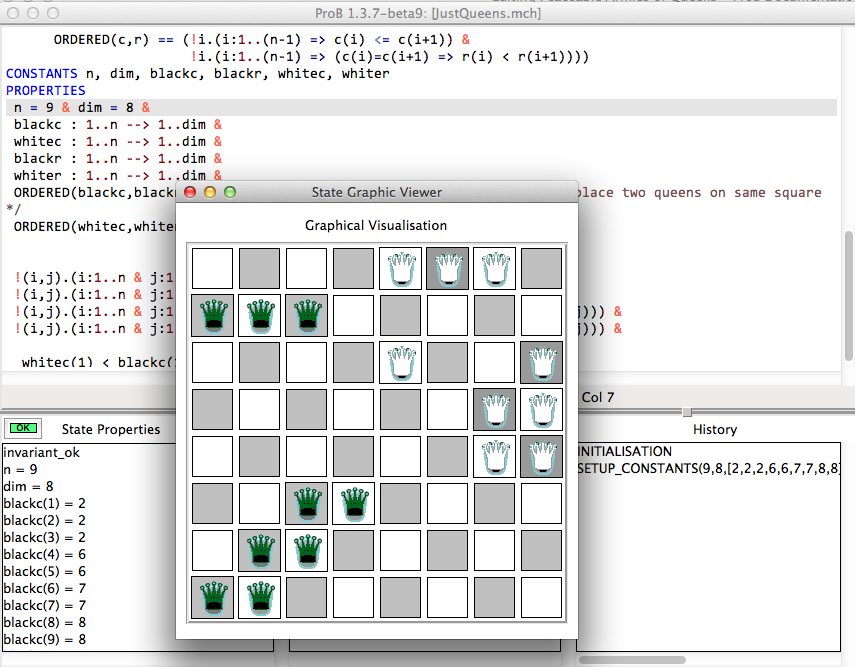
The first solution found for dim=8 is as follows: