LTL Model Checking: Difference between revisions
No edit summary |
|||
| Line 47: | Line 47: | ||
=== Supported Syntax === | === Supported Syntax === | ||
ProB supports LTL<sup>e</sup>, an extended version of LTL. In contrast to the standard LTL, LTL<sup>e</sup> provides support | ProB supports LTL<sup>[e]</sup>, an extended version of LTL. In contrast to the standard LTL, LTL<sup>[e]</sup> provides also support for propositions on transitions, not only on states. In practice, writing propositions on transitions is allowed by using the constructs `e(...)` and `[...]`. (see below). The LTL model checker of ProB supports Past-LTL<sup>[e]</sup> as well. | ||
* Atomic propositions can be one of the following: | * Atomic propositions can be one of the following: | ||
Revision as of 15:58, 20 November 2014
ProB provides support for LTL (linear temporal logic) model checking. For an introduction to LTL see the Wikipedia Article.
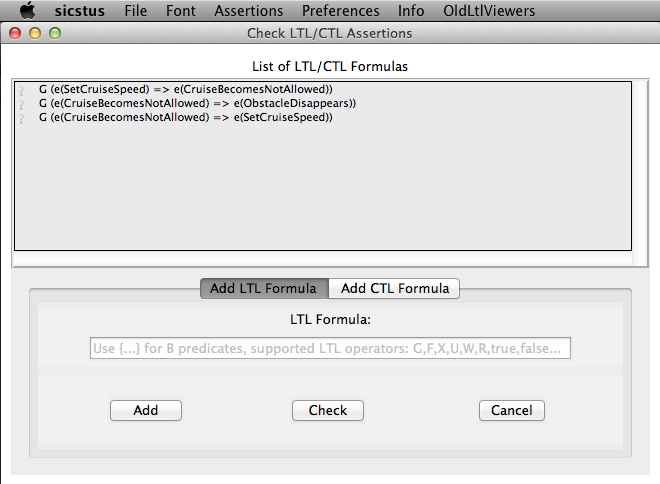
To use this feature, select "Check LTL/CTL Assertions" in the "Verify" menu. The feature can also be accessed by the key combination "Ctrl+L" under Windows and Linux, and by the key combination "Cmd+L" under MacOS. The following window appears:
All LTL formulas that are given in the "DEFINTIONS" section of a B machine are displayed in the list box of the LTL/CTL Assertions Viewer. For CSP-M specifications all LTL formulas given in the LTL pragmas of the loaded CSP-M file will be shown in the viewer. (For more detailed information of how LTL/CTL assertions can be stored into B and CSP-M models see Section Storing LTL Assertions into a Model).
A new LTL formula can be entered in the entry below the list box. (We explain the supported syntax below). The typed formula can then be either added to the list box by clicking the "Add" button or directly checked by clicking the "Check" button. Before doing that assure whether you are in the proper frame ("Add LTL Formula") of the bottom part of the LTL viewer.
The LTL model checker can be started for an LTL formula by performing a double-click on the respective formula or typing "Enter" after selecting the respective formula. Each LTL formula in the list box has on the left hand side a symbol that indicates what the status of the respective formula is. An LTL formula can have one of the following statuses (status symbols may differ under different operating systems):
- ? – The formula has not been checked yet.
- ✔ – The formula is true for all valid paths.
- ✘ – A counterexample for the formula has been found, i.e. there is a path that violates the formula. In case the formula has been just checked on the model the animator is navigated to the last state of the counterexample. The full path can then be seen in the history. The counterexample can be also obtained by the dotty-viewer after a second double-click on the formula in the assertions’ viewer.
- ⌚ – The formula is currently checked.
- ! – The formula check has been aborted by an unexpected error occurrence.
- ∞ – The formula check is incomplete, i.e. no counterexample was found so far, but the absence of a path that does not satisfy the formula can not be guaranteed because the state space was not fully explored. A new check can be started by a double-click.
All formulas can be checked by "Assertions -> Check All Assertions" in the menu bar. All formulas will be then checked from top to bottom in the list box.
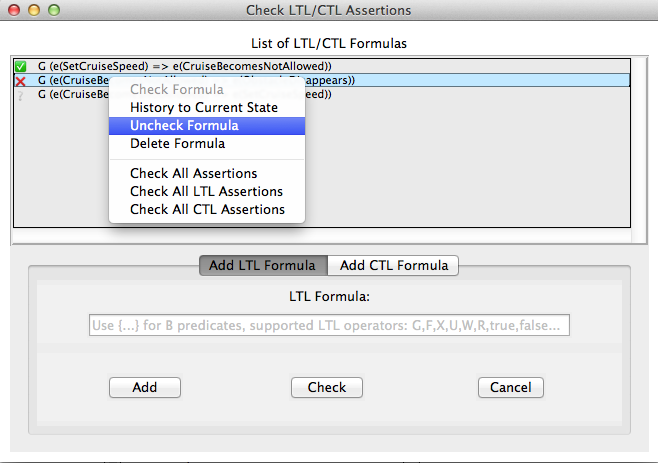
Additionally, the viewer provides a context menu for the list box elements. The context menu can be popped-up by a right-mouse-click on a formula from the list box, and it performs a set of actions available to be performed on the currently selected formula (see Figure below).
The old LTL and CTL dialogs can be accessed from "OldLtlViewers" in the menu bar.
LTL Preferences
There is a set of options coming with the LTL model checker. In this section we give a brief overview of the preferences. The LTL preferences can be viewed by selecting "LTL Preferences" in the "Preferences" menu of the LTL/CTL Assertions Viewer.
Exploring new states
The LTL model checker searches in the already explored search space of the model. If a state is encountered that has not been explored before, the state will be explored (i.e. all transitions to successor states are computed). The number of how often this can happen is limited by the field "Max no. of new states".
Depending on the LTL formula, a partially explored state space can be sufficient to find a counterexample or to assure the absence of a counterexample. If there's still the possibility of a counterexample in the remaining unexplored state space, the user will get a message.
Optimizing the process of LTL model checking
The process of model checking can be optimized for B and Event-B models by using partial order reduction. The idea of partial order reduction is to execute only a subset of all enabled actions in each state. Thus, only a part of the original state space is checked for the checked property. The reduction of the state space depends on the number of concurrent and independent actions in the model, as well as on the property being checked.
Search Options
The model checker searches for a counterexample (i.e. a path that does not satisfy the current formula). Where the checked paths through the model's search space start depend on the following options in the LTL Preferences’ menu:
- Start search in initialization
All paths that start in a state of the initialization of the machine are checked. - Start search in current state
All paths that start in the current state are checked. - Start in initialization, but check formula in current state
All paths that start in a state of the initialization of the machine are checked, but the formula is mapped to the current state. For example, this option can be used to check properties like "Is this state only reachable directly after executing operation `xy`?": The formula would be `Y[xy]`. This is equivalent to "G (current => f)" with f as the entered formula and using the option "Start search in initialization".
Note: Whereas `Y true` is always false when checked with option 1 or 2, it is usually true (but not in all cases) for option 3.
Supported Syntax
ProB supports LTL[e], an extended version of LTL. In contrast to the standard LTL, LTL[e] provides also support for propositions on transitions, not only on states. In practice, writing propositions on transitions is allowed by using the constructs `e(...)` and `[...]`. (see below). The LTL model checker of ProB supports Past-LTL[e] as well.
- Atomic propositions can be one of the following:
- Predicates can be written in curly braces: `{...}`. E.g. `{card(someset) > 1}`
- To check if an operation is enabled in a state use `e(Op)`, where `Op` is the name of the operation.
- To start a search from the current state of the animation use `current` (see the section LTL Preferences for more information).
- To check if a state has no outgoing transition leading to a different state use `sink`. This can be useful for finding "pseudo"-deadlocks, i.e. states where only query-operations are enabled that do not change the state. Note that `sink` holds for deadlock states as well.
- For checking if a state is a deadlock state the atomic proposition ` deadlock ` can be used.
- To check if a set of operations is disabled in a state use `deadlock(Op1,Op2,...,Opk)`, where Op1,Op2,...,Opk with k>0 are operations of the model. It is also possible to check if specific representations of an operation with arguments are disabled in a state using pattern-matching, e.g.: `deadlock(Op(1),Op(3))`.
- By means of `deterministic(Op1,Op2,...,Opk)`, where Op1,Op2,...,Opk with k>0 are operations of the model, one can check if maximum one of the operations Op1,Op2,...,Opk is enabled in a state.
- To check if exactly one operation from a set of operations Op1,Op2,...,Opk is enabled in a state use `controller(Op1,Op2,…,Opk)`.
- Transition propositions:
If the next executed operation in the path is `Op`, the expression `[Op]` can be used. Also patter-matching for the arguments of the operation is supported. E.g. `[Op(3,4*v)]` checks if the next operation is `Op` and that the first argument is 3 and the third argument is `4*v` where `v` is a variable of the machine.
Arbitrary B expressions can be used as patterns. Constants and variables of the machine can be used. Variables have the values of the state where the operations starts.
- Logical operators
- `true` and `false`
- `not`: negation
- &, `or` and =>: conjunction, disjunction and implication
- Temporal operators (future)
- `G f`: globally
- `F f`: finally
- `X f`: next
- `f U g`: until
- `f W g`: weak until
- `f R g`: release
- Temporal operators (past)
- `H f`: history (dual to G)
- `O f`: once (dual to F)
- `Y f`: yesterday (dual to X)
- `f S g`: since (dual to until)
- `f T g`: trigger (dual to release)
- Fairness operators
- `WF(Op)`: weak fairness, where ` Op` is an operation
- `SF(Op)`: strong fairness, where ` Op` is an operation
Setting Fairness Constraints
Fairness is a notion where the search for counterexamples is restricted to paths that do not ignore infinitely the execution of a set of enabled operations imposed by the user as "fair" constraints. One possibility to set fairness constraints in ProB is to encode them in the LTLe formula intended to be checked. For example, for a given LTLe formula "f" a set of weak fairness conditions {a1,…,an} can be given as follows:
(FG e(a1) => GF [a1]) & … & (FG e(an) => GF [an]) => f.
In a similar way, strong fairness constraints can be imposed expressed by means of an LTLe formula:
(GF e(a1) => GF [a1]) & … & (GF e(an) => GF [an]) => f.
Checking fairness in this way is very often considered to be inefficient as usually the number of atoms (the possible valuations of the property) of the LTL property is exponential in the size of the formula.[1] For this reason, the search algorithm of the LTL model checker has been extended in order to allow fairness to be checked efficiently. In addition, new operators have been added to the ProB’s LTL parser for setting fairness constraints to an LTLe property. The new operators are WF(-) and SF(-) and both accept as argument an operation. The fairness constraints must be given by means of implication: "fair => f", where "f" is the property to be checked and "fair" the fairness constraints.
In particular, "fair" can have one of the forms: "wfair", "sfair", "wfair & sfair", and "sfair & wfair", where "wfair" and "sfair" represent the imposed weak and strong fairness constraints, respectively.
Basically, "wfair" and "sfair" are expressed by means of logical formulas having the following syntax:
- Weak fair conditions ("wfair"):
- `WF(a)`, where `a` is an operation
- `&` and `or`: conjunction and disjunction
- Strong fair conditions ("sfair"):
- `SF(a)`, where `a` is an operation
- `&` and `or`: conjunction and disjunction
For instance, if we want to check an LTL property "f" on paths that are weak fair in regard to the operations "a" and "b" and additionally strong fair in regard to "c" or "d", then this can be given as follows:
(WF(a) & WF(b)) & (SF(c) or SF(d)) => f
Note that the operators WF(-) and SF(-) cannot appear on the right side of the fairness implication. Basically, WF(-) and SF(-) can be described by the following equivalences:
WF(a) ≡ (FG e(a) => GF [a]) and SF(a) ≡ (GF e(a) => GF [a]), where a is an operation.
Storing LTL Assertions in the Model
Storing LTL formulas in B machines
LTL formulas can be stored in the `DEFINITIONS` section of a B machine. The name of the definition must start with `ASSERT_LTL` and a string must be specified. In case there is more than one LTL assertion given in the ‘DEFINITIONS’ section, the particular LTL assertions must be separated by semicolon. For example:
DEFINITIONS ASSERT_LTL == "G (e(SetCruiseSpeed) => e(CruiseBecomesNotAllowed))"; ASSERT_LTL1 == "G (e(CruiseBecomesNotAllowed) => e(SetCruiseSpeed))"; ASSERT_LTL2 == "G (e(CruiseBecomesNotAllowed) => (ObstacleDisappears))"
Storing LTL formulas in CSP-M specifications
LTL formulas can be stored within pragmas in CSP-M specifications. A pragma in which a single LTL formula is stored has the form "{-# assert_ltl "f" "c" #-}", where "assert_ltl" indicates the type of the information stored in the pragma (there are currently two types: assert_ltl and assert_ctl), and is followed by the LTL formula f and a comment (the comment is optional). Both, the LTL formula and the comment, must be enclosed in double quotes.
It is also possible to give several LTL formulas in a single pragma within which the particular LTL assertions are separated by semicolon. For example:
{-# assert_ltl "SF(enter.1) & WF(req.1) => GF([enter.1])";
assert_ltl "SF(enter.2) & WF(req.2) => GF([enter.2])";
assert_ltl "GF [enter.1] & GF [enter.2]" "Should fail."#-}
Note that a semicolon must not follow the last assertion in a pragma.
LTL formulas in a separate file
With the command line version of ProB it is possible to check several LTL formulas with one call. The command has the following syntax
probcli -ltlfile FILE ...
The file FILE contains one or more sections where each section has the form
[Name] Formula
The formula itself can spread several lines. Additional comments can be added with a leading #. If a counter-example is found, the trace of the counter-example is saved into the file ltlce_Name.trace, where "Name" is the name of the formula in the LTL file.
References
- ↑ O. Lichtenstein and A. Pnueli: Checking that Finite State Concurrent Programs Satisfy Their Linear Specification. POPL '85, Proceedings of the 12th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, ACM, 1985