LTL Model Checking: Difference between revisions
No edit summary |
Jan Gruteser (talk | contribs) mNo edit summary |
||
| (50 intermediate revisions by 5 users not shown) | |||
| Line 6: | Line 6: | ||
[[File:ltlviewer.png]] | [[File:ltlviewer.png]] | ||
All LTL formulas that are given in the " | All LTL formulas that are given in the "DEFINITIONS" section of a B machine are displayed in the list box of the LTL/CTL Assertions Viewer. For CSP-M specifications all LTL formulas given in the LTL pragmas of the loaded CSP-M file will be shown in the viewer. (For more detailed information of how LTL/CTL assertions can be stored into B and CSP-M models see Section '''Storing LTL Assertions into a Model'''). | ||
A new LTL formula can be entered in the entry below the list box. (We explain the supported syntax below). The typed formula can then be either added to the list box by clicking the "Add" button or directly checked by clicking the "Check" button. Before doing that assure whether you are in the proper frame ("Add LTL Formula") of the bottom part of the LTL viewer. | A new LTL formula can be entered in the entry below the list box. (We explain the supported syntax below). The typed formula can then be either added to the list box by clicking the "Add" button or directly checked by clicking the "Check" button. Before doing that assure whether you are in the proper frame ("Add LTL Formula") of the bottom part of the LTL viewer. | ||
The LTL model checker can be started for an LTL formula by performing a double-click on the respective formula or typing "Enter" after selecting the respective formula. Each LTL formula in the list box has on the left hand side a symbol that indicates what the status of the respective formula | The LTL model checker can be started for an LTL formula by performing a double-click on the respective formula or typing "Enter" after selecting the respective formula. Each LTL formula in the list box has on the left hand side a symbol that indicates what is the status of the respective formula. An LTL formula can have one of the following statuses (status symbols may differ under different operating systems): | ||
* ? – The formula has not been checked yet. | * ? – The formula has not been checked yet. | ||
| Line 37: | Line 37: | ||
'''Optimizing the process of LTL model checking'''<br/> | '''Optimizing the process of LTL model checking'''<br/> | ||
The process of model checking can be optimized for B and Event-B models by using partial order reduction. The idea of partial order reduction is to execute only a subset of all enabled actions in each state. Thus, only a part of the original state space is checked for the checked property. The reduction of the state space depends on the number of concurrent and independent actions in the model, as well as on the property being checked. | The process of model checking can be optimized for B and Event-B models by using partial order reduction. The idea of partial order reduction is to execute only a subset of all enabled actions in each state. Thus, only a part of the original state space is checked for the checked property. The reduction of the state space depends on the number of concurrent and independent actions in the model, as well as on the property being checked. | ||
'''With Safety Check'''<br/> | |||
This checks whether a formula is a safety property or not. | |||
If it is, this property is treated in an optimised way. | |||
In some cases, this means that not the entire state space has to be computed. | |||
For this optimisation to work, ProB needs the LTL2BA translator. | |||
You can download and put it into ProB's lib folder, by choosing | |||
Download and Install LTL2BA Tool | |||
from the Help menu. | |||
More details can be found below. | |||
'''Search Options'''<br/> | '''Search Options'''<br/> | ||
| Line 47: | Line 58: | ||
=== Supported Syntax === | === Supported Syntax === | ||
ProB supports LTL<sup>e</sup>, an extended version of LTL. In contrast to standard LTL, LTL<sup>e</sup> also | ProB supports LTL<sup>[e]</sup>, an extended version of LTL. In contrast to the standard LTL, LTL<sup>[e]</sup> provides also support for propositions on transitions, not only on states. In practice, writing propositions on transitions is allowed by using the constructs `e(...)` and `[...]`. (see below). The LTL model checker of ProB supports Past-LTL<sup>[e]</sup> as well. | ||
* Atomic propositions can be one of the following: | * Atomic propositions can be one of the following: | ||
** | ** Predicates can be written in curly braces: `{...}`. E.g. `{card(someset) > 1}` | ||
** To check if an operation is enabled in a state | ** To check if an operation is enabled in a state use `e(Op)`, where `Op` is the name of the operation. | ||
** | ** To start a search from the current state of the animation use `current` (see the section '''LTL Preferences''' for more information). | ||
** | ** To check if a state has no outgoing transition leading to a different state use `sink`. This can be useful for finding "pseudo"-deadlocks, i.e. states where only query-operations are enabled that do not change the state. Note that `sink` holds for deadlock states as well. | ||
** | ** For checking if a state is a deadlock state the atomic proposition ` deadlock ` can be used. | ||
** To check if a set of operations is disabled in a state use `deadlock(Op1,Op2,...,Opk)`, where Op1,Op2,...,Opk with k>0 are operations of the model. It is also possible to check if specific representations of an operation with arguments are disabled in a state using pattern-matching, e.g.: `deadlock(Op(1),Op(3))`. | |||
** By means of `deterministic(Op1,Op2,...,Opk)`, where Op1,Op2,...,Opk with k>0 are operations of the model, one can check if maximum one of the operations Op1,Op2,...,Opk is enabled in a state. | |||
** To check if exactly one operation from a set of operations Op1,Op2,...,Opk is enabled in a state use `controller(Op1,Op2,…,Opk)`. | |||
* Transition propositions: | * Transition propositions: | ||
** If the next executed operation in the path is `Op`, the expression `[Op]` can be used. Also patter-matching for the arguments of the operation is supported. E.g. `[Op(3,4*v)]` checks if the next operation is `Op` and that the first argument is 3 and the third argument is `4*v` where `v` is a variable of the machine. <br> Arbitrary B expressions can be used as patterns. Constants and variables of the machine can be used. Variables have the values of the state where the operations starts. | |||
** The following are now also available in ProB 1.12: | |||
*** `unchanged({BExpr})` check if the B expression BExpr is unchanged compared to the next state | |||
*** `changed({BExpr}) ` check if the BExpr is changed by the next transition | |||
*** `decreasing({BExpr})` check if the BExpr will decrease due to the next transition | |||
***` increasing({BExpr}) ` check if the BExpr will increase due to the next transition | |||
*** ` BA({BPred}) ` check before-after B predicate BPred on current and next state, where x$0 refers to value in current (before) state, and x to value in next (after) state | |||
* Logical operators | * Logical operators | ||
** `true` and `false` | ** `true` and `false` | ||
** `not`: negation | ** `not`: negation | ||
** &, `or` and =>: conjunction, disjunction and implication | ** `&`, `or` and `=>`: conjunction, disjunction and implication | ||
* Temporal operators (future) | * Temporal operators (future) | ||
| Line 80: | Line 100: | ||
* Fairness operators | * Fairness operators | ||
** `WF(Op)`: weak fairness, where ` Op` is an operation | ** `WF(Op)` or `wf(Op)`: weak fairness, where ` Op` is an operation | ||
** `SF(Op)`: strong fairness, where ` Op` is an operation | ** `SF(Op)`or `sf(Op)`: strong fairness, where ` Op` is an operation | ||
** `WEF`: weak fairness for all possible operations | |||
** `SEF`: strong fairness for all possible operations | |||
==Safety Properties == | |||
For safety properties ProB uses another checking algorithm, to avoid having to explore the entire SCC (strongly connected component) of a counter example. | |||
In general this requires installing the LTL2BA tool (see Help menu), but the following patterns are supported directly without LTL2BA: | |||
G StateProposition | |||
G (StateProposition => X StateProposition) | |||
where StateProposition is either an atomic proposition ({Pred}, e(Op), [Op], deadlock,...) or a propositional operators (not, &, =>, or) applied to StatePropositions. | |||
Here are a few example patterns covered by the above: | |||
G {Pred} Invariant | |||
G(e(Op) => {Pred}) Necessary precondition for operation Op | |||
G({Pred} => e(Op)) Sufficient precondition for operation Op | |||
G([Op] => X{Pred}) Postcondition of operation Op | |||
G(e(Op1) => not(e(Op2))) Enabling relations between operations | |||
G(not(deadlock(Op1,...,Opk))) Relative deadlock freedom | |||
G(deterministic(Op1,...,Opk)) Relative deadlock freedom | |||
G(controller(Op1,...,Opk)) Relative deadlock freedom and determinism | |||
==Setting Fairness Constraints== | ==Setting Fairness Constraints== | ||
Fairness is a notion where the search for counterexamples is restricted to paths that do not ignore infinitely the execution of a set of enabled operations imposed by the user as "fair" constraints. One possibility to set fairness constraints in ProB is to encode them in the LTL<sup>e</sup> formula intended to be checked. For example, for a given LTL<sup>e</sup> formula "f" a set of weak fairness conditions {a1,…,an} can be given as follows: | Fairness is a notion where the search for counterexamples is restricted to paths that do not ignore infinitely the execution of a set of enabled operations imposed by the user as "fair" constraints. One possibility to set fairness constraints in ProB is to encode them in the LTL<sup>[e]</sup> formula intended to be checked. For example, for a given LTL<sup>[e]</sup> formula "f" a set of weak fairness conditions {a1,…,an} can be given as follows: | ||
(FG e(a1) => GF [a1]) & … & (FG e(an) => GF [an]) => f. | (FG e(a1) => GF [a1]) & … & (FG e(an) => GF [an]) => f. | ||
In a similar way, strong fairness constraints can be imposed expressed by means of an LTL<sup>e</sup> formula: | In a similar way, strong fairness constraints can be imposed expressed by means of an LTL<sup>[e]</sup> formula: | ||
(GF e(a1) => GF [a1]) & … & (GF e(an) => GF [an]) => f. | (GF e(a1) => GF [a1]) & … & (GF e(an) => GF [an]) => f. | ||
Checking fairness in this way is very often considered to be inefficient as the | Checking fairness in this way is very often considered to be inefficient as usually the number of atoms (the possible valuations of the property) of the LTL property is exponential in the size of the formula.<ref>O. Lichtenstein and A. Pnueli: ''Checking that Finite State Concurrent Programs Satisfy Their Linear Specification''. POPL '85, Proceedings of the 12th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, ACM, 1985</ref> For this reason, the search algorithm of the LTL model checker has been extended in order to allow fairness to be checked efficiently. In addition, new operators have been added to the ProB’s LTL parser for setting fairness constraints to an LTL<sup>[e]</sup> property. The new operators are ''WF(-)'' and ''SF(-)'' and both accept as argument an operation. The fairness constraints must be given by means of implication: "fair => f", where "f" is the property to be checked and "fair" the fairness constraints. | ||
In particular, "fair" can have one of the forms: "wfair", "sfair", "wfair & sfair", and "sfair & wfair", where "wfair" and "sfair" represent the imposed weak and strong fairness constraints, respectively. | In particular, "fair" can have one of the forms: "wfair", "sfair", "wfair & sfair", and "sfair & wfair", where "wfair" and "sfair" represent the imposed weak and strong fairness constraints, respectively. | ||
| Line 107: | Line 148: | ||
(WF(a) & WF(b)) & (SF(c) or SF(d)) => f | (WF(a) & WF(b)) & (SF(c) or SF(d)) => f | ||
Note that the operators ''WF(-)'' and ''SF(-)'' cannot | Note that the operators ''WF(-)'' and ''SF(-)'' cannot appear on the right side of the fairness implication. Basically, ''WF(-)'' and ''SF(-)'' can be described by the following equivalences: | ||
WF(a) ≡ (FG e(a) => GF [a]) and SF(a) ≡ (GF e(a) => GF [a]), where a is an operation. | WF(a) ≡ (FG e(a) => GF [a]) and SF(a) ≡ (GF e(a) => GF [a]), where a is an operation. | ||
For setting fairness constraints on all possible operations of the model being checked use the operators "WEF" and "SEF". For instance, if "f" is a liveness property and we want to restrict the search only to strongly fair paths, then we can impose the fairness constraints by means of the formula "SEF => f". | |||
The grammar for imposing fairness constraints by means of the fairness implication ("fair => f") looks as follows: | |||
fair ::= WEF | SEF | wfair | sfair | wfair & sfair | sfair & wfair<br/> | |||
wfair ::= wf(a) | ( wfair ) | wfair & wfair | wfair or wfair<br/> | |||
sfair ::= sf(a) | ( sfair ) | sfair & sfair | sfair or sfair | |||
where "a" is a transition proposition. | |||
==Storing LTL Assertions in the Model== | ==Storing LTL Assertions in the Model== | ||
| Line 121: | Line 172: | ||
'''Storing LTL formulas in CSP-M specifications'''<br/> | '''Storing LTL formulas in CSP-M specifications'''<br/> | ||
LTL formulas can be stored within pragmas in CSP-M specifications. A pragma in which a single LTL formula is stored | LTL formulas can be stored within pragmas in CSP-M specifications. A pragma in which a single LTL formula is stored is given by "{-# assert_ltl "f" "c" #-}", where "assert_ltl" indicates the type of the information stored in the pragma (there are currently two types: assert_ltl and assert_ctl), and is followed by the LTL formula `f` and a comment `c` (the comment is optional). Both, the LTL formula and the comment, must be enclosed in double quotes. | ||
It is also possible to give several LTL formulas in a single pragma within which the | It is also possible to give several LTL formulas in a single pragma within which the corresponding LTL assertions are separated by semicolon. For example: | ||
{-# assert_ltl "SF(enter.1) & WF(req.1) => GF([enter.1])"; | {-# assert_ltl "SF(enter.1) & WF(req.1) => GF([enter.1])"; | ||
| Line 128: | Line 179: | ||
assert_ltl "GF [enter.1] & GF [enter.2]" "Should fail."#-} | assert_ltl "GF [enter.1] & GF [enter.2]" "Should fail."#-} | ||
Note that a semicolon must not follow the last | Note that a semicolon must not follow the last assertion in a pragma. | ||
For CSP-M specifications, it is also possible to assert LTL-formulae to particular processes in the model. This is possible by means of ``assert`` declarations, which have been recently included to the CSP-M grammar of the ProB CSP-M parser: | |||
With the command line version of ProB it is possible to check several LTL | assert P |= LTL: "ltl-formula", | ||
where `P` is an arbitrary process and `ltl-formula` an LTL formula. | |||
==LTL Formulas in a Separate File== | |||
With the command line version of ProB it is possible to check several LTL<sup>[e]</sup> formulae with one call. The command has the following syntax | |||
probcli -ltlfile FILE ... | probcli -ltlfile FILE ... | ||
The file FILE contains one or more sections where each section has the form | The file FILE contains one or more sections where each section has the form | ||
| Line 138: | Line 194: | ||
The formula itself can spread several lines. Additional comments can be added with a leading #. | The formula itself can spread several lines. Additional comments can be added with a leading #. | ||
If a counter-example is found, the trace of the counter-example is saved into the file ltlce_Name.trace, where "Name" is the name of the formula in the LTL file. | If a counter-example is found, the trace of the counter-example is saved into the file ltlce_Name.trace, where "Name" is the name of the formula in the LTL file. | ||
One also can check a single LTL<sup>[e]</sup> formula ''F'' using the option '-ltlformula' as follows: | |||
probcli -ltlformula "F" ... | |||
==LTL Formulae in a Separate File== | |||
With the command line version of ProB it is possible to check several LTL<sup>[e]</sup> formulae with one call. The command has the following syntax | |||
probcli -ltlfile FILE ... | |||
The file FILE contains one or more sections where each section has the form | |||
[Name] Formula | |||
The formula itself can spread in several lines. Additional comments can be added with a leading #. | |||
If a counter-example is found, the trace of the counter-example is saved into the file ltlce_Name.trace, where "Name" is the name of the formula in the LTL file. | |||
One also can check a single LTL<sup>[e]</sup> formula ''F'' using the option '-ltlformula' as follows: | |||
probcli -ltlformula "F" ... | |||
==LTL Model Checker Output== | |||
The output provided by the LTL model checker can sometimes reveal some interesting statistical facts about the model and the property being checked on the model. The LTL model checker of ProB uses the tableau approach for checking an LTL<sup>[e]</sup> formula on a formal model. To check whether a model ''M'' satisfies a given formula ''f'', the algorithm generates a search graph, called also tableau graph, composed from the tableau of the formula and the state space of the model. If there is a path in the search graph that is a model for ''f'', then the formula is satisfiable. The nodes of the search graph are called ''atoms''. | |||
Basically, using the tableau approach we prove that ''M'' satisfies ''f'' by negating the given formula and searching for a path fulfilling ''¬f''. If such a path is found, then we infer that ''M'' violates ''f''. Otherwise, if no path is found that satisfies ''¬f'', we conclude that ''M |= f''. The LTL model checking algorithm of ProB is based on searching for strongly connected components (SCCs) with certain properties to determine whether ''M'' satisfies ''f''. Finding such an SCC that can be reached from an initial state of ''M'' is a witness for a counter-example for ''f''. Sometimes, we use fairness to ignore such SCCs that do not fulfill the imposed fairness constraints in order to not impede proving a property by returning of non-fair paths as counter-examples. | |||
The LTL model checker algorithm of ProB is implemented in C using a callback mechanism for evaluating the atomic propositions and the outgoing transitions in SICStus Prolog. (For each state of the model a callback will be performed.) Additionally, the search for SCCs is based on the Tarjan's algorithm. In the terminal all messages coming from the LTL model checker are preceded either by "LTL (current statistics): " or "LTL model checking:". The output from the LTL model checker can give helpful insights about the model and the model checking process. | |||
Consider the CSP specifications "dphil_ltl8.csp" representing a model of the dining philosophers problem for eight philosophers which resolves the starvation problem by always forcing the first philosopher to pick up first the right fork instead of the left one. In other words, "dphil_ltl8.csp" has no deadlock states. Checking the LTL formula "GF [eat.0]" from the command line will produce the following output: | |||
<pre> | |||
$ probcli -ltlformula "GF [eat.0]" dphil_ltl8.csp | |||
.... | |||
LTL model checking formula | |||
% parsing_ltl_formula | |||
% initialising_ltlc | |||
starting_model_checking | |||
LTL (current statistics): 13280 atoms, 10070 transitions generated, and 2631 callbacks needed. | |||
LTL model checking: found counter-example (lasso-form): intro length = 1126, path in SCC of length = 5 | |||
LTL model checking: memory usage approx. 1924 KiB, 14104 atoms and 10724 transitions generated | |||
LTL model checking: total time 22492ms, 2803 callbacks needed 22465ms, netto 26ms. | |||
! An error occurred ! | |||
! source(ltl) | |||
! Model Check Counter-Example found for: | |||
! GF [eat.0] | |||
Formula FALSE. | |||
Runtime: 22220 ms | |||
! *** error occurred *** | |||
! ltl | |||
</pre> | |||
As one can clearly see from the output, the LTL model checker fails to prove "GF [eat.0]" on the model since it has found a counter-example for the formula. Note that the ProB LTL model checker explores the search graph and the state space dynamically. The above data is to be understand as follows: | |||
* 14104 atoms - the LTL model checker needed to explore 14104 atoms to find a counter-example for the formula. | |||
* 2803 callbacks needed - to explore the search graph the model checker makes callbacks in order to explore the state space of the model being checked (the exploration runs dynamically) and compute the successor states in the tableau graph. In this case the model checker has needed to explore 2803 states till it finds a counter-example for the formula | |||
* memory usage approx. 1924 KiB - the memory needed to explore the tableau graph | |||
* found counter-example (lasso-form) - means that the counter-example being found is path beginning in an initial state of the model and reaching a state that closes a cycle: | |||
** intro length = 1126: the length of the sub-path from an initial state to the entry point of the cycle | |||
** path in SCC of length = 5: the cycle is comprised of five states | |||
* total time 22492ms - the LTL model checker needed about 23 seconds to find the counter-example. Here a distinction between the time needed to explore the state space of the model (2803 callbacks needed 22465ms) and the time spent for generating the tableau graph + the time for identifying the self-fulfilling SCC (netto 26ms) | |||
* LTL (current statistics) - an intermediate data information is given each 20 seconds spent from the last current data information. | |||
In the example above one can prove the LTL<sup>[e]</sup> formula "GF [eat.0]" on dphil_ltl6.csp using fairness. One can impose, for example, strong fairness conditions on all transitions of the model and thus verify that "GF [eat.0]" is satisfied under strong fairness. The call looks as follows: | |||
<pre> | |||
$ probcli -ltlformula "SEF => GF [eat.0]" dphil_ltl8.csp | |||
... | |||
LTL model checking formula | |||
% parsing_ltl_formula | |||
% initialising_ltlc | |||
starting_model_checking | |||
LTL (current statistics): 13016 atoms, 9834 transitions generated, and 2578 callbacks needed. | |||
LTL (fairness): 0 strongly connected components were rejected, 0 callbacks needed. | |||
LTL (current statistics): 27540 atoms, 44422 transitions generated, and 5123 callbacks needed. | |||
LTL (fairness): 284 strongly connected components were rejected, 843 callbacks needed. | |||
..... | |||
LTL (current statistics): 85980 atoms, 267821 transitions generated, and 19733 callbacks needed. | |||
LTL (fairness): 454 strongly connected components were rejected, 1924 callbacks needed. | |||
LTL (current statistics): 95648 atoms, 364288 transitions generated, and 22150 callbacks needed. | |||
LTL (fairness): 773 strongly connected components were rejected, 3085 callbacks needed. | |||
LTL model checking: memory usage approx. 13829 KiB, 96500 atoms and 381625 transitions generated | |||
LTL model checking: total time 190887ms, 22363 callbacks needed 186690ms, netto 467ms. | |||
LTL model checking (fairness): 800 strongly connected components were rejected. | |||
LTL model checking (fairness): total fairness checking time 3729ms, 3246 callbacks needed 3452ms, netto 277ms. | |||
LTL Formula TRUE. | |||
No counter example found for SEF => GF [eat.0]. | |||
Runtime: 188370 ms | |||
</pre> | |||
In the above check no fair counter-example could be found for the formula "GF [eat.0]". For this check the search graph comprises 96500 atoms and 381625 transitions, far more than the previous formula check (without fairness assumptions). Since no fair counter-example was found we can infer that the whole state space of the model was explored. Further, since we know from above that 22363 callbacks were needed to explore the search graph, we can infer that the state space of the model has in total 22363 states. | |||
In the output above there is also some information about the fairness checking being performed for the model checker run. Form the fairness statistics we can see that the model checker has refuted 800 SCCs in total, i.e. there were 800 SCCs in the search graph that could serve as a counter-example for "GF [eat.0]" in case no fairness constraints were imposed. | |||
== Other Relevant Tutorials about LTL Model Checking == | |||
A brief tutorial on visualizing LTL counter-examples in the Rodin tool can be found [[Tutorial LTL Counter-example View|here]]. | |||
A tutorial of a simple case study, where setting fairness constraints to some of the LTL properties is required, can be found [[Mutual Exclusion (Fairness)|here] | |||
== Summary of CTL Syntax supported by ProB == | |||
CTL formulas f can be constructed from: | |||
- atomic propositions: | |||
{ Pred } to check if a B predicate Pred holds in the current state, e.g. {card(someset) > 1} | |||
e(op) to check if an operation op is enabled | |||
- propositional logic operators: | |||
not f | |||
f or g | |||
f & g | |||
f => g | |||
- temporal operators: | |||
EX f there is a next state satisfying f | |||
EX[Op] f there is a next state via Op satisfying f, e.g. EX[reset]{db={}} | |||
AX f all next states satisfy f | |||
EF f there exists a path where f holds in the future | |||
EG f there exists a path where f holds globally | |||
AF f for all paths f holds in the future | |||
AG f for all paths f holds globally | |||
E f U g there exists a path where f holds until g | |||
Note: a model satisfies a CTL formula iff the formula holds in all initial states. | |||
== References == | |||
<references /> | |||
Latest revision as of 16:10, 13 June 2025
ProB provides support for LTL (linear temporal logic) model checking. For an introduction to LTL see the Wikipedia Article.
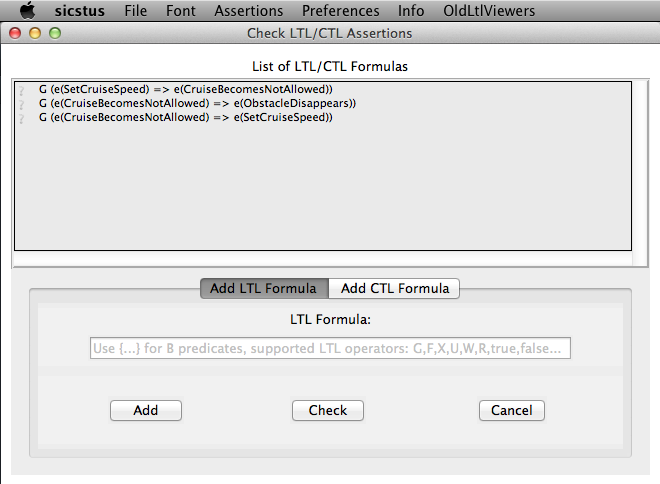
To use this feature, select "Check LTL/CTL Assertions" in the "Verify" menu. The feature can also be accessed by the key combination "Ctrl+L" under Windows and Linux, and by the key combination "Cmd+L" under MacOS. The following window appears:
All LTL formulas that are given in the "DEFINITIONS" section of a B machine are displayed in the list box of the LTL/CTL Assertions Viewer. For CSP-M specifications all LTL formulas given in the LTL pragmas of the loaded CSP-M file will be shown in the viewer. (For more detailed information of how LTL/CTL assertions can be stored into B and CSP-M models see Section Storing LTL Assertions into a Model).
A new LTL formula can be entered in the entry below the list box. (We explain the supported syntax below). The typed formula can then be either added to the list box by clicking the "Add" button or directly checked by clicking the "Check" button. Before doing that assure whether you are in the proper frame ("Add LTL Formula") of the bottom part of the LTL viewer.
The LTL model checker can be started for an LTL formula by performing a double-click on the respective formula or typing "Enter" after selecting the respective formula. Each LTL formula in the list box has on the left hand side a symbol that indicates what is the status of the respective formula. An LTL formula can have one of the following statuses (status symbols may differ under different operating systems):
- ? – The formula has not been checked yet.
- ✔ – The formula is true for all valid paths.
- ✘ – A counterexample for the formula has been found, i.e. there is a path that violates the formula. In case the formula has been just checked on the model the animator is navigated to the last state of the counterexample. The full path can then be seen in the history. The counterexample can be also obtained by the dotty-viewer after a second double-click on the formula in the assertions’ viewer.
- ⌚ – The formula is currently checked.
- ! – The formula check has been aborted by an unexpected error occurrence.
- ∞ – The formula check is incomplete, i.e. no counterexample was found so far, but the absence of a path that does not satisfy the formula can not be guaranteed because the state space was not fully explored. A new check can be started by a double-click.
All formulas can be checked by "Assertions -> Check All Assertions" in the menu bar. All formulas will be then checked from top to bottom in the list box.
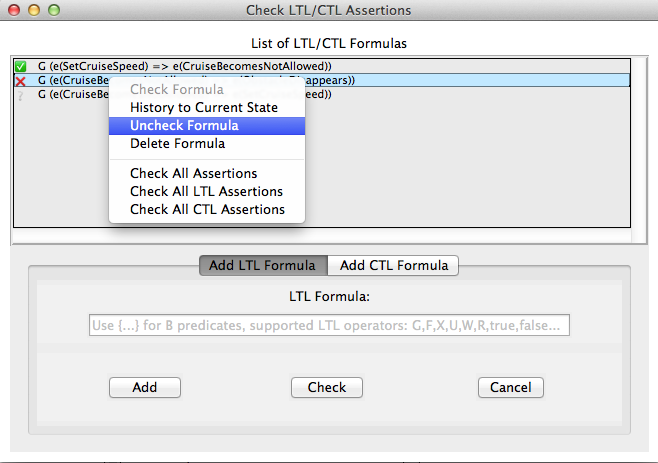
Additionally, the viewer provides a context menu for the list box elements. The context menu can be popped-up by a right-mouse-click on a formula from the list box, and it performs a set of actions available to be performed on the currently selected formula (see Figure below).
The old LTL and CTL dialogs can be accessed from "OldLtlViewers" in the menu bar.
LTL Preferences
There is a set of options coming with the LTL model checker. In this section we give a brief overview of the preferences. The LTL preferences can be viewed by selecting "LTL Preferences" in the "Preferences" menu of the LTL/CTL Assertions Viewer.
Exploring new states
The LTL model checker searches in the already explored search space of the model. If a state is encountered that has not been explored before, the state will be explored (i.e. all transitions to successor states are computed). The number of how often this can happen is limited by the field "Max no. of new states".
Depending on the LTL formula, a partially explored state space can be sufficient to find a counterexample or to assure the absence of a counterexample. If there's still the possibility of a counterexample in the remaining unexplored state space, the user will get a message.
Optimizing the process of LTL model checking
The process of model checking can be optimized for B and Event-B models by using partial order reduction. The idea of partial order reduction is to execute only a subset of all enabled actions in each state. Thus, only a part of the original state space is checked for the checked property. The reduction of the state space depends on the number of concurrent and independent actions in the model, as well as on the property being checked.
With Safety Check
This checks whether a formula is a safety property or not.
If it is, this property is treated in an optimised way.
In some cases, this means that not the entire state space has to be computed.
For this optimisation to work, ProB needs the LTL2BA translator.
You can download and put it into ProB's lib folder, by choosing
Download and Install LTL2BA Tool
from the Help menu. More details can be found below.
Search Options
The model checker searches for a counterexample (i.e. a path that does not satisfy the current formula). Where the checked paths through the model's search space start depend on the following options in the LTL Preferences’ menu:
- Start search in initialization
All paths that start in a state of the initialization of the machine are checked. - Start search in current state
All paths that start in the current state are checked. - Start in initialization, but check formula in current state
All paths that start in a state of the initialization of the machine are checked, but the formula is mapped to the current state. For example, this option can be used to check properties like "Is this state only reachable directly after executing operation `xy`?": The formula would be `Y[xy]`. This is equivalent to "G (current => f)" with f as the entered formula and using the option "Start search in initialization".
Note: Whereas `Y true` is always false when checked with option 1 or 2, it is usually true (but not in all cases) for option 3.
Supported Syntax
ProB supports LTL[e], an extended version of LTL. In contrast to the standard LTL, LTL[e] provides also support for propositions on transitions, not only on states. In practice, writing propositions on transitions is allowed by using the constructs `e(...)` and `[...]`. (see below). The LTL model checker of ProB supports Past-LTL[e] as well.
- Atomic propositions can be one of the following:
- Predicates can be written in curly braces: `{...}`. E.g. `{card(someset) > 1}`
- To check if an operation is enabled in a state use `e(Op)`, where `Op` is the name of the operation.
- To start a search from the current state of the animation use `current` (see the section LTL Preferences for more information).
- To check if a state has no outgoing transition leading to a different state use `sink`. This can be useful for finding "pseudo"-deadlocks, i.e. states where only query-operations are enabled that do not change the state. Note that `sink` holds for deadlock states as well.
- For checking if a state is a deadlock state the atomic proposition ` deadlock ` can be used.
- To check if a set of operations is disabled in a state use `deadlock(Op1,Op2,...,Opk)`, where Op1,Op2,...,Opk with k>0 are operations of the model. It is also possible to check if specific representations of an operation with arguments are disabled in a state using pattern-matching, e.g.: `deadlock(Op(1),Op(3))`.
- By means of `deterministic(Op1,Op2,...,Opk)`, where Op1,Op2,...,Opk with k>0 are operations of the model, one can check if maximum one of the operations Op1,Op2,...,Opk is enabled in a state.
- To check if exactly one operation from a set of operations Op1,Op2,...,Opk is enabled in a state use `controller(Op1,Op2,…,Opk)`.
- Transition propositions:
- If the next executed operation in the path is `Op`, the expression `[Op]` can be used. Also patter-matching for the arguments of the operation is supported. E.g. `[Op(3,4*v)]` checks if the next operation is `Op` and that the first argument is 3 and the third argument is `4*v` where `v` is a variable of the machine.
Arbitrary B expressions can be used as patterns. Constants and variables of the machine can be used. Variables have the values of the state where the operations starts. - The following are now also available in ProB 1.12:
- `unchanged({BExpr})` check if the B expression BExpr is unchanged compared to the next state
- `changed({BExpr}) ` check if the BExpr is changed by the next transition
- `decreasing({BExpr})` check if the BExpr will decrease due to the next transition
- ` increasing({BExpr}) ` check if the BExpr will increase due to the next transition
- ` BA({BPred}) ` check before-after B predicate BPred on current and next state, where x$0 refers to value in current (before) state, and x to value in next (after) state
- If the next executed operation in the path is `Op`, the expression `[Op]` can be used. Also patter-matching for the arguments of the operation is supported. E.g. `[Op(3,4*v)]` checks if the next operation is `Op` and that the first argument is 3 and the third argument is `4*v` where `v` is a variable of the machine.
- Logical operators
- `true` and `false`
- `not`: negation
- `&`, `or` and `=>`: conjunction, disjunction and implication
- Temporal operators (future)
- `G f`: globally
- `F f`: finally
- `X f`: next
- `f U g`: until
- `f W g`: weak until
- `f R g`: release
- Temporal operators (past)
- `H f`: history (dual to G)
- `O f`: once (dual to F)
- `Y f`: yesterday (dual to X)
- `f S g`: since (dual to until)
- `f T g`: trigger (dual to release)
- Fairness operators
- `WF(Op)` or `wf(Op)`: weak fairness, where ` Op` is an operation
- `SF(Op)`or `sf(Op)`: strong fairness, where ` Op` is an operation
- `WEF`: weak fairness for all possible operations
- `SEF`: strong fairness for all possible operations
Safety Properties
For safety properties ProB uses another checking algorithm, to avoid having to explore the entire SCC (strongly connected component) of a counter example. In general this requires installing the LTL2BA tool (see Help menu), but the following patterns are supported directly without LTL2BA:
G StateProposition G (StateProposition => X StateProposition)
where StateProposition is either an atomic proposition ({Pred}, e(Op), [Op], deadlock,...) or a propositional operators (not, &, =>, or) applied to StatePropositions.
Here are a few example patterns covered by the above:
G {Pred} Invariant
G(e(Op) => {Pred}) Necessary precondition for operation Op
G({Pred} => e(Op)) Sufficient precondition for operation Op
G([Op] => X{Pred}) Postcondition of operation Op
G(e(Op1) => not(e(Op2))) Enabling relations between operations
G(not(deadlock(Op1,...,Opk))) Relative deadlock freedom
G(deterministic(Op1,...,Opk)) Relative deadlock freedom
G(controller(Op1,...,Opk)) Relative deadlock freedom and determinism
Setting Fairness Constraints
Fairness is a notion where the search for counterexamples is restricted to paths that do not ignore infinitely the execution of a set of enabled operations imposed by the user as "fair" constraints. One possibility to set fairness constraints in ProB is to encode them in the LTL[e] formula intended to be checked. For example, for a given LTL[e] formula "f" a set of weak fairness conditions {a1,…,an} can be given as follows:
(FG e(a1) => GF [a1]) & … & (FG e(an) => GF [an]) => f.
In a similar way, strong fairness constraints can be imposed expressed by means of an LTL[e] formula:
(GF e(a1) => GF [a1]) & … & (GF e(an) => GF [an]) => f.
Checking fairness in this way is very often considered to be inefficient as usually the number of atoms (the possible valuations of the property) of the LTL property is exponential in the size of the formula.[1] For this reason, the search algorithm of the LTL model checker has been extended in order to allow fairness to be checked efficiently. In addition, new operators have been added to the ProB’s LTL parser for setting fairness constraints to an LTL[e] property. The new operators are WF(-) and SF(-) and both accept as argument an operation. The fairness constraints must be given by means of implication: "fair => f", where "f" is the property to be checked and "fair" the fairness constraints.
In particular, "fair" can have one of the forms: "wfair", "sfair", "wfair & sfair", and "sfair & wfair", where "wfair" and "sfair" represent the imposed weak and strong fairness constraints, respectively.
Basically, "wfair" and "sfair" are expressed by means of logical formulas having the following syntax:
- Weak fair conditions ("wfair"):
- `WF(a)`, where `a` is an operation
- `&` and `or`: conjunction and disjunction
- Strong fair conditions ("sfair"):
- `SF(a)`, where `a` is an operation
- `&` and `or`: conjunction and disjunction
For instance, if we want to check an LTL property "f" on paths that are weak fair in regard to the operations "a" and "b" and additionally strong fair in regard to "c" or "d", then this can be given as follows:
(WF(a) & WF(b)) & (SF(c) or SF(d)) => f
Note that the operators WF(-) and SF(-) cannot appear on the right side of the fairness implication. Basically, WF(-) and SF(-) can be described by the following equivalences:
WF(a) ≡ (FG e(a) => GF [a]) and SF(a) ≡ (GF e(a) => GF [a]), where a is an operation.
For setting fairness constraints on all possible operations of the model being checked use the operators "WEF" and "SEF". For instance, if "f" is a liveness property and we want to restrict the search only to strongly fair paths, then we can impose the fairness constraints by means of the formula "SEF => f".
The grammar for imposing fairness constraints by means of the fairness implication ("fair => f") looks as follows:
fair ::= WEF | SEF | wfair | sfair | wfair & sfair | sfair & wfair
wfair ::= wf(a) | ( wfair ) | wfair & wfair | wfair or wfair
sfair ::= sf(a) | ( sfair ) | sfair & sfair | sfair or sfair
where "a" is a transition proposition.
Storing LTL Assertions in the Model
Storing LTL formulas in B machines
LTL formulas can be stored in the `DEFINITIONS` section of a B machine. The name of the definition must start with `ASSERT_LTL` and a string must be specified. In case there is more than one LTL assertion given in the ‘DEFINITIONS’ section, the particular LTL assertions must be separated by semicolon. For example:
DEFINITIONS ASSERT_LTL == "G (e(SetCruiseSpeed) => e(CruiseBecomesNotAllowed))"; ASSERT_LTL1 == "G (e(CruiseBecomesNotAllowed) => e(SetCruiseSpeed))"; ASSERT_LTL2 == "G (e(CruiseBecomesNotAllowed) => (ObstacleDisappears))"
Storing LTL formulas in CSP-M specifications
LTL formulas can be stored within pragmas in CSP-M specifications. A pragma in which a single LTL formula is stored is given by "{-# assert_ltl "f" "c" #-}", where "assert_ltl" indicates the type of the information stored in the pragma (there are currently two types: assert_ltl and assert_ctl), and is followed by the LTL formula `f` and a comment `c` (the comment is optional). Both, the LTL formula and the comment, must be enclosed in double quotes.
It is also possible to give several LTL formulas in a single pragma within which the corresponding LTL assertions are separated by semicolon. For example:
{-# assert_ltl "SF(enter.1) & WF(req.1) => GF([enter.1])";
assert_ltl "SF(enter.2) & WF(req.2) => GF([enter.2])";
assert_ltl "GF [enter.1] & GF [enter.2]" "Should fail."#-}
Note that a semicolon must not follow the last assertion in a pragma.
For CSP-M specifications, it is also possible to assert LTL-formulae to particular processes in the model. This is possible by means of ``assert`` declarations, which have been recently included to the CSP-M grammar of the ProB CSP-M parser:
assert P |= LTL: "ltl-formula", where `P` is an arbitrary process and `ltl-formula` an LTL formula.
LTL Formulas in a Separate File
With the command line version of ProB it is possible to check several LTL[e] formulae with one call. The command has the following syntax
probcli -ltlfile FILE ...
The file FILE contains one or more sections where each section has the form
[Name] Formula
The formula itself can spread several lines. Additional comments can be added with a leading #. If a counter-example is found, the trace of the counter-example is saved into the file ltlce_Name.trace, where "Name" is the name of the formula in the LTL file.
One also can check a single LTL[e] formula F using the option '-ltlformula' as follows:
probcli -ltlformula "F" ...
LTL Formulae in a Separate File
With the command line version of ProB it is possible to check several LTL[e] formulae with one call. The command has the following syntax
probcli -ltlfile FILE ...
The file FILE contains one or more sections where each section has the form
[Name] Formula
The formula itself can spread in several lines. Additional comments can be added with a leading #. If a counter-example is found, the trace of the counter-example is saved into the file ltlce_Name.trace, where "Name" is the name of the formula in the LTL file.
One also can check a single LTL[e] formula F using the option '-ltlformula' as follows:
probcli -ltlformula "F" ...
LTL Model Checker Output
The output provided by the LTL model checker can sometimes reveal some interesting statistical facts about the model and the property being checked on the model. The LTL model checker of ProB uses the tableau approach for checking an LTL[e] formula on a formal model. To check whether a model M satisfies a given formula f, the algorithm generates a search graph, called also tableau graph, composed from the tableau of the formula and the state space of the model. If there is a path in the search graph that is a model for f, then the formula is satisfiable. The nodes of the search graph are called atoms.
Basically, using the tableau approach we prove that M satisfies f by negating the given formula and searching for a path fulfilling ¬f. If such a path is found, then we infer that M violates f. Otherwise, if no path is found that satisfies ¬f, we conclude that M |= f. The LTL model checking algorithm of ProB is based on searching for strongly connected components (SCCs) with certain properties to determine whether M satisfies f. Finding such an SCC that can be reached from an initial state of M is a witness for a counter-example for f. Sometimes, we use fairness to ignore such SCCs that do not fulfill the imposed fairness constraints in order to not impede proving a property by returning of non-fair paths as counter-examples.
The LTL model checker algorithm of ProB is implemented in C using a callback mechanism for evaluating the atomic propositions and the outgoing transitions in SICStus Prolog. (For each state of the model a callback will be performed.) Additionally, the search for SCCs is based on the Tarjan's algorithm. In the terminal all messages coming from the LTL model checker are preceded either by "LTL (current statistics): " or "LTL model checking:". The output from the LTL model checker can give helpful insights about the model and the model checking process.
Consider the CSP specifications "dphil_ltl8.csp" representing a model of the dining philosophers problem for eight philosophers which resolves the starvation problem by always forcing the first philosopher to pick up first the right fork instead of the left one. In other words, "dphil_ltl8.csp" has no deadlock states. Checking the LTL formula "GF [eat.0]" from the command line will produce the following output:
$ probcli -ltlformula "GF [eat.0]" dphil_ltl8.csp .... LTL model checking formula % parsing_ltl_formula % initialising_ltlc starting_model_checking LTL (current statistics): 13280 atoms, 10070 transitions generated, and 2631 callbacks needed. LTL model checking: found counter-example (lasso-form): intro length = 1126, path in SCC of length = 5 LTL model checking: memory usage approx. 1924 KiB, 14104 atoms and 10724 transitions generated LTL model checking: total time 22492ms, 2803 callbacks needed 22465ms, netto 26ms. ! An error occurred ! ! source(ltl) ! Model Check Counter-Example found for: ! GF [eat.0] Formula FALSE. Runtime: 22220 ms ! *** error occurred *** ! ltl
As one can clearly see from the output, the LTL model checker fails to prove "GF [eat.0]" on the model since it has found a counter-example for the formula. Note that the ProB LTL model checker explores the search graph and the state space dynamically. The above data is to be understand as follows:
- 14104 atoms - the LTL model checker needed to explore 14104 atoms to find a counter-example for the formula.
- 2803 callbacks needed - to explore the search graph the model checker makes callbacks in order to explore the state space of the model being checked (the exploration runs dynamically) and compute the successor states in the tableau graph. In this case the model checker has needed to explore 2803 states till it finds a counter-example for the formula
- memory usage approx. 1924 KiB - the memory needed to explore the tableau graph
- found counter-example (lasso-form) - means that the counter-example being found is path beginning in an initial state of the model and reaching a state that closes a cycle:
- intro length = 1126: the length of the sub-path from an initial state to the entry point of the cycle
- path in SCC of length = 5: the cycle is comprised of five states
- total time 22492ms - the LTL model checker needed about 23 seconds to find the counter-example. Here a distinction between the time needed to explore the state space of the model (2803 callbacks needed 22465ms) and the time spent for generating the tableau graph + the time for identifying the self-fulfilling SCC (netto 26ms)
- LTL (current statistics) - an intermediate data information is given each 20 seconds spent from the last current data information.
In the example above one can prove the LTL[e] formula "GF [eat.0]" on dphil_ltl6.csp using fairness. One can impose, for example, strong fairness conditions on all transitions of the model and thus verify that "GF [eat.0]" is satisfied under strong fairness. The call looks as follows:
$ probcli -ltlformula "SEF => GF [eat.0]" dphil_ltl8.csp ... LTL model checking formula % parsing_ltl_formula % initialising_ltlc starting_model_checking LTL (current statistics): 13016 atoms, 9834 transitions generated, and 2578 callbacks needed. LTL (fairness): 0 strongly connected components were rejected, 0 callbacks needed. LTL (current statistics): 27540 atoms, 44422 transitions generated, and 5123 callbacks needed. LTL (fairness): 284 strongly connected components were rejected, 843 callbacks needed. ..... LTL (current statistics): 85980 atoms, 267821 transitions generated, and 19733 callbacks needed. LTL (fairness): 454 strongly connected components were rejected, 1924 callbacks needed. LTL (current statistics): 95648 atoms, 364288 transitions generated, and 22150 callbacks needed. LTL (fairness): 773 strongly connected components were rejected, 3085 callbacks needed. LTL model checking: memory usage approx. 13829 KiB, 96500 atoms and 381625 transitions generated LTL model checking: total time 190887ms, 22363 callbacks needed 186690ms, netto 467ms. LTL model checking (fairness): 800 strongly connected components were rejected. LTL model checking (fairness): total fairness checking time 3729ms, 3246 callbacks needed 3452ms, netto 277ms. LTL Formula TRUE. No counter example found for SEF => GF [eat.0]. Runtime: 188370 ms
In the above check no fair counter-example could be found for the formula "GF [eat.0]". For this check the search graph comprises 96500 atoms and 381625 transitions, far more than the previous formula check (without fairness assumptions). Since no fair counter-example was found we can infer that the whole state space of the model was explored. Further, since we know from above that 22363 callbacks were needed to explore the search graph, we can infer that the state space of the model has in total 22363 states.
In the output above there is also some information about the fairness checking being performed for the model checker run. Form the fairness statistics we can see that the model checker has refuted 800 SCCs in total, i.e. there were 800 SCCs in the search graph that could serve as a counter-example for "GF [eat.0]" in case no fairness constraints were imposed.
Other Relevant Tutorials about LTL Model Checking
A brief tutorial on visualizing LTL counter-examples in the Rodin tool can be found here.
A tutorial of a simple case study, where setting fairness constraints to some of the LTL properties is required, can be found [[Mutual Exclusion (Fairness)|here]
Summary of CTL Syntax supported by ProB
CTL formulas f can be constructed from:
- atomic propositions:
{ Pred } to check if a B predicate Pred holds in the current state, e.g. {card(someset) > 1}
e(op) to check if an operation op is enabled
- propositional logic operators:
not f f or g f & g f => g
- temporal operators:
EX f there is a next state satisfying f
EX[Op] f there is a next state via Op satisfying f, e.g. EX[reset]{db={}}
AX f all next states satisfy f
EF f there exists a path where f holds in the future
EG f there exists a path where f holds globally
AF f for all paths f holds in the future
AG f for all paths f holds globally
E f U g there exists a path where f holds until g
Note: a model satisfies a CTL formula iff the formula holds in all initial states.
References
- ↑ O. Lichtenstein and A. Pnueli: Checking that Finite State Concurrent Programs Satisfy Their Linear Specification. POPL '85, Proceedings of the 12th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, ACM, 1985