Gilbreath Card Trick
My belief is that B is a very expressive language, which can be very convenient for modelling many problems. Hence, when in the Dagstuhl library I stumbled upon a nice short article by Tony Hoare and Natarajan Shankar in memory of Amir Pnueli, I decided to model the problem and time how long it would take me to solve the problem using ProB. The article unravels a card trick by Gilbreath. The card trick has several phases:
- first you arrange 16 cards into a sequence of quartets with one card from each suit (Spade, Club, Heart, Diamond) in the same order. The example in the article is as follows: ⟨5♠⟩,⟨3♡⟩,⟨Q♣⟩,⟨8♢⟩, ⟨K♠⟩,⟨2♡⟩,⟨7♣⟩,⟨4♢⟩, ⟨8♠⟩,⟨J♡⟩,⟨9♣⟩,⟨A♢⟩
- you split the cards into two sequences. The example in the article is: ⟨5♠⟩,⟨3♡⟩,⟨Q♣⟩,⟨8♢⟩,⟨K♠⟩ and ⟨2♡⟩,⟨7♣⟩,⟨4♢⟩,⟨8♠⟩,⟨J♡⟩,⟨9♣⟩,⟨A♢⟩ .
- you reverse one of the sequences
- you perform a (not necessarily perfect) riffle shuffle of the two sequences
- the resulting final sequence is guaranteed to consist of a sequence of four quartets with one card from each suite.
I attempted to model this problem in B and wanted to use model checking to validate the property on the final sequence. As I wanted to measure the time spent modeling I used a stopwatch. It took 13 minutes (starting from an empty B specification) to produce a first model that could be model checked by ProB. Full validation was finished after 19 minutes from the start. The model checking itself generated 150,183 states and 179,158 transitions and took 2 minutes and 17 seconds on a Mac Book Air (1.8 GHz i7). (Further below on this page I also describe ways to reduce the model checking time.) I am very interested in seeing how much combined modelling and verification time is required to solve this task in other formalisms and with other model checking tools (e.g., Promela with Spin, CSP with FDR, TLA+ with TLC).
Here is the specification
MACHINE CardTrick
/* Translation by Michael Leuschel of Example in
"Unraveling a Card Trick" by Tony Hoare and Natarajan Shankar
in LNCS 6200, pp. 195-201, 2010.
DOI: 10.1007/978-3-642-13754-9_10
https://link.springer.com/chapter/10.1007%2F978-3-642-13754-9_10
*/
SETS
SUIT={spade,club,heart,diamond}
DEFINITIONS
all == [spade,club,heart,diamond]; /* an arbitrary permutation of the suits */
/* check that in dst we can partition the deck into quartets where every suit occurs once: */
ok(dst) == #(a,b,c,d).(dst = a^b^c^d & size(a)=4 & size(b)=4 & size(c)=4 & size(d)=4 &
a : perm(SUIT) & b:perm(SUIT) & c:perm(SUIT) & d:perm(SUIT))
CONSTANTS
initial
PROPERTIES
initial = all^all^all^all /* we fix the sequence; i.e., we perform symmetry reduction by hand; it should be possible to achieve this by ProB's symmetry reduction itself using a deferred set */
VARIABLES x,y,dest,reversed
INVARIANT
x:seq(SUIT) & y:seq(SUIT) & dest:seq(SUIT) & reversed:BOOL &
((x=<> & y=<>) => ok(dest)) /* the property we are interested in: after the riffle shuffle the sequence consists of four quartets, each containing every suit */
INITIALISATION
x,y : (x^y = initial) /* split the initial sequence into two: x and y */
|| dest := <> || reversed := FALSE
OPERATIONS
/* reverse one of the two decks */
Reverse = PRE reversed=FALSE THEN CHOICE x := rev(x) OR y := rev(y) END || reversed := TRUE END;
/* perform the riffle shuffle: transfer one card from either x or y to dest */
Shuffle1 = PRE x/=<> & reversed=TRUE THEN dest := dest<-last(x) || x:= front(x) END;
Shuffle2 = PRE y/=<> & reversed=TRUE THEN dest := dest<-last(y) || y:= front(y) END
END
Some observations:
- in the above model I perform symmetry reduction by hand, by forcing a particular order of the cards initially
- a version of the model which does not do this can be found below; it requires symmetry reduction to be enabled for efficient model checking
- I have tried to translate this example to TLA+ and use TLC (using our new B-TLC translator), but TLC cannot deal with the initialisation x,y : (x^y = initial) . Later Domink Hansen produced an adapted (more low-level) version of my B machine which can be run by TLC; see below.
- A (longer) Why3 encoding can be found here http://proval.lri.fr/gallery/unraveling_a_card_trick.en.html.
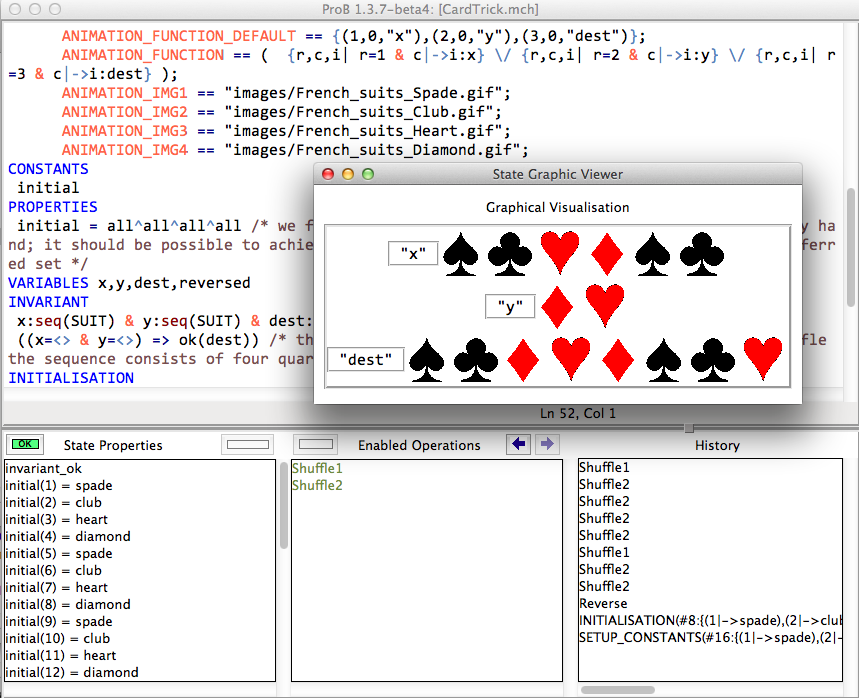
- Arguably model checking gives less insight into why the trick works than proof. However, by adding a graphical visualization, a different kind of insight can be gained. This is shown below.
Adding graphical visualization
To add a simple graphical visualization one needs to generate four pictures (in GIF format). I took pictures from Wikimedia Commons. In the DEFINITIONS section of the B machine above, you then simply have to add the following:
ANIMATION_FUNCTION_DEFAULT == {(1,0,"x"),(2,0,"y"),(3,0,"dest")};
ANIMATION_FUNCTION == ( {r,c,i| r=1 & c|->i:x} \/ {r,c,i| r=2 & c|->i:y} \/ {r,c,i| r=3 & c|->i:dest} );
ANIMATION_IMG1 == "images/French_suits_Spade.gif";
ANIMATION_IMG2 == "images/French_suits_Club.gif";
ANIMATION_IMG3 == "images/French_suits_Heart.gif";
ANIMATION_IMG4 == "images/French_suits_Diamond.gif";
Details about the use of this feature can be found in the Graphical_Visualization page of the manual. With the above, ProB will display the variables x, y and dist in a graphical way, and by animation one can gain insights into why it is impossible not to generate four quartets.
A version requiring symmetry reduction
MACHINE CardTrickSym /* a version to be used with ProB's symmetry reduction */
/* see comments in machine CardTrick for more details about the modeling effort */
/* Translation by Michael Leuschel of Example in "Unraveling a Card Trick" by Tony Hoare and Natarajan Shankar in LNCS 6200, pp. 195-201, 2010.
DOI: 10.1007/978-3-642-13754-9_10
https://link.springer.com/chapter/10.1007%2F978-3-642-13754-9_10
*/
/* Model checking with hash symmetry taking 161.9 seconds to traverse
150,183 states and 179,181 transitions (on a MacBook Air 1.8Ghz i7) */
SETS
SUIT /* ={spade,club,heart,diamond} */
DEFINITIONS
/* check that in dst we can partition the deck into quartets where every suit occurs once */
ok(dst) == #(a,b,c,d).(dst = a^b^c^d & size(a)=4 & size(b)=4 & size(c)=4 & size(d)=4 &
a : perm(SUIT) & b:perm(SUIT) & c:perm(SUIT) & d:perm(SUIT))
CONSTANTS
all
PROPERTIES
card(SUIT)=4 &
all : perm(SUIT) /* a sequence of all suits in any order */
VARIABLES x,y,dest,reversed
INVARIANT
x:seq(SUIT) & y:seq(SUIT) & dest:seq(SUIT) & reversed:BOOL &
((x=<> & y=<>) => ok(dest))
INITIALISATION x,y : (x^y = all^all^all^all ) || dest := <> || reversed := FALSE
OPERATIONS
Reverse = PRE reversed=FALSE THEN CHOICE x := rev(x) OR y := rev(y) END || reversed := TRUE END;
Shuffle1 = PRE x/=<> & reversed=TRUE THEN dest := dest<-last(x) || x:= front(x) END;
Shuffle2 = PRE y/=<> & reversed=TRUE THEN dest := dest<-last(y) || y:= front(y) END
END
A more low-level version for use with TLC
We later adapted the above model (without symmetry) to make it somewhat more low-level and to enable the translation to TLA+ for use with TLC (this is a new feature inside ProB Tcl/Tk). The machine is shown below. The model checking time with ProB is now reduced to 75 seconds. With the command "Verify -> External Tools -> Model Check with TLC..." you can use TLC as a backend. The model checking time is then approximately 15 seconds (including the translation time from B to TLA+).
MACHINE CardTrick_TLC
/* A version of the machine (adapted by Domink Hansen) which is a bit more low-level;
this improves model checking performance and now allows translation to TLC */
/* Translation by Michael Leuschel of Example in "Unraveling a Card Trick" by Tony Hoare and Natarajan Shankar in LNCS 6200, pp. 195-201, 2010.
DOI: 10.1007/978-3-642-13754-9_10
https://link.springer.com/chapter/10.1007%2F978-3-642-13754-9_10
*/
SETS
SUIT={spade,club,heart,diamond}
DEFINITIONS
all == [spade,club,heart,diamond];
/* check that in dst we can partition the deck into quartets where every suit occurs once */
subseq(s,m,n) == (s/|\n)\|/m-1;
ok(dst) == subseq(dst,1,4) : perm(SUIT)
& subseq(dst,5,8) : perm(SUIT)
& subseq(dst,9,12) : perm(SUIT)
& subseq(dst,13,16) : perm(SUIT);
/*#(a,b,c,d).(dst = a^b^c^d & size(a)=4 & size(b)=4 & size(c)=4 & size(d)=4 &
a : perm(SUIT) & b:perm(SUIT) & c:perm(SUIT) & d:perm(SUIT));*/
initial == all^all^all^all
/* we fix the sequence; i.e., we perform symmetry reduction by hand; it should be possible to achieve this by ProB's symmetry reduction itself using a deferred set */
VARIABLES x,y,dest,reversed
INVARIANT
x:seq(SUIT) & y:seq(SUIT) & dest:seq(SUIT) & reversed:BOOL &
((x=<> & y=<>) => ok(dest))
INITIALISATION x,y :(#n.(n : 0..size(initial) & x = initial /|\ n & y = initial \|/ n & x^y = initial)) || dest := <> || reversed := FALSE
OPERATIONS
Reverse = PRE reversed=FALSE THEN CHOICE x := rev(x) OR y := rev(y) END || reversed := TRUE END;
Shuffle1 = PRE x/=<> & reversed=TRUE THEN dest := dest<-last(x) || x:= front(x) END;
Shuffle2 = PRE y/=<> & reversed=TRUE THEN dest := dest<-last(y) || y:= front(y) END
END
The TLA+ translation generated by B-TLC is as follows:
---- MODULE CardTrick_TLC ----
EXTENDS Naturals, Sequences, SequencesExtended
CONSTANTS spade, club, heart, diamond
VARIABLES x, y, dest, reversed
SUIT == {spade, club, heart, diamond}
all == <<spade, club, heart, diamond>>
subseq(s, m, n) == DropFirstElements(TakeFirstElements(s, n), m - 1)
ok(dst) == subseq(dst, 1, 4) \in Perm(SUIT) /\ subseq(dst, 5, 8) \in Perm(SUIT) /\ subseq(dst, 9, 12) \in Perm(SUIT) /\ subseq(dst, 13, 16) \in Perm(SUIT)
initial == all \o all \o all \o all
Invariant == x \in Seq(SUIT) /\ y \in Seq(SUIT) /\ dest \in Seq(SUIT) /\ reversed \in BOOLEAN /\ (x = <<>> /\ y = <<>> => ok(dest))
Init == \E n \in (0 .. Len(initial)) : n \in (0 .. Len(initial)) /\ x = TakeFirstElements(initial, n) /\ y = DropFirstElements(initial, n) /\ x \o y = initial
/\ dest = <<>>
/\ reversed = FALSE
Reverse == reversed = FALSE
/\ ((x' = Rev(x) /\ UNCHANGED <<y>>) \/ (y' = Rev(y) /\ UNCHANGED <<x>>))
/\ reversed' = TRUE /\ UNCHANGED <<dest>>
Shuffle1 == (x # <<>> /\ reversed = TRUE)
/\ dest' = Append(dest, Last(x))
/\ x' = Front(x) /\ UNCHANGED <<y, reversed>>
Shuffle2 == (y # <<>> /\ reversed = TRUE)
/\ dest' = Append(dest, Last(y))
/\ y' = Front(y) /\ UNCHANGED <<x, reversed>>
Next == \/ Reverse
\/ Shuffle1
\/ Shuffle2
====