Die Hard Jugs Puzzle
This is the B model of a puzzle from the movie "Die Hard with a Vengeance". This shows Bruce Willis and Samuel Jackson having a go at the puzzle. A detailed explanation can be found here. At start we have one 3 gallon and one 5 gallon jug, and we need to measure precisely 4 gallons by filling, emptying or transferring water from the jugs.
MACHINE Jars
DEFINITIONS
GOAL == (4:ran(level));
SETS Jars = {j3,j5}
CONSTANTS maxf
PROPERTIES maxf : Jars --> NATURAL &
maxf = {j3 |-> 3, j5 |-> 5} /* in this puzzle we have two jars, with capacities 3 and 5 */
VARIABLES level
INVARIANT
level: Jars --> NATURAL
INITIALISATION level := Jars * {0} /* all jars start out empty */
OPERATIONS
FillJar(j) = /* we can completely fill a jar j */
PRE j:Jars & level(j)<maxf(j) THEN
level(j) := maxf(j)
END;
EmptyJar(j) = /* we can completely empty a jar j */
PRE j:Jars & level(j)>0 THEN
level(j) := 0
END;
Transfer(j1,amount,j2) = /* we can transfer from jar j1 to j2 until either j2 is full or j1 is empty */
PRE j1:Jars & j2:Jars & j1 /= j2 & amount>0 &
amount = min({level(j1), maxf(j2)-level(j2)}) THEN
level := level <+ { j1|-> level(j1)-amount, j2 |-> level(j2)+amount }
END
END
After opening the file in ProB, choose the Model Check command in the Verify menu and then check the "Find Define GOAL" check box. This instructs ProB to search for states satisfying the GOAL predicate (4:ran(level)) defined above.
Now press the model check button and you should now obtain the following message:

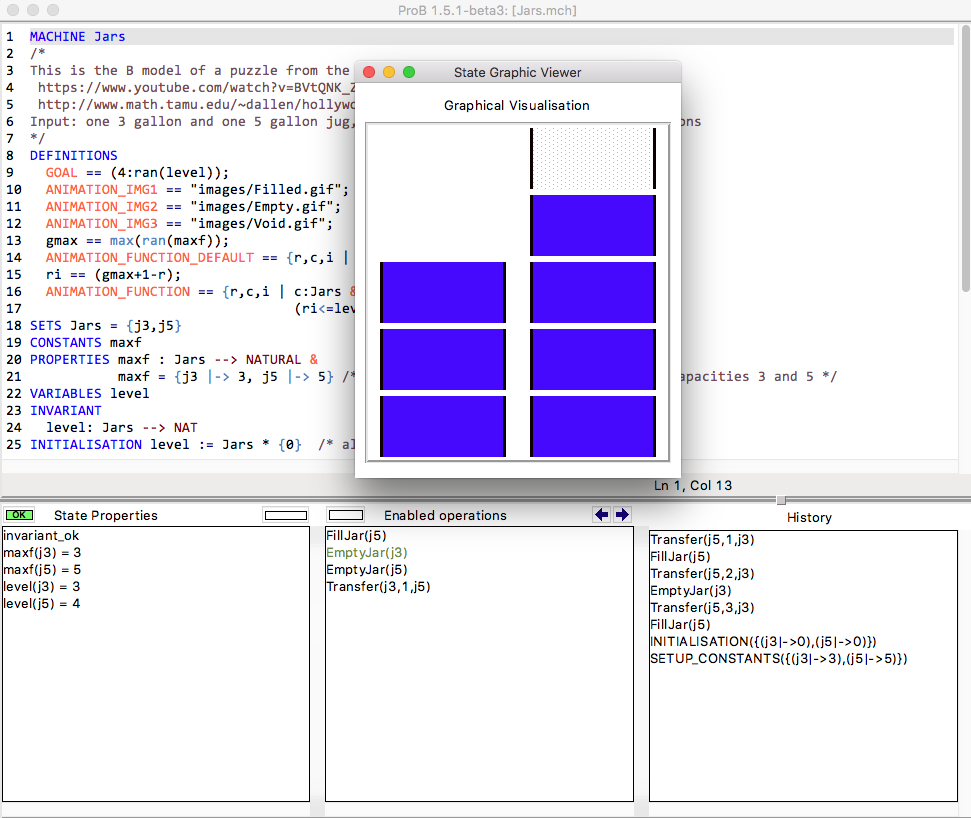
The main window of ProB now contains the following information:

You can see that the second jug contains exactly 4 gallons. The steps required to reach this state can be found in the history pane on the right (in reverse order).
Graphical Animation
This machine above is actually included in the ProB distribution (inside the examples/B/GraphicalAnimation/ directory). It also contains the following lines in the DEFINITIONS section, which defines a quick-and-dirty graphical visualisation of the state. The images can be found in the subfolder images along the file Jars.mch.
ANIMATION_IMG1 == "images/Filled.gif";
ANIMATION_IMG2 == "images/Empty.gif";
ANIMATION_IMG3 == "images/Void.gif";
gmax == max(ran(maxf));
ANIMATION_FUNCTION_DEFAULT == {r,c,i | c:Jars & r:1..gmax & i=3};
ri == (gmax+1-r);
ANIMATION_FUNCTION == {r,c,i | c:Jars & ri:1..maxf(c) &
(ri<=level(c) => i=1 ) & (ri>level(c) => i=2)}
Here is a screenshot of ProB Tcl/Tk after loading the model and having found the goal:
Using probcli (command-line version)
To find the solution using probcli you just need to type:
probcli -model_check Jars.mch
The output will be as follows:
$ probcli -model_check Jars.mch
% found_enumeration_of_constants(30,40)
% backtrack(found_enumeration_of_constants(30,40))
ALL OPERATIONS COVERED
found_error(goal_found,10)
finding_trace_from_to(root)
.
Model Checking Time: 60 ms (60 ms walltime)
States analysed: 10
Transitions fired: 36
*** COUNTER EXAMPLE FOUND ***
goal_found
*** TRACE:
1: SETUP_CONSTANTS({(j3|->3),(j5|->5)}):
2: INITIALISATION({(j3|->0),(j5|->0)}):
3: FillJar(j5):
4: Transfer(j5,3,j3):
5: EmptyJar(j3):
6: Transfer(j5,2,j3):
7: FillJar(j5):
8: Transfer(j5,1,j3):
! *** error occurred ***
! goal_found
Z Version
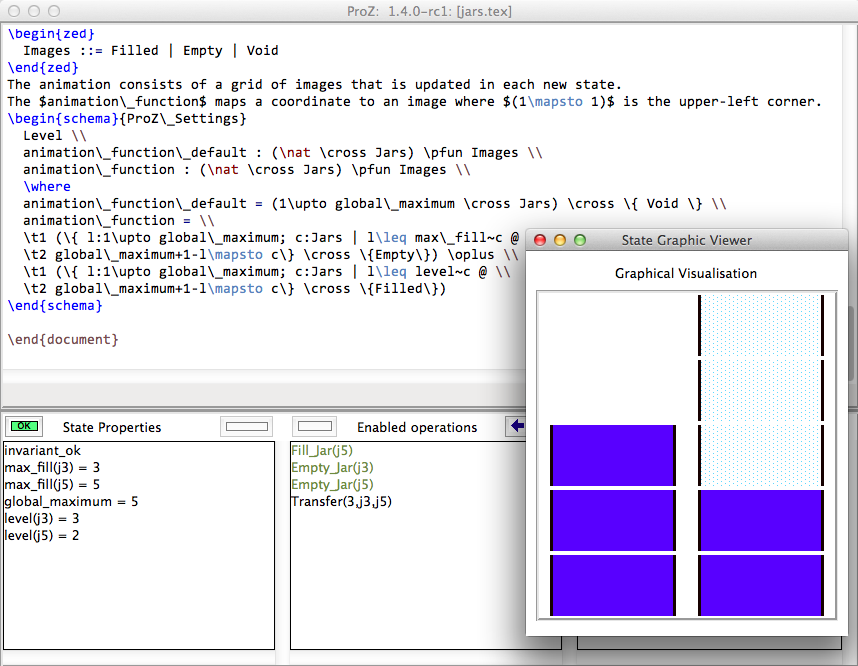
A Z version of the puzzle is also included with ProB (inside the examples/Z/GraphicalAnimation/ directory) and shown on the ProZ wiki page.
Here is how the animation of the Z specification should look like: