Cheryl's Birthday: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
In case you are new to B, you probably need to know the following operators to understand the specification below (we als have a [[Summary_of_B_Syntax|summary page about the B syntax]]): | In case you are new to B, you probably need to know the following operators to understand the specification below (we als have a [[Summary_of_B_Syntax|summary page about the B syntax]]): | ||
* <tt>x : S</tt> specifies that x is an element of S | * <tt>x : S</tt> specifies that x is an element of S | ||
* <tt>dom(r)</tt> is the domain of a function or relation | * <tt>dom(r)</tt> is the domain of a function or relation r | ||
* <tt>r~</tt> is the inverse of a function or relation | * <tt>r~</tt> is the inverse of a function or relation r | ||
* <tt>r[S]</tt> is the relational image of a relation r for a set of domain values S | * <tt>r[S]</tt> is the relational image of a relation r for a set of domain values S | ||
* <tt>card(S)</tt> is the cardinality of a set | * <tt>card(S)</tt> is the cardinality of a set S | ||
* <tt>a|->b</tt> represents the pair (a,b); note that a relation and function in B is a set of pairs. | * <tt>a|->b</tt> represents the pair (a,b); note that a relation and function in B is a set of pairs. | ||
* <tt>!x.(P => Q)</tt> denotes universal quantification over variable x | * <tt>!x.(P => Q)</tt> denotes universal quantification over variable x | ||
<pre> | <pre> | ||
Latest revision as of 09:22, 18 April 2015
This Puzzle is a variation of another Puzzle (Sum and Product) and has been described in a New York Times article.
Here is a first solution in B, where the text of the puzzle has been integrated as comments. There are almost certainly more elegant encodings of the problem in B. You can load this model using, e.g., ProB Tcl/Tk (see below). The model is also available as an example in our online ProB Logic Calculator.
In case you are new to B, you probably need to know the following operators to understand the specification below (we als have a summary page about the B syntax):
- x : S specifies that x is an element of S
- dom(r) is the domain of a function or relation r
- r~ is the inverse of a function or relation r
- r[S] is the relational image of a relation r for a set of domain values S
- card(S) is the cardinality of a set S
- a|->b represents the pair (a,b); note that a relation and function in B is a set of pairs.
- !x.(P => Q) denotes universal quantification over variable x
MACHINE CherylsBirthday
/* A simplified version of the SumProduct Puzzle taken from
http://www.nytimes.com/2015/04/15/science/a-math-problem-from-singapore-goes-viral-when-is-cheryls-birthday.html
*/
DEFINITIONS
DontKnowFromDay(PossDates,KDay) == card(PossDates~[{KDay}]) > 1;
KnowFromDay(PossDates,KDay) == card(PossDates~[{KDay}]) = 1
CONSTANTS Month, Day, PD, PD2
PROPERTIES
/* Albert and Bernard just met Cheryl. “When’s your birthday?” Albert asked Cheryl.*/
Month:STRING & Day:1..31 &
/* Cheryl thought a second and said, “I’m not going to tell you, but I’ll give you some clues.” She wrote down a list of 10 dates: */
PD = {("aug"|->14),("aug"|->15),("aug"|->17),
("july"|->14),("july"|->16),("june"|->17),("june"|->18),
("may"|->15),("may"|->16),("may"|->19)}
&
/*
Then Cheryl whispered in Albert’s ear the month — and only the month — of her birthday.
To Bernard, she whispered the day, and only the day.
*/
Month : dom(PD) &
Day : ran(PD) &
Month|->Day : PD &
/* Albert: I don’t know when your birthday is, */
card(PD[{Month}]) > 1 &
/* but I know Bernard doesn’t know, either. */
!x.(x:PD[{Month}] => DontKnowFromDay(PD,x) ) &
/* Bernard: I didn’t know originally, */
DontKnowFromDay(PD,Day) &
/* but now I do. */
PD2 = {m,d| (m|->d):PD & !x.(x:PD[{m}] => DontKnowFromDay(PD,x) ) } &
KnowFromDay(PD2,Day) &
/* Albert: Well, now I know, too! */
card({d|Month|->d : PD2 & KnowFromDay(PD2,d)})=1
ASSERTIONS /* single solution found by ProB in 20-30 ms */
Month = "july";
Day = 16
END
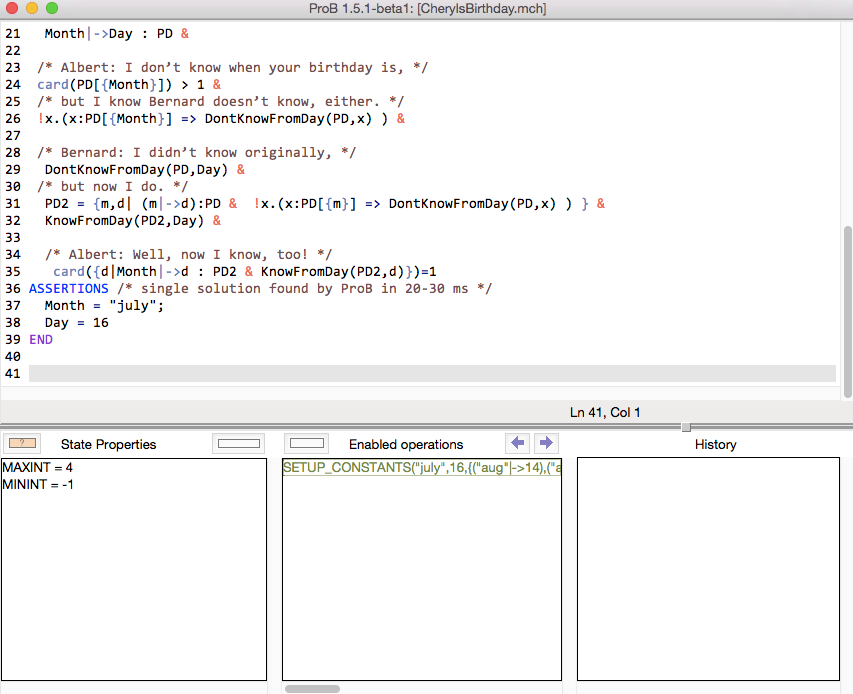
When loading this B machine in ProB, you will see that there is only a single solution (solving time 20-30 ms) : Month = "july" and Day = 16.
Here is a screenshot of ProB Tcl/Tk after loading the model.
Using an enumerated set
It is possible to use an enumerated set for the Months. One simply has to add
SETS MONTHS = {may, june, july, aug, sep}
and then change the definition of the possible dates:
PD = {(aug|->14), (aug|->15), (aug|->17),
(july|->14),(july|->16),(june|->17),
(june|->18),
(may|->15),(may|->16),(may|->19)}
and also "july" in the ASSERTIONS clause into july. This makes constraint solving via ProB marginally faster.