B2SAT: Difference between revisions
No edit summary |
|||
| Line 115: | Line 115: | ||
[[File:IceCream_Generic.pdf|500px|center]] | [[File:IceCream_Generic.pdf|500px|center]] | ||
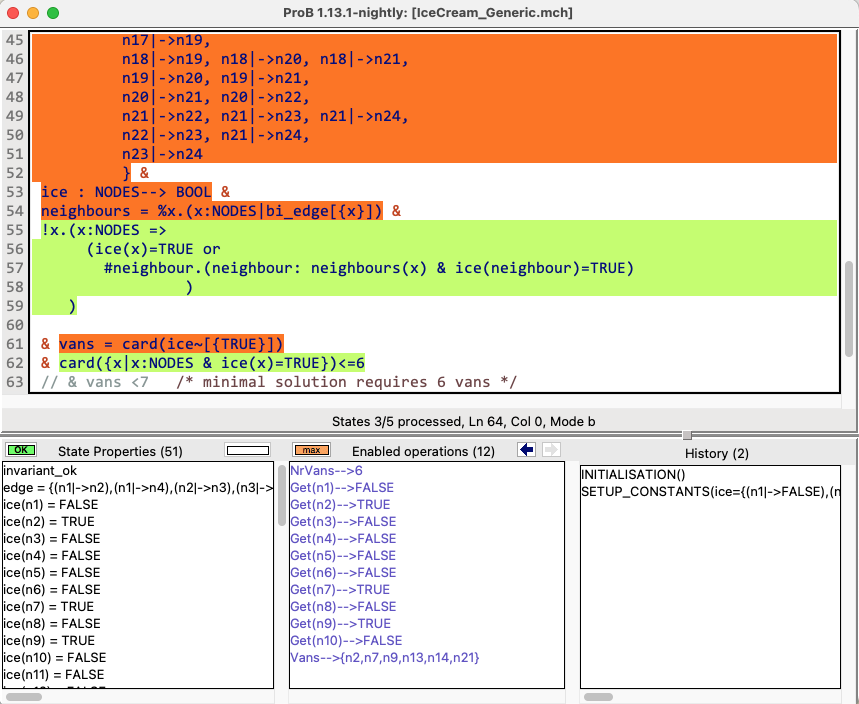
By choosing "Show Source Code Coverage" in the Debug menu of ProB Tcl/Tk you can see which parts of the properties were translated to SAT (in green) and which were processed entirely by ProB (in red-orange): | |||
Here is the graphical rendering of a solution using the custom graph definition above: | |||
[[File:IceCreamCoverage.png|500px|center]] | |||
=== B2SAT in Jupyter Notebooks === | === B2SAT in Jupyter Notebooks === | ||
Revision as of 07:28, 24 April 2024
The current versions of ProB can make use of the new B2SAT backend as an alternate way of solving constraints. It translates a subset of B formulas to SAT and for solving by an external SAT solver. The new backend interleaves low-level SAT solving with high-level constraint solving performed by the default solver of ProB.
B2SAT solving consists of the following phases:
- the deterministic propagation phase(s) of ProB's solver: it performs deterministic propagations and can expand quantifiers and total functions.
- a compilation phase, whereby static values are inlined.
- the B to CNF conversion proper, which can translate a subset of B to propositional logic in conjunctive normal form. This phase currently supports:
- equalities and inequalities between boolean variables and constants,
- all logical connectives and
- some cardinality constraints.
- Subformulas that cannot be solved are sent to ProB's default solver and linked to the CNF via an auxiliary propositional variable.
- solving phase, where the generated CNF is sent to an external SAT solver.
- propagation of the SAT solution to B, by progressively grounding the B values and predicates linked to the propositional variables.
- complete constraint solving, solving the pending constraints in B by now performing the regular non-deterministic propagations and enumerations of ProB.
Using B2SAT
B2SAT in the REPL
The following four commands are now available in REPL of probcli (start with probcli --repl):
- :sat PRED
- :sat-z3 PRED
- :sat-double-check PRED
- :sat-z3-double-check PRED
Here is a simple example:
>>> :sat f:1..n --> BOOL & n=3 & f(1)=TRUE & !i.(i:2..n => f(i) /= f(i-1))
PREDICATE is TRUE
Solution:
f = {(1|->TRUE),(2|->FALSE),(3|->TRUE)} &
n = 3
B2SAT for PROPERTIES
The new preference SOLVER_FOR_PROPERTIES can be used to specify solver for PROPERTIES (axioms) when setting up constants. The valid settings are: prob (the default), kodkod, z3, z3cns, z3axm, cdclt, sat, sat-z3.
The last two will use B2SAT, {\tt sat} with Glucose as SAT solver and {\tt sat-z3} with Z3 as SAT solver.
Here is an example using this preference:
MACHINE IceCream_Generic
// Dominating set example:
// place ice cream vans so that every house (node) is at most one block away from a van
// a version which can be solved by B2SAT
DEFINITIONS
N == 24;
CUSTOM_GRAPH == rec(layout:"dot", rankdir:"TB",
nodes: {j•j:NODES |
rec(value:j, style:"filled",
fillcolor:IF ice(j)=TRUE THEN "mistyrose" ELSE "white" END
)},
edges:rec(color:"gray", arrowhead:"odot",
arrowtail:"odot", dir:"both",
label:"edge", edges: edge)
);
bi_edge == (edge \/ edge~);
SET_PREF_SMT == TRUE;
SET_PREF_TIME_OUT == 50000;
SET_PREF_SOLVER_STRENGTH == 300;
SET_PREF_SOLVER_FOR_PROPERTIES == "sat";
SETS
NODES = {n1,n2,n3,n4,n5,n6,n7,n8,n9,n10,
n11,n12,n13,n14,n15,n16,n17,n18,n19,n20,n21,n22,n23,n24}
CONSTANTS edge, ice, vans, neighbours
PROPERTIES
edge: NODES <-> NODES &
edge = { n1|->n2, n1|->n4,
n2|->n3,
n3|->n4, n3|->n5, n3|->n7,
n4|->n7,
n5|->n6, n5|->n9,
n6|->n7, n6|->n8,
n7|->n8,
n8|->n10, n8|->n13,
n9|->n10, n9|->n11, n9|->n12,
n11|->n12, n11|->n14,
n12|->n13,
n13|->n16,
n14|->n15, n14|->n17,
n15|->n16, n15|->n17, n15|->n18, n15|->n21,
n16|->n18, n16|->n19,
n17|->n19,
n18|->n19, n18|->n20, n18|->n21,
n19|->n20, n19|->n21,
n20|->n21, n20|->n22,
n21|->n22, n21|->n23, n21|->n24,
n22|->n23, n21|->n24,
n23|->n24
} &
ice : NODES--> BOOL &
neighbours = %x.(x:NODES|bi_edge[{x}]) &
!x.(x:NODES =>
(ice(x)=TRUE or
#neighbour.(neighbour: neighbours(x) & ice(neighbour)=TRUE)
)
)
& vans = card(ice~[{TRUE}])
& card({x|x:NODES & ice(x)=TRUE})<=6 /* minimal solution requires 6 vans */
OPERATIONS
v <-- NrVans = BEGIN v := vans END;
xx <-- Get(yy) = PRE yy:NODES THEN xx:= ice(yy) END;
v <-- Vans = BEGIN v:= ice~[{TRUE}] END
END
Here is the graphical rendering of a solution using the custom graph definition above:
By choosing "Show Source Code Coverage" in the Debug menu of ProB Tcl/Tk you can see which parts of the properties were translated to SAT (in green) and which were processed entirely by ProB (in red-orange):
Here is the graphical rendering of a solution using the custom graph definition above:
B2SAT in Jupyter Notebooks
The solve command in the ProB Jupyter kernel now supports sat and satz3 as solvers. They use B2SAT with Glucose and Z3 as SAT solvers respectively.
Here is a simple example to solve a constraint:

This shows how you can use cardinality constraints to iteratively find a minimal dominating set D of a graph g:


