Apples and Oranges (Apple Interview Question)
This puzzle is apparently an Interview question at Apple. Quoting from [1] we have the following information:
- (1) There are three boxes, one contains only apples, one contains only oranges, and one contains both apples and oranges.
- (2) The boxes have been incorrectly labeled such that no label identifies the actual contents of the box it labels.
- (3) Opening just one box, and without looking in the box, you take out one piece of fruit.
- (4) By looking at the fruit, how can you immediately label all of the boxes correctly?
Here is one encoding of this puzzle in B:
MACHINE ApplesOranges
SETS
Fruit={apple,orange}; // possible content for the boxes
Label={A,O,Both} // labels for the boxes
CONSTANTS a,o,b, // a,o,b are the three boxes
Take, // which box should we open (the label of that box)
DecisionFunction // given the fruit we pick from Take: what are the contents of the boxes labeled A,O,Both
PROPERTIES
a = {apple} & o={orange} & b={apple,orange} // (1)
&
Take : Label //3
&
DecisionFunction : Fruit --> (Label >->> {a,o,b}) & //4
!label. ( // the decision function has to work for all allowed labelings
( label : {a,o,b} >->> Label &
label(a) /= A & label(o) /= O & label(b) /= Both // (2)
)
=>
!f.(f: label~(Take)
=> DecisionFunction(f)=label~ // the function should tell us what is behind label A,O,Both
)
)
END
We have abstracted the box of apples a by the set containing apple. Ditto for o and b, which are abstracted by {orange} and {apple,orange} respectively.
Note: you need a recent version of ProB 1.5.1-beta3 or newer to load the above model with its one-line comments. If you have an older version of ProB, simply use the normal comments /* ... */.
Loading this model with ProB gives you just one solution (after less than 10 ms):
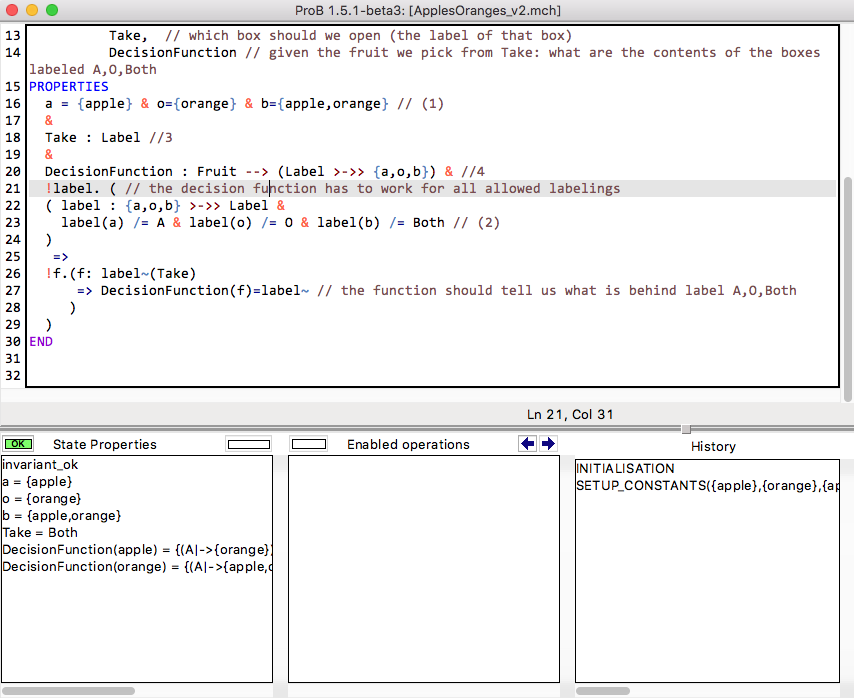
As we can see, the only solution is to open the box labelled with "Both". We can inspect the decision function by using the B REPL (e.g., double click on the State Properties pane to open it):
>>>> DecisionFunction(apple)
{(A|->{orange}),(O|->{apple,orange}),(Both|->{apple})}
>>>> DecisionFunction(orange)
{(A|->{apple,orange}),(O|->{apple}),(Both|->{orange})}
In other words, when we pick an apple out of the box labelled with "Both", then it contains only apples and the box labelled "O"ranges contains both apples and oranges. The box labelled "A"pples contains just oranges. Similarly, if we pick up an orange out of the box labelled with "Both", then it contains only oranges and the box labelled with "A"pples contains contains both apples and oranges. The box labelled "O"ranges contains just apples.
Note: you can inspect values or expressions in a tabular form, using the command "Expression as Table..." in the Visualize->Formulas menu. If you enter "DecisionFunction" as expression you will see the following tabular representation:
