Alloy
As of version 1.8 ProB provides support to load Alloy models.
The Alloy models are translated to B machines by a Java frontend.
This work and web page is still experimental.
The work is based on a translation of the specification language Alloy to classical B. The translation allows us to load Alloy models into ProB in order to find solutions to the model's constraints. The translation is syntax-directed and closely follows the Alloy grammar. Each Alloy construct is translated into a semantically equivalent component of the B language. In addition to basic Alloy constructs, our approach supports integers and orderings.
Installation
Alloy2B is included with the lastest nightly builds of ProB.
You can build it yourself:
- Clone or download Alloy2B project on Github.
- Make jar file (gradle build) and
- put resulting alloy2b-*.jar file into ProB's lib folder.
Examples
N-Queens
module queens
open util/integer
sig queen { x:Int, x':Int, y:Int } {
x >= 1
y >= 1
x <= #queen
y <= #queen
x' >=1
x' <= #queen
x' = minus[plus[#queen,1],x]
}
fact { all q:queen, q':(queen-q) {
! q.x = q'.x
! q.y = q'.y
! plus[q.x,q.y] = plus[q'.x,q'.y]
! plus[q.x',q.y] = plus[q'.x',q'.y]
}}
pred show {}
run show for exactly 4 queen, 5 int
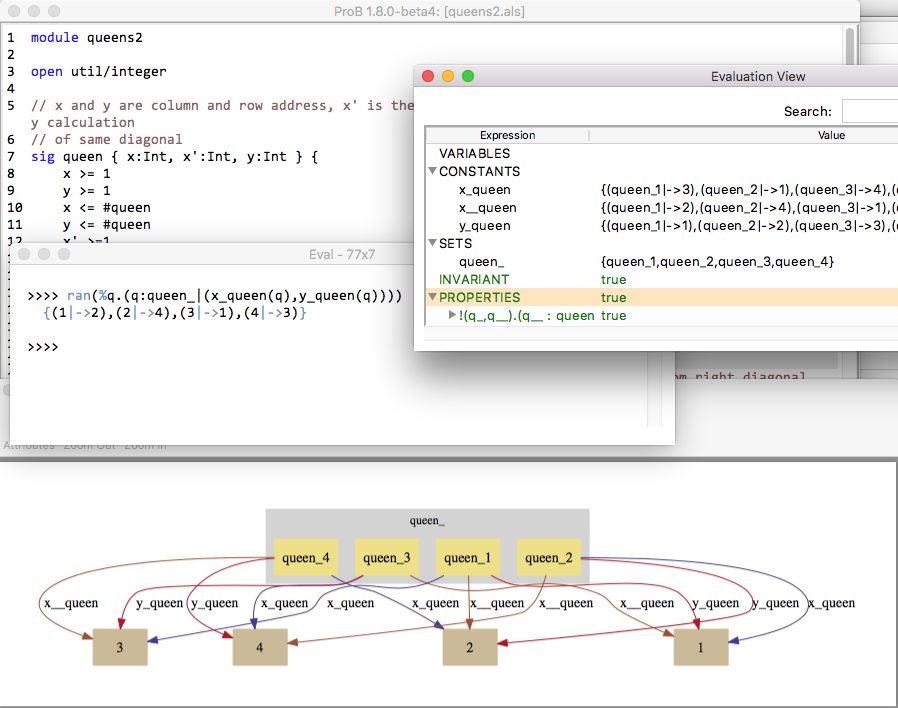
This can be loaded in ProB, as shown in the following screenshot. To run the "show" command you have to use "Find Sequence..." command for "run_show" in the "Constraint-Based Checking" submenu of the "Verify" menu.
Internally the Alloy model is translated to the following B model:
/*@ generated */
MACHINE queens
SETS queen_
CONSTANTS x_queen, x__queen, y_queen
DEFINITIONS
show_ == 1=1 ;
SET_PREF_MAXINT == 15 ; SET_PREF_MININT == -16
PROPERTIES
(!(q_, q__).({q_} <: queen_ & {q__} <: (queen_ - {q_}) =>
(not((x_queen(q_) = x_queen(q__)))) & (not((y_queen(q_) = y_queen(q__))))
& (not(((x_queen(q_) + y_queen(q_)) = (x_queen(q__) + y_queen(q__)))))
& (not(((x__queen(q_) + y_queen(q_)) = (x__queen(q__) + y_queen(q__))))))) &
card(queen_) = 4 &
/* from signature declaration */ !(this_).({this_} <: queen_ =>
((x_queen(this_) >= 1)) & ((y_queen(this_) >= 1))
& ((x_queen(this_) <= card(queen_)))
& ((y_queen(this_) <= card(queen_)))
& ((x__queen(this_) >= 1)) & ((x__queen(this_) <= card(queen_)))
& ((x__queen(this_) = ((card(queen_) + 1) - x_queen(this_))))) &
x_queen : queen_ --> INT &
x__queen : queen_ --> INT &
y_queen : queen_ --> INT
OPERATIONS
run_show = PRE show_ THEN skip END
END
River Crossing Puzzle
module river_crossing
open util/ordering[State]
abstract sig Object { eats: set Object }
one sig Farmer, Fox, Chicken, Grain extends Object {}
fact { eats = Fox->Chicken + Chicken->Grain}
sig State { near, far: set Object }
fact { first.near = Object && no first.far }
pred crossRiver [from, from', to, to': set Object] {
one x: from | {
from' = from - x - Farmer - from'.eats
to' = to + x + Farmer
}
}
fact {
all s: State, s': s.next {
Farmer in s.near =>
crossRiver [s.near, s'.near, s.far, s'.far]
else
crossRiver [s.far, s'.far, s.near, s'.near]
}
}
run { last.far=Object } for exactly 8 State
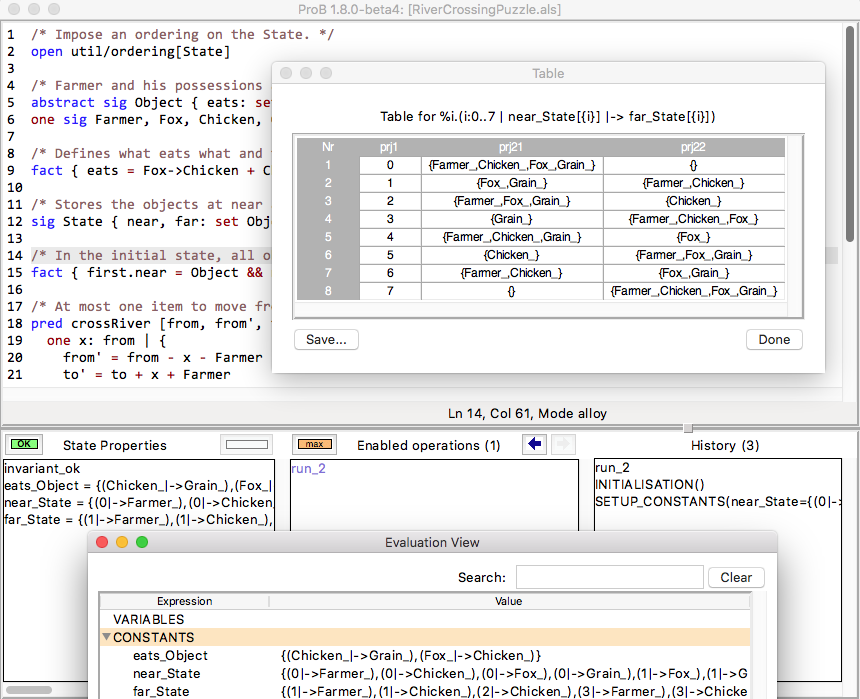
This can be loaded in ProB, as shown in the following screenshot. To run the "show" command you have to use "Find Sequence..." command for "run_show" in the "Constraint-Based Checking" submenu of the "Verify" menu (after enabling Kodkod in the Preferences menu).
Internally the Alloy model is translated to the following B model:
/*@ generated */
MACHINE river_crossing
SETS
Object_
CONSTANTS
Farmer_, Fox_, Chicken_, Grain_, eats_Object, near_State, far_State
DEFINITIONS
crossRiver_(from_,from__,to_,to__) == from_ <: Object_
& from__ <: Object_ & to_ <: Object_
& to__ <: Object_ & (card({x_ | {x_} <: from_
& (((from__ = (((from_ - {x_}) - {Farmer_}) - eats_Object[from__])))
& ((to__ = ((to_ \/ {x_}) \/ {Farmer_}))))}) = 1) ;
next_State_(s) == {x|x=s+1 & x:State_} ;
nexts_State_(s) == {x|x>s & x:State_} ;
prev_State_(s) == {x|x=s-1 & x:State_} ;
prevs_State_(s) == {x|x<s & x:State_} ;
State_ == 0..7
PROPERTIES
{Farmer_} <: Object_ &
{Fox_} <: Object_ &
{Chicken_} <: Object_ &
{Grain_} <: Object_ &
((eats_Object = (({Fox_} * {Chicken_}) \/ ({Chicken_} * {Grain_})))) &
(((near_State[{min(State_)}] = Object_) & far_State[{min(State_)}] = {})) &
(!(s_, s__).({s_} <: State_ & {s__} <: next_State_(s_) =>
((({Farmer_} <: near_State[{s_}]) =>
crossRiver_(near_State[{s_}], near_State[{s__}],
far_State[{s_}], far_State[{s__}]))
& (not(({Farmer_} <: near_State[{s_}])) =>
crossRiver_(far_State[{s_}], far_State[{s__}],
near_State[{s_}], near_State[{s__}]))))) &
Farmer_ /= Fox_ &
Farmer_ /= Chicken_ &
Farmer_ /= Grain_ &
Fox_ /= Chicken_ &
Fox_ /= Grain_ &
Chicken_ /= Grain_ &
{Farmer_} \/ {Fox_} \/ {Chicken_} \/ {Grain_} = Object_ &
eats_Object : Object_ <-> Object_ &
near_State : State_ <-> Object_ &
far_State : State_ <-> Object_
OPERATIONS
run_2 = PRE (far_State[{max(State_)}] = Object_) THEN skip END
END
Proof with Atelier-B Example
sig Object {}
sig Vars {
src,dst : Object
}
pred move (v, v': Vars, n: Object) {
v.src+v.dst = Object
n in v.src
v'.src = v.src - n
v'.dst = v.dst + n
}
assert add_preserves_inv {
all v, v': Vars, n: Object |
move [v,v',n] implies v'.src+v'.dst = Object
}
check add_preserves_inv for 3
Note that our translation does not (yet) generate an idiomatic B encoding, with move as B operation
and src+dst=Object as invariant: it generates a check operation encoding the predicate add_preserves_inv with universal quantification.
Below we shoe the B machine we have input into AtelierB. It was obtained by pretty-printing from \prob, and putting the negated guard
of theadd_preserves_inv into an assertion (so that AtelierB generates the desired proof obligation).
MACHINE alloytranslation
SETS /* deferred */
Object_; Vars_
CONCRETE_CONSTANTS
src_Vars, dst_Vars
PROPERTIES
src_Vars : Vars_ --> Object_
& dst_Vars : Vars_ --> Object_
ASSERTIONS
!(v_,v__,n_).(v_ : Vars_ & v__ : Vars_ & n_ : Object_
=>
(src_Vars[{v_}] \/ dst_Vars[{v_}] = Object_ &
v_ |-> n_ : src_Vars &
src_Vars[{v__}] = src_Vars[{v_}] - {n_} &
dst_Vars[{v__}] = dst_Vars[{v_}] \/ {n_}
=>
src_Vars[{v__}] \/ dst_Vars[{v__}] = Object_)
)
END
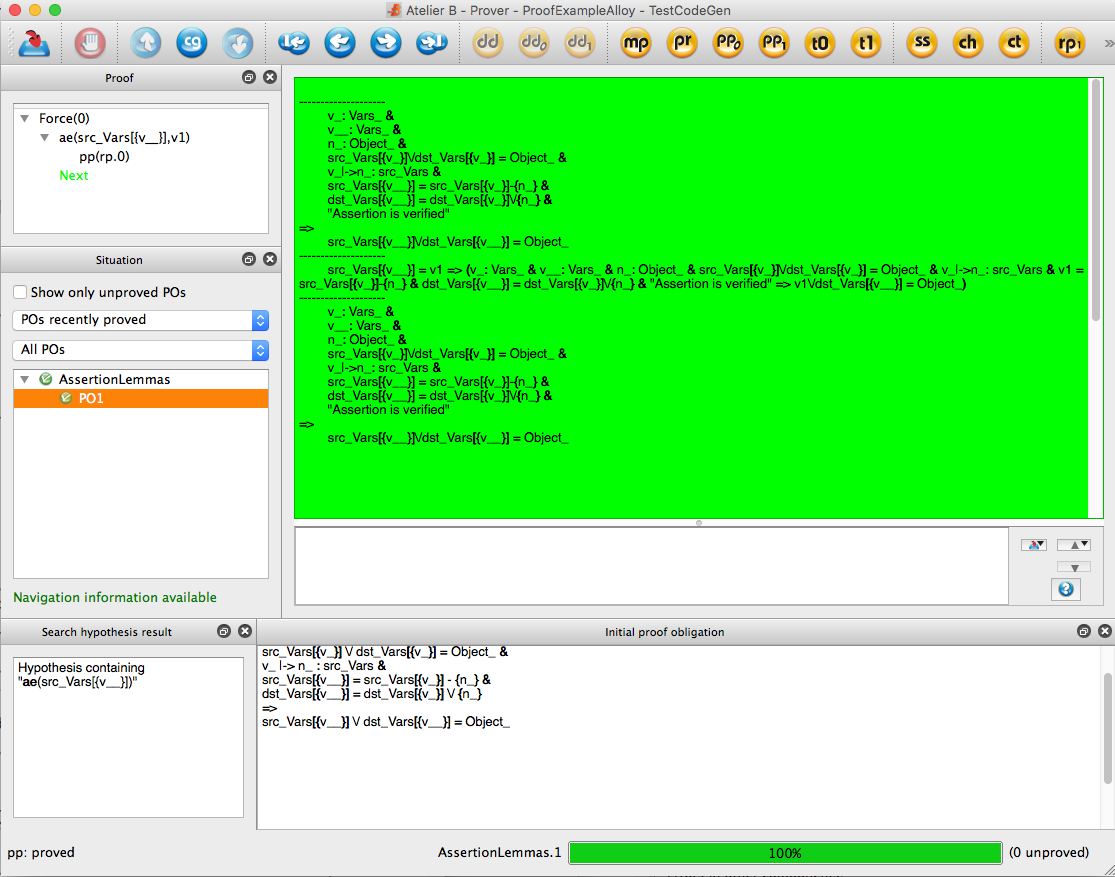
The following shows AtelierB proving the above assertion:
Alloy Syntax
Logical predicates: ------------------- P and Q conjunction P or Q disjunction P implies Q implication P iff Q equivalence not P negation all x:S | P universal quantification some x:S | P existential quantification some disjoint x,y : S | P Alternative syntax: P && Q conjunction P || Q disjunction P => Q implication P <=> Q equivalence ! P negation Set Expressions: ---------------- univ all objects none empty set S + T set union S & T set intersection S - T set difference # S cardinality of set Set Predicates: --------------- no S set S is empty S in T R is subset of S S = T set equality some S set S is not empty one S S is singleton set lone S S is empty or a singleton Relation Expressions: ---------------------- R -> S Cartesian product R . S relational join S <: R domain restriction of relation R for unary set S R :> S range restriction of relation R for unary set S ~R relational inverse ^R transitive closure of binary relation *R reflexive and transitive closure Arithmetic Expressions and Predicates: -------------------------------------- You need to open util/integer: plus[X,Y] addition minus[X,Y] subtraction mul[X,Y] multiplication div[X,Y] division rem[X,Y] remainder sum[S] sum of integers of set S X < Y less X = Y integer equality X > Y greater X =< Y less or equal X >= Y greater or equal