Tutorial Understanding the Complexity of B Animation
We assume that you grasped the way that ProB setups up the initial states of a B machine as outlined in Tutorial Setup Phases.
In this lesson, we examine the complexity of animation of B models in general, how ProB solves this problem and what the ramification for users are.
Undecidability
In general, animation of a B model is undecidable. I.e., it is undecidable whether a solution to the PROPERTIES can be found, whether a valid INITIALISATION exists and whether an operation can be applied.
For example, the following B machine encodes Goldbach's conjecture (that every even number greater than 2 is a Goldbach number, i.e., it can be expressed as the sum of two primes):
MACHINE Goldbach
DEFINITIONS
prime(x) == x>1 & !y.(y:NATURAL & y>1 & y<x => x mod y /= 0)
OPERATIONS
GoldbachNumber(x,p1,p2) = SELECT x:NATURAL & x mod 2 = 0 & x>2 &
p1<x & p2<x & p1<=p2 & prime(p1) & prime(p2) & x = p1+p2 THEN
skip
END;
NotGoldbachNumber(x) = SELECT x:NATURAL & x mod 2 = 0 & x>2 &
!(p1,p2).(p1<x & p2<x & p1<=p2 & prime(p1) & prime(p2) => x /= p1+p2) THEN
skip
END
END
If the conjecture is true, then the operation NotGoldbachNumber is disabled; if the conjecture is false then it is enabled.
How does ProB overcome undecidability. First, it will enumerate integer variables only between MININT and MAXINT (unless the machine itself fixes the value to be outside of that range).
Hence, ProB will look for solutions to the parameter x of NotGoldbachNumber only until MAXINT. Hence, if we set MAXINT to 16 (adding a definiton SET_PREF_MAXINT == 16) we get the following picture after executing the INITIALISATION:
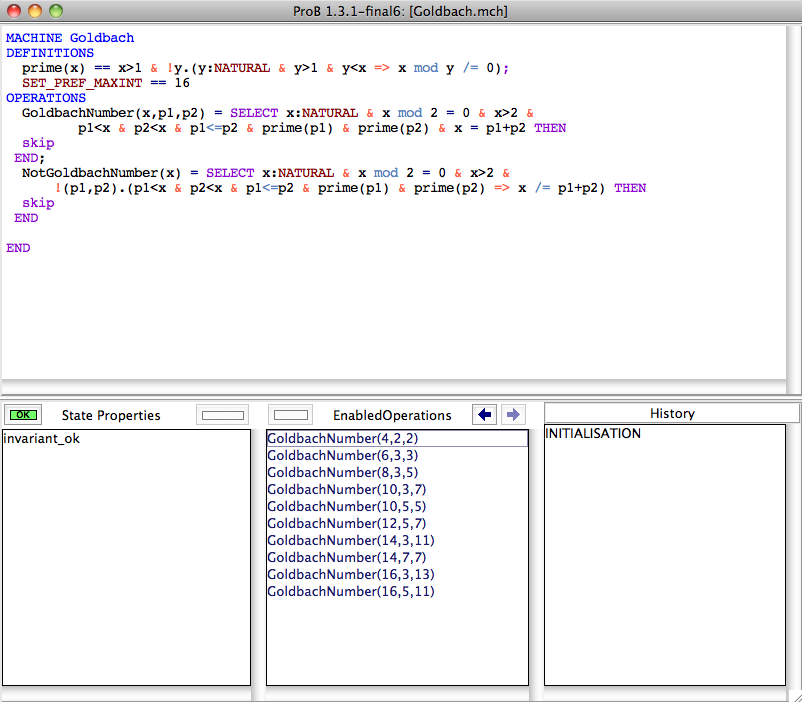
We can see that 10 can be expressed as the sum 5+5 or 3+7. At least until 16, Goldbach's conjecture is confirmed, as NotGoldbachNumber is disabled.
Note, that this restriction (of enumerating only between MININT and MAXINT) means that ProB is in general incomplete and sometimes unsound when using mathematical integers. We recommend, using the implementable integers only (INT, NAT, NAT1). In future, we plan to integrate an interval analysis into ProB which to highlight predicates over mathematical integers which are potentially problematic.
The mathematical integers are, however, not the only source of undecidability. Another source stems from the deferred sets. Indeed, the size of those sets maybe unknown and they may even be infinite. To overcome this issue, ProB requires to fix the cardinality of every deferred set to a finite number before animation (see also Understanding the ProB Setup Phases on how you can control the cardinality of the deferred sets).
Complexity of Animation
However, having addressed the undecidability issue still leaves open the problem of complexity. Indeed, even for finite sets and implementable integers, the animation task can be arbitrarily complex. Take for example the following predicate, declaring rr to be a binary relation over -3..3:
rr : (-3..3) <-> (-3..3)
This predicate could be part of a precondition of an operation. In order to find possible enablings of the operation the possible values for rr need to be examined. Even if ProB did enumerate 100,000 candidate solutions for rr per second, it would take over 178 years to check all solutions for rr. Indeed, there are 49 possible pairs of values between -3 and 3 and hence 2^49 = 562,949,953,421,312 binary relations over -3..3.
The following table shows how the size of a deferred set S influences the number of subsets, partial functions and relations over S:
| card(S) | sub:POW(S) | pf:S+->S | rel: S<->S |
|---|---|---|---|
| 1 | 2 | 2 | 2 |
| 2 | 4 | 9 | 16 |
| 3 | 8 | 64 | 512 |
| 4 | 16 | 624 | 65,536 |
| 5 | 32 | 7,776 | 33,554,432 |
| 6 | 64 | 117,649 | 6.87e+10 |
| 7 | 128 | 2,097,152 | 5.63e+14 |
| 8 | 256 | 43,046,721 | 1.85e+19 |
| 9 | 512 | 1,000,000,000 | 2.42e+24 |
(Note that the age of the universe is about 4e+17 seconds and 4e+26 nanoseconds.)
In order to make a B model amenable to animation, we have three options:
- use small cardinalities for the deferred sets and avoid using overly complicated datastructures (e.g., relations over relations)
- ensure that ProB does not have to enumerate variables with complicated types, by providing concrete values (e.g., in the form of an equality rel = {1|->2, 2|->3, 3|->1}
- hope that the constraint solver of ProB will be able to find a solution.