Cheryl's Birthday
This Puzzle is a variation of another Puzzle (Sum and Product) and has been described in a New York Times article.
Here is a first solution in B, where the text of the puzzle has been integrated as comments. There are almost certainly more elegant encodings of the problem in B.
MACHINE CherylsBirthday
/* A simplified version of the SumProduct Puzzle taken from
http://www.nytimes.com/2015/04/15/science/a-math-problem-from-singapore-goes-viral-when-is-cheryls-birthday.html
*/
DEFINITIONS
DontKnowFromDay(PossDates,KDay) == card(PossDates~[{KDay}]) > 1;
KnowFromDay(PossDates,KDay) == card(PossDates~[{KDay}]) = 1
CONSTANTS Month, Day, PD, PD2
PROPERTIES
/* Albert and Bernard just met Cheryl. “When’s your birthday?” Albert asked Cheryl.*/
Month:STRING & Day:NATURAL1 &
/* Cheryl thought a second and said, “I’m not going to tell you, but I’ll give you some clues.” She wrote down a list of 10 dates: */
PD = {("aug"|->14),("aug"|->15),("aug"|->17),
("july"|->14),("july"|->16),("june"|->17),("june"|->18),
("may"|->15),("may"|->16),("may"|->19)}
&
/*
Then Cheryl whispered in Albert’s ear the month — and only the month — of her birthday.
To Bernard, she whispered the day, and only the day.
*/
Month : dom(PD) &
Day : ran(PD) &
Month|->Day : PD &
/* Albert: I don’t know when your birthday is, */
card(PD[{Month}]) > 1 &
/* but I know Bernard doesn’t know, either. */
!x.(x:PD[{Month}] => DontKnowFromDay(PD,x) ) &
/* Bernard: I didn’t know originally, */
DontKnowFromDay(PD,Day) &
/* but now I do. */
PD2 = {m,d| (m|->d):PD & !x.(x:PD[{m}] => DontKnowFromDay(PD,x) ) } &
KnowFromDay(PD2,Day) &
/* Albert: Well, now I know, too! */
card({d|Month|->d : PD2 & KnowFromDay(PD2,d)})=1
ASSERTIONS /* single solution found by ProB in 20-30 ms */
Month = "july";
Day = 16
END
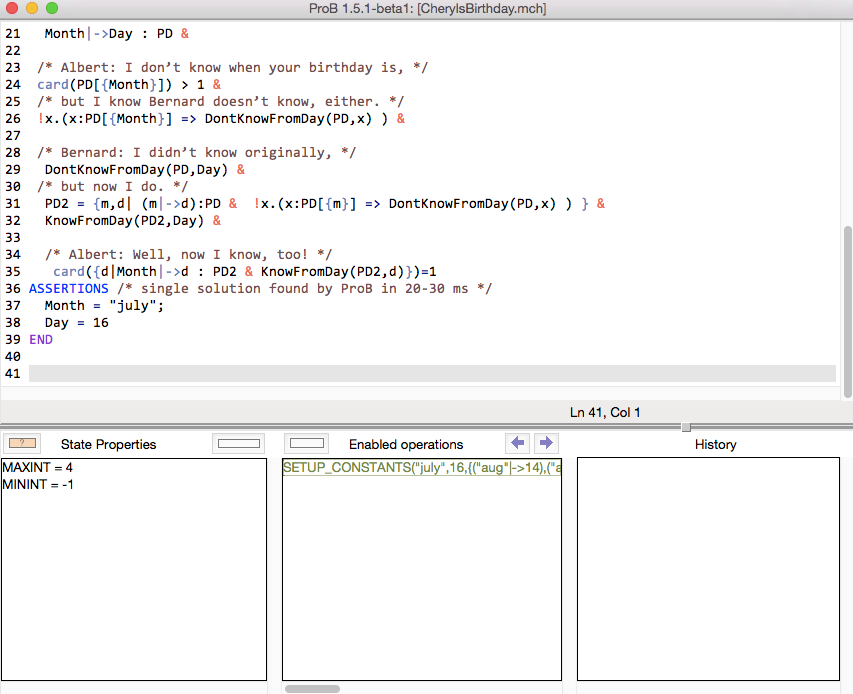
When loading this B machine in ProB, you will see that there is only a single solution (solving time 20-30 ms) : Month = "july" and Day = 16.
Here is a screenshot of ProB Tcl/Tk after loading the model.
Using an enumerated set
It is possible to use an enumerated set for the Months. One simply has to add
SETS MONTHS = {may, june, july, aug, sep}
and then change the definition of the possible dates:
PD = {(aug|->14), (aug|->15), (aug|->17),
(july|->14),(july|->16),(june|->17),
(june|->18),
(may|->15),(may|->16),(may|->19)}
and also "july" in the ASSERTIONS clause into july. This makes constraint solving via ProB marginally faster.