Tutorial Various Optimizations
The ordinary model checker of ProB enables the user to verify automatically whether a B model contains any errors such as deadlocks and invariant violations. The search for errors is performed by a graph traversal algorithm exploring the state space until an error state has been found or all states of the model have been explored. The runtime of the model checker is mostly determined by the number of states of the model being analyzed and thus model checking is generally limited by the size of the state space of the model. The problem is also known as the state space explosion problem.
To combat the state space explosion problem two advantageous techniques, partial guard evaluation and partial order reduction, for the ordinary model checker of ProB have been implemented for model checking practically B and Event-B models with huge state spaces. This tutorial describes how one can apply model checking using the optimizations and additionally gives hints when it is recommendable to use these optimizations.
Partial Order Reduction
Partial order reduction (POR) is a method proposed for combating the state space explosion problem by means of state space reduction. The technique takes advantage of the commutativity of concurrently executed actions. The reduction relies on selecting a subset of all enabled actions in each reachable state of the state space aiming in this way to reduce the number of possible orderings of actions. Basically, the idea is to check only a fragment of the original state space that is sufficient for checking the given property.
Take, for example, the following B machine:
MACHINE Example VARIABLES x,y,z INVARIANT x:INT & y:INT & z:INT INITIALISATION x,y,z:=0,0,0 OPERATIONS IncX = PRE x=0 THEN x:= x+1 END; IncY = PRE y=0 THEN y:= y+1 END; IncZ = PRE z=0 THEN z:= z+1 END END
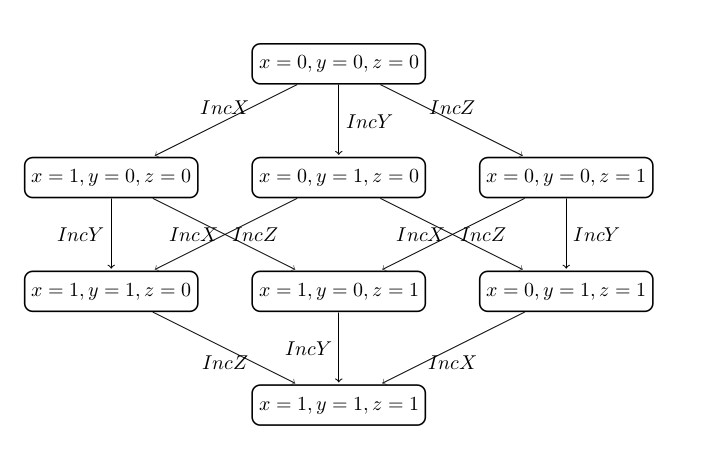
The machine has a deadlock state. The deadlock state will be reached by executing each of the operations IncX, IncY, and IncZ. The order of executing the operations is irrelevant with respect to reaching the deadlock state. This can be seen, for example, by observing the full state space of the machine:
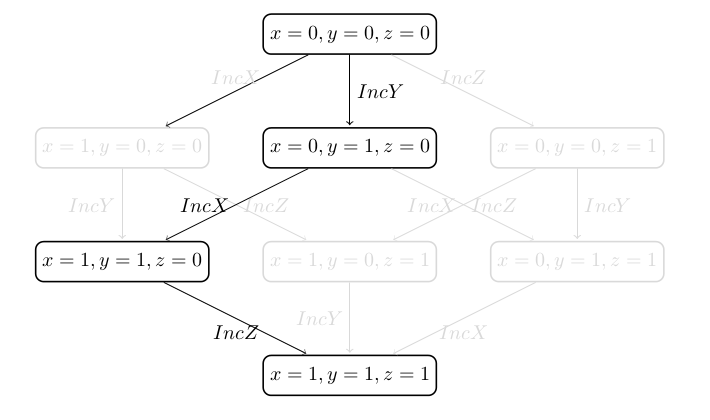
Since the order in which the operations are executed is not relevant for discovering the deadlock state it is sufficient to examine only one of the six paths that start in the initial state and reach the deadlock. Thus, for the machine it is enough to analyze only one arbitrary order of the events in order to detect the deadlock:
Using this observation the ordinary model checker of ProB has been extended to check a model formalized in B or Event-B using partial order reduction. More information about the implementation of POR in ProB and the theoretical background of POR can be read here. Our implementation of POR uses the ample set theory [1].
For enabling the POR optimization for the model checker in Tcl/Tk interface of ProB a new check box “Partial Order Reduction” has been added to the “Model Checker” menu. Note that the option shows up only when the user mode is set to “Normal” (see Preferences → User Mode in the menu bar). The POR optimization can be enabled for model checking B and Event-B models with the command line version of ProB by setting the 'por' preference to the value 'ample_sets'. For example, the machine Example can be checked for deadlock and invariant violations using the POR optimization with the command line version of ProB as follows:
$ probcli Example.mch -mc 10000 -p por ample_sets ********* DETERMINE ACTION DEPENDENCIES AND ENABLE GRAPH ************* ********** FINISHED ANALYSIS ************* Analysis Checking Time: 10 ms. ALL OPERATIONS COVERED found_error(deadlock,3) finding_trace_from_to(root) Model Checking Time: 40 ms (100 ms walltime) States analysed: 3 Transitions fired: 4 *** COUNTER EXAMPLE FOUND *** deadlock *** TRACE: 1: INITIALISATION(0,0,0): 2: IncZ: 3: IncX: 4: IncY: ! *** error occurred *** ! deadlock
As a result the deadlock has been discovered by exploring in total 3 states using the Mixed DF/BF search strategy. Model checking the machine without using POR will possibly explore more states until it finds out the deadlock state (recall that the full state space of Example.mch consists of 8 states). Note that the POR algorithm can be applied to all exploration strategies (DF, BF, and Mixed DF/BF) of the ordinary model checker of ProB.
The reduction of the state space takes effect by choosing a subset of the set of all enabled transitions in the currently explored state. The set of all enabled transitions in some state s is usually denoted by enabled(s) and the subset of the transitions chosen to be executed in s is denoted by ample(s). The set ample(s) we call an ample set for state s. Each ample set should satisfy certain conditions (the ample set requirements) in order to guarantee that the reduction of the state space is sound in regard to the property being checked on the model. In fact, there are four conditions that each ample set should satisfy:
- (A 1) ample(s) = {} <=> enabled(s) = {}
- (A 2) Along every finite execution in the original state space starting in s, an event dependent on ample(s) cannot appear before some event from ample(s) is executed
- (A 3) If ample(s) is a proper set of enabled(s), then each transition in ample(s) is a stutter transition.
- (A 4) For any cycle C in the reduced state space, if a state in C has an enabled event e, then there exists a state s in C such that e is an element of ample(s).
To guarantee that all deadlocks in the full state space are also preserved in the reduced state space it is sufficient when all computed ample sets satisfy just the first two conditions <citation needed>. This suggests that in some cases, when we check for deadlock freedom only, the reduction of the state space may be more effective if each ample set satisfies only the first two ample set requirements. That is, model checking with POR usually tends to yield more state space reduction when checking a model for deadlock freedom only than checking it for invariant violations or simultaneously for deadlock freedom and invariant violations. (The reduction algorithm of ProB has been adapted to this fact.) For this reason, keep in mind to disable the “Invariant Violations” option if it is intended to check a B or Event-B model just for deadlocks using the POR optimization as the potential for more significant reduction of the state space is higher.
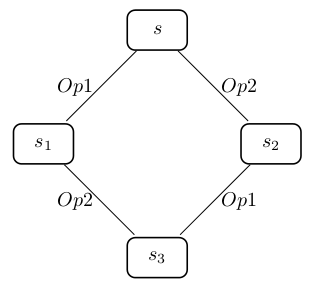
The reduction algorithm makes use of the independence of transitions. Two transitions Op1 and Op2 are called independent if for each state s where both are enabled we have the following situation:
Let us assume that the transitions Op1 and Op2 in Figure above constitute the executions of two deterministic operations of a B machine. Then we can say that the operations Op1 and Op2 are independent, when they cannot disable one other and additionally both possible orders of execution of the operations <Op1,Op2> and <Op2,Op1> starting in some state s reach the same state s3. If two transitions are not independent, then both are denoted as dependent.
To find out whether two operations are independent one can analyze the syntactical structure of both operations. If each of the operations modifies variables of the machine not read by the other one and if both operations modify different variables, then these operations are considered to be independent. Besides performing only a syntactical analysis, we use also the constraint-based facilities of ProB to determine more exact relations between the operations. The reason for those extra analyzes lies in the high potential for significant reduction of the state space when the degree of independence of the checked B model is high.
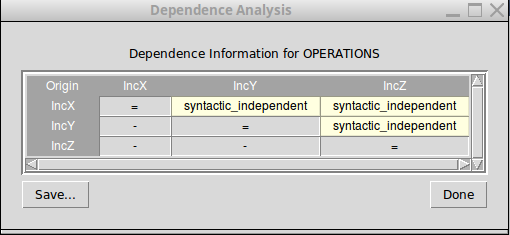
Thus, if we have a great amount of independent operations for some B machine, then we have a great potential for significant state space reduction. The results of the analyses for determining the independence of operations for a particular B machine, which are used by the reduction algorithm for computing the ample sets, can be viewed in the menu bar of the Tcl/Tk interface of ProB: “Verify → Enabling Analysis → Dependence Analysis (Table)”. For example, the dependency table for the model 'Example.mch' looks as follows:
The results in the dependency table for a pair of operations Op1 and Op2 have the following meanings:
- syntactic_independent : Op1 and Op2 are syntactically independent; both events write different variables and no one of the events can write a variable which is read by the other one
- independent : one of the events or both events write variables read only in the guard of the other one, though the events cannot disable each other
- dependent : the events are not independent
- race_dependent : Op1 and Op2 have write variables in common
- - : the dependency relation is symmetric, see (Op2,Op1) result
- = : Op1 and Op2 represent the same event
To sum up, in order to take an advantage of POR the model being checked should have many independent operations that are concurrently executed. In other words, the magnitude of reduction depends on the coupling between the operations in the B model. Thus, it is recommended to use the reduced search when the analyzed model has comparatively many independent operations that are concurrently executed in order to gain from the improvement by the reduction technique. For example, if a B model has no pair of independent operations or all independent operations are not executed concurrently, i.e. two independent operations are never simultaneously enabled, then no reductions of the state space will be performed using the reduced search algorithm.
The reduction algorithm has been evaluated on various B and Event-B models. The evaluation can be obtained here.
Partial Guard Evaluation
When checking for consistency a B model the ProB model checker traverses the state space of the model beginning in some of the initial states and checks for errors each state, which it encounters. The ProB model checker explores the state space of the B machine by applying all operations of the machine to the current state. As a result, the successor states of the state are determined. The exploration of the state space continues until all possible states are explored or an error state is found.
When a state, say s, is processed the following steps are consequently performed:
- Checking s for errors like invariant violation, assertion violation, and deadlock;
- Applying the machine's operations to s.
The second step is carried out in case no error was discovered previously (in step 1.). When step 2. is performed in some state s all operations of the checked B model are tested for being enabled in s and the substitutions of each enabled operation are performed at s.
The effort of checking a state amounts thus to checking the state for errors (testing for invariant violation, assertion violations etc.) plus the computation of the successors. There is some redundancy in testing all operations' guards in each state, as usually there are operations that are disabled in the states being explored. Especially, when the model checker has to check exhaustively B models with large state spaces the effort of testing the guard of each operation in every state may be huge. Thus, an optimization may be considered by means of decreasing the state space exploration complexity by trying to reduce the overall number of guard tests via skipping the guard evaluations of operations known to be disabled in some states.
One can determine a set of disabled operations in a state s by considering, for example, the incoming transitions of s. During the observation of the incoming transitions we examine how the operations represented by the incoming transitions may influence other operations. If, for example, operation ‘A’ surely disables operation ‘B’ we can assume that ‘B’ is disabled at each state having ‘A’ as incoming transition. This and other such relations can be used to optimize the ProB model checker for exhaustively checking B models. This type of relations we will also call enabling relations.
Enabling relations between operations reveal how operations of a given B model could influence each other with regard to enabledness. In other words, we are interested in the effect of executing one operation Op1 on the status of the guard of another operation Op2 for each pair of operations (Op1,Op2) of the underlying B model. The effect of an operation Op1 can affect the guard of another operation Op2 in various ways:
- Op1 enables Op2, or
- Op1 disables Op2, or
- Op1 keeps Op2 enabled respectively disabled;
This enabling relation of two operations we can illustrate, for example, as follows:
where the green boxes denote that the evaluation of the guard of Op2 is true, whereas the red boxes indicate that the evaluation of the guard of Op2 is false.
The model checker optimization, partial guard evaluation, makes use of such kind of relations. The enabling relations are determined by means of syntactic and constraint-based analyses. In particular, we concentrate on three kinds of enabling relations:
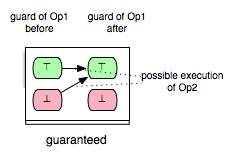
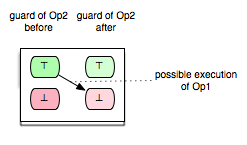
Op2 is always enabled after the execution of Op1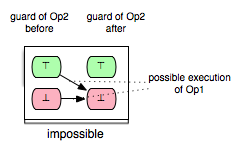
Op2 is impossible to be enabled after the execution of Op1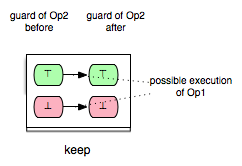
Op2 keeps Op1 enabled respectively disabled
Consider the B machine below modelling an algorithm for mutual exclusion with semaphores for two concurrent processes and . Each process has been simplified to perform three types of actions: request (for entering in the critical section), enter (entering the critical section), and release (exiting the critical section).
MACHINE MutualExclusion
SETS
STATE={non_critical,waiting,critical}
VARIABLES
p1,p2,y
INVARIANT
y : 0 .. 1 & not(p1 = critical & p2 = critical)
INITIALISATION
p1, p2, y := non_critical, non_critical, 1
OPERATIONS
Req1 = PRE p1 = non_critical THEN p1 := waiting END;
Enter1 = PRE p1 = waiting & y = 1 THEN p1 := critical || y := 0 END;
Rel1 = PRE p1 = critical THEN p1 := non_critical || y := 1 END;
Req2 = PRE p2 = non_critical THEN p2 := waiting END;
Enter2 = PRE p2 = waiting & y = 1 THEN p2 := critical || y := 0 END;
Rel2 = PRE p2 = critical THEN p2 := non_critical || y := 1 END
END
Each process has three possible states that are denoted by the constants (the state in which performs noncritical actions), (the state in which waits to enter the critical section), and (representing the state in which is in the critical section). Both processes share the binary semaphore y, where y=1 indicates that the semaphore is free and y=0 that the semaphore is currently processed by one of the processes.
In the B machine the operations `Req1`, `Enter1` and `Rel1` represent the actions request, enter and release of , respectively. Analogously, the operations `Req2`, `Enter2` and `Rel2` represent the actions request, enter and release of , respectively. The requirement always at most one process is in its critical section guaranteeing the mutual exclusion property is stated in the invariant of the machine by means of the predicate not(p1 = crit1 & p2 = crit2).
To verify that the B machine satisfy the mutual exclusion property and has no deadlock state one can use the ProB model checker. This will explicitly generate all possible states of the machine and check whether there is any state that is a deadlock state or that violates the invariant. As a result, eight states will be generated and checked, the machine is consistent with respect to the invariant and has no deadlock state. By the exhaustive search for error states the model checker will test by exploring the state space each guard of the machine’s operations for being enabling in the currently processed state. That is, while exploring the state space of the machine 48 guard tests (8 states 6 operations) will be performed in order to explore the entire state space.
| Origin | Req1 | Enter1 | Rel1 | Req2 | Enter2 | Rel2 |
| Req1 | impossible | enable | impossible | keep | keep | keep |
| Enter1 | impossible | impossible | guaranteed | keep | impossible | keep |
| Rel1 | guaranteed | impossible | impossible | keep | enable | keep |
| Req2 | keep | keep | keep | impossible | enable | keep |
| Enter2 | keep | impossible | keep | impossible | impossible | guaranteed |
| Rel2 | keep | enable | keep | guaranteed | impossible | impossible |
References
- ↑ E.M. Clarke, O. Grumberg, M. Minea, and D. Peled: State Space Reduction using Partial Order Reduction. STTT '98, 3, pages 279-287