Apples and Oranges (Apple Interview Question)

This puzzle is apparently an Interview question at Apple. Quoting from [1] we have the following information:

• (1) There are three boxes, one contains only apples, one contains only oranges, and one contains both apples and oranges.
• (2) The boxes have been incorrectly labeled such that no label identifies the actual contents of the box it labels.
• (3) Opening just one box, and without looking in the box, you take out one piece of fruit.
• (4) By looking at the fruit, how can you immediately label all of the boxes correctly?

Here is one encoding of this puzzle in B:

MACHINE ApplesOranges
SETS
 Fruit={apple,orange}; // possible content for the boxes
 Label={A,O,Both} // labels for the boxes
CONSTANTS a,o,b,  // a,o,b are the three boxes
          Take,  // which box should we open (the label of that box)
          DecisionFunction // given the fruit we pick from Take: what are the contents of the boxes labeled A,O,Both
PROPERTIES
  a = {apple} & o={orange} & b={apple,orange} // (1)
  &
  Take : Label //3 
  &
  DecisionFunction : Fruit --> (Label >->> {a,o,b}) & //4
  !label. ( // the decision function has to work for all allowed labelings
  ( label : {a,o,b} >->> Label &
    label(a) /= A & label(o) /= O & label(b) /= Both // (2)
  )
   =>
  !f.(f: label~(Take) 
      => DecisionFunction(f)=label~ // the function should tell us what is behind label A,O,Both
     )
  )
END

We have abstracted the box of apples a by the set containing apple. Ditto for o and b, which are abstracted by {orange}</tt} and {apple,orange} respectively.

Note: you need a recent version of ProB 1.5.1-beta3 or newer to load the above model with its one-line comments. If you have an older version of ProB, simply use the normal comments /* ... */.

Loading this model with ProB gives you just one solution (after less than 10 ms):

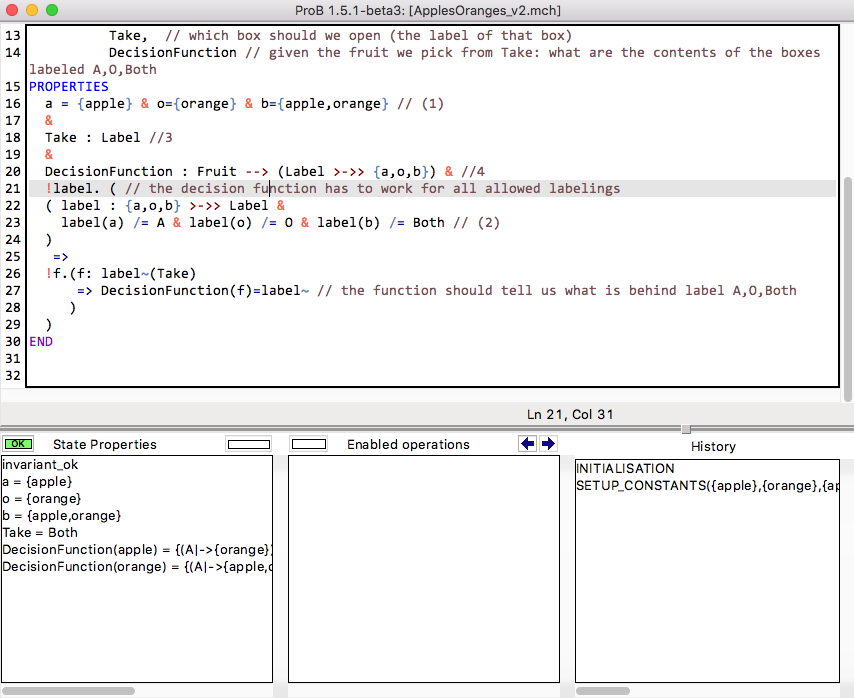
As we can see, the only solution is to open the box labelled with "Both". We can inspect the decision function by using the B REPL (e.g., double click on the State Properties pane to open it):

>>>> DecisionFunction(apple)
  {(A|->{orange}),(O|->{apple,orange}),(Both|->{apple})}
  
>>>> DecisionFunction(orange)
  {(A|->{apple,orange}),(O|->{apple}),(Both|->{orange})}