Tutorial Model Checking, Proof and CBC: Difference between revisions

We assume that you have completed Tutorial Complete Model Checking.

Let us examine the following B machine:

MACHINE DoubleCounter
VARIABLES counter
INVARIANT
 counter:NATURAL & counter<=128
INITIALISATION counter:=8
OPERATIONS
  Double = PRE counter<100 THEN counter := 2*counter END;
  Halve = BEGIN counter := counter/2 END
END

Now click the "Model Check" button. After a short while, ProB will give you the following message:

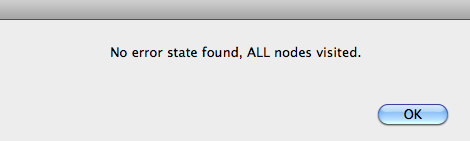
Is this model correct? As you will see, this depends on your point of view.

State Space

If you look purely at the state space of the machine (choose the View State Space command in the Animate menu) you get the following picture:

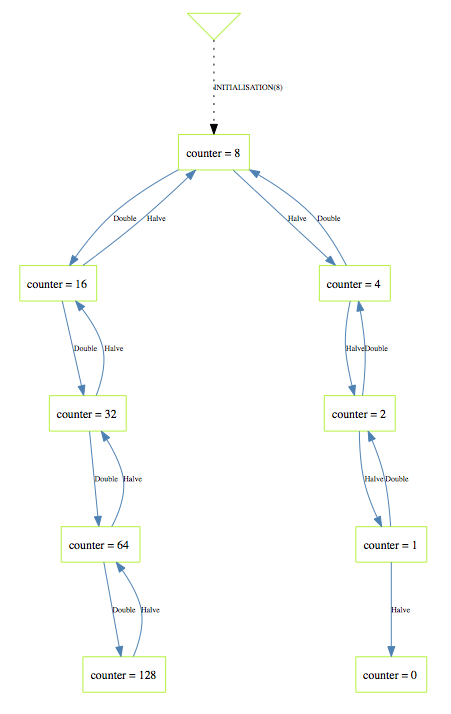
Indeed, all reachable states are correct, in the sense that the invariant counter:NATURAL & counter<=128 holds for all of those states.

However, you will not be able to prove the system correct using AtelierB or Rodin.

Constraint Based Checking (CBC) for the Invariant

In addition to model checking, ProB also offers constraint-based checking (CBC), which is particularly useful when used in conjunction with proof. This will give us the clue as to why the above machine cannot be proven correct, and why it can also be viewed as incorrect.

Before proceeding, please ensure that you have either set the CLPFD preference to TRUE or have set the MAXINT preference to at least 130. This can be set by going to the "Animation Preferences" command in the Preferences menu or by adding for example the following to your file and then reloading it:

DEFINITIONS SET_PREF_CLPFD == TRUE

Let us choose the "Check Invariant Preservation for Operation" command inside the "Constraint Based Checking" submenu:

(You This will report an invariant violation and transport you to the following state:

As you can see, the Counter has the value 130, which clearly violates the invariant counter<=128. However, no value in the state space above did have this value for Counter. So how did we reach this error state? By pressing the left arrow in the "EnabledOperations" pane you will see the previous state that ProB has computed:

Now, while this state does not appear in the state space above either. However, this time this state does satisfy the invariant. Thus, if we ignore the initialisation and just look at the INVARIANT counter:NATURAL & counter<=128 as describing all possible states, then the machine is indeed erroneous: the operation Double lead us outside of the safe states. The operation Halve on the other hand is correct: for every possible state satisfying the INVARIANT the resulting successor state will also satisfy the INVARIANT.

If you look purely at the state space of the machine (choose the View State Space command in the Animate menu) you get the following picture:

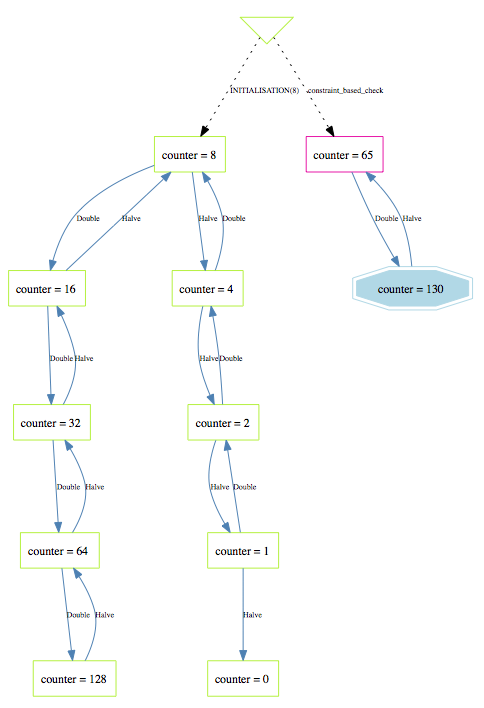
As you can see the constraint-based checker has transported us into the state with Counter=65, which is not reachable from the initial state of the system. However, as we have said, it does satisfy the invariant and as such the machine cannot be proven using the B provers. Indeed, the proof obligation in classical B for an operation with precondition P and body S is:

I & P => [S] I

In other words, for any state which satisfies the invariant I and the precondition P, the operation must preserve the invariant; not just for the states reachable from the initialisation.