Tutorial Understanding ProB's Constraint Solver: Difference between revisions
No edit summary |
No edit summary |
||
| Line 155: | Line 155: | ||
You can now type A followed by RETURN. This will typically raise an error message, which you can dismiss. Afterwards, you should be able to continue working. | You can now type A followed by RETURN. This will typically raise an error message, which you can dismiss. Afterwards, you should be able to continue working. | ||
Finally, one can control the time after which a timeout will trigger using the preference "Time out for computing enabled transitions (in ms)" in the Animation Preferences. You can also control it using a definition for<tt>SET_PREF_TIME_OUT</tt> in the DEFINITIONS clause. | Finally, one can control the time after which a timeout will trigger using the preference "Time out for computing enabled transitions (in ms)" in the Animation Preferences. You can also control it using a definition for <tt>SET_PREF_TIME_OUT</tt> in the DEFINITIONS clause. | ||
Revision as of 15:04, 19 January 2010
We assume that you grasped the way that ProB setups up the initial states of a B machine as outlined in Tutorial Setup Phases, and have understood why animation is difficult as outlined in Tutorial Understanding the Complexity of B Animation.
First, it is important to understand that as of version 1.3, ProB uses two representations for sets and relations:
- a classical list representation
- a representation using AVL-trees.
The second representation allows ProB to deal with larger sets and relations (starting at around 100,000 elements performance will start to slow down). However, this representation can only be used if the constraint solver knows exactly all elements of a set or relation. The list representation will be used if only part of the set or relation is known.
To give an idea about the performance related to the new AVL-based representation, take the substitution
numbers := numbers - ran(%n.(n:cur..limit/cur|cur*n))
- For limit=10,000 this takes 0.2 seconds (on a 2008 laptop); with the list representation this operation ran out of memory after 2 minutes in ProB 1.2.x.
- For limit=100,000 this takes 2.1 seconds. (An encoding of this problem in Kodkod took 363 seconds on the same hardware.)
- For limit=1,000,000 this takes about 21.9 seconds.
For example, if the PROPERTIES contains the following predicates
- x = {1,2}
- y = {1|-2, 3|->4, 4|->5}
- a = 1 & b=2 & d = {a|-b}
then all values will be fully known and the new AVL-based representation will be used. However, for example for
- card(x) = 2 & dom(x) = {1,2}
we would only have partial information about x (which the constraint solver will encode using the list [1|->_, 2|->_] where the underscore marks as of yet unknown bits.
Basically, the ProB constraint solver works as follows:
- while interpreting the predicates, it will first try to "execute" predicates (or sub-predicates) which result in information which can be stored in AVL-form
- after having interpreted the whole predicate, it will then perform deterministic propagation
- only after all deterministic propagation has been performed, will the constraint solver start enumerating possibilities. For this it maintains a priority queue of enumerations and choice points.
The priority is a rough estimate of the number of possible solutions; predicates with the lowest estimate will be "executed" first.
The following picture provides a very rough picture of this process:
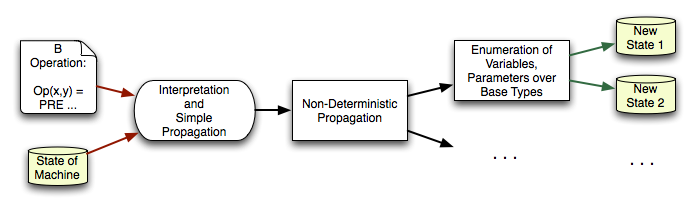
A simple example
Let us use the following B machine as starting point:
MACHINE Propagation
CONSTANTS low,up,f,fi,invert
PROPERTIES
f:low..up --> 0..1 &
invert: 0..1 --> 0..1 &
fi = (f ; invert) &
invert = {0|->1,1|->0} &
low = 0 & up = 3 &
f = {0 |-> 1, 1|->1, 2|->0, 3|->1}
VARIABLES xx
INVARIANT
xx:low..up
INITIALISATION xx:=low
OPERATIONS
val <-- Sense = BEGIN val := f(xx) END;
Inc = IF xx<up THEN xx := xx+1 ELSE xx := low END
END
After loading the file, we get offered one possible way to setup the constants:
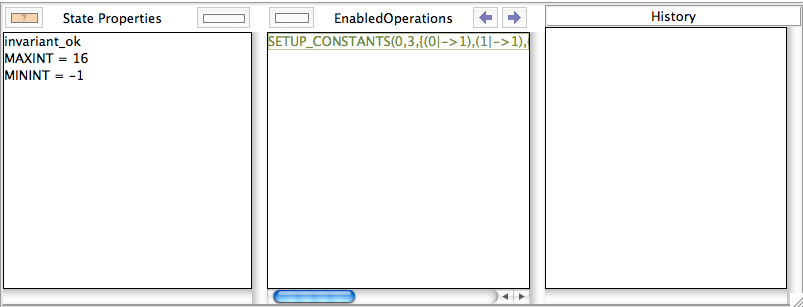
In this case, ProB performed no enumeration at all. It could immediately determine the values of all constants. We can inspect the behaviour of the constraint solver by choosing "Advanced Preferences..." in the Preferences menu and the turning the "Provide various tracing information on the terminal/console" on. If we now reopen the machine, the following information will be printed (amongst others) on the console:
...
% checking_properties
====> low = 0
-->> low
val/1: int(0)
====> up = 3
-->> up
val/1: int(3)
====> invert = {0 |-> 1,1 |-> 0}
-->> invert
val/1: AVL.size=2
====> f = {0 |-> 1,1 |-> 1,2 |-> 0,3 |-> 1}
-->> f
val/1: AVL.size=4
====> f : low .. up --> 0 .. 1
====> invert : 0 .. 1 --> 0 .. 1
====> fi = f ; invert
-->> fi
val/1: AVL.size=4
-->> SUCCESS; all constants valued
% start_enumerating_constants
% grounding_wait_flags_for_constants(wfx(_57893,_66619,_56937))
% found_enumeration_of_constants(10)
...
The arrow -->> shows us when an AVL-representation was found for a constant. The ====> tells us when a predicate is interpreted. You can also see that all constants have been valued before enumeration was started. You can also see that ProB does not treat the predicates in the same order as you have typed them in the PROPERTIES clause: indeed, ProB sorts the properties (e.g., moving equalities earlier) before starting the interpretation.
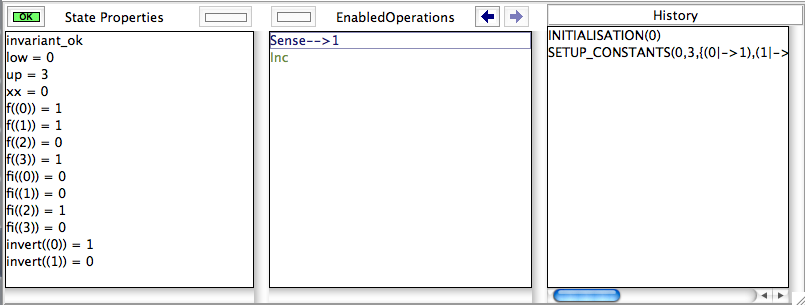
After selecting SETUP_CONSTANTS and INITIALISATION, we obtain the following state, and we can ensure ourselves that the values found for f and fi are correct (by looking at the "State Properties" pane):
Complicating the Example
To make the example more challenging, let us increase up to 100 and remove the equality for f. In other words, the PROPERTIES will now look like this:
f:low..up --> 0..1 &
invert: 0..1 --> 0..1 &
fi = (f ; invert) &
invert = {0|->1,1|->0} &
low = 0 & up = 100
Saviang and reopening the machine, results in the following picture:
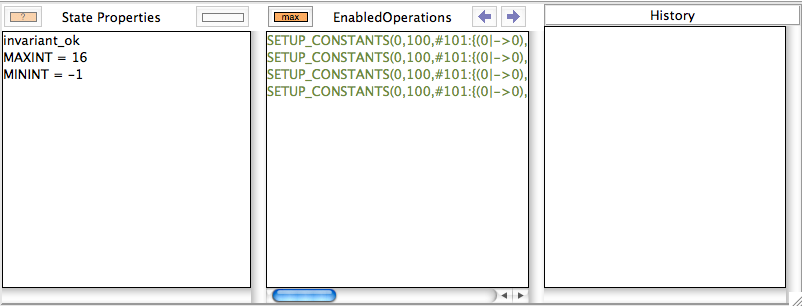
You can see that ProB had to problem with this machine. Still, one may wonder why it only proposes four solutions for the constants. Indeed, there should be 2^101 = 2.54e+30 different solutions (over 2 thousand billion billion billion solutions). In fact, as quite often there are a lot of solutions for the constants, ProB (luckily) does not compute all of them. Indeed, there is a cut-off point after which it will no longer search for more solutions. In this case, the orange button "max" appears in the "Enabled Operatoins" pane. The cut-off itself is controlled by a preference. You can either
- change the preference "Max Number of Initialisations Computed" in the "Animation Preferences", or
- add a definition SET_PREF_MAX_INITIALISATIONS == xxx, where xxx is the maximum number of initialisations or possible ways to value the constants that ProB should compute.
There is a similar preference to control how many solutions are found for ways to execute an operation (SET_PREF_MAX_OPERATIONS).
One may wonder what happens if there are no solutions. Will not ProB have to examine all of these solutions? The answer is: sometimes yes. Let us add the predicate f=fi to the PROPERTIES, which are now unsatisfiable. If we save and reopen the machine, we get the following picture:
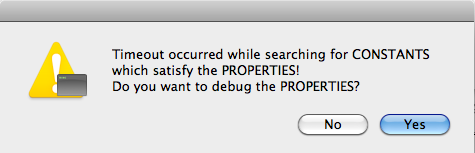
If we answer yes, the Properties will be debugged by adding conjuncts one-by-one. We obtain the following:
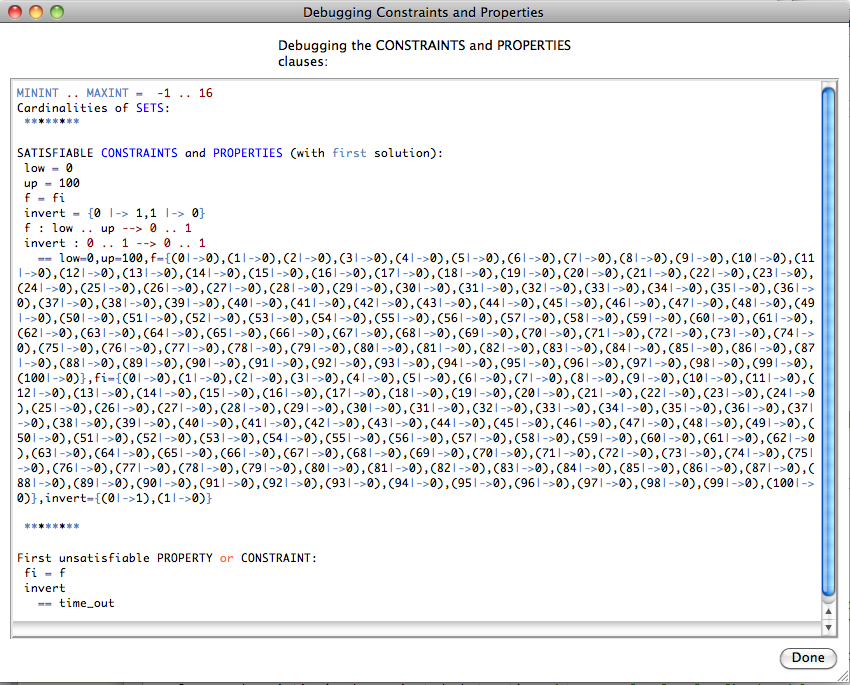
This will hopefully help us pinpoint the error in our properties. See Tutorial Troubleshooting the Setup for more ways to locate problems in the properties. After clicking Done, we get the following; observe the orange timeout button in the "State Properties" pane:
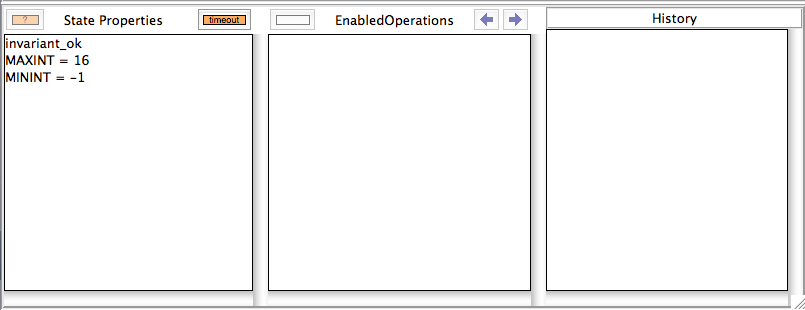
Note that one can click on the orange Timeout button: this will offer us the option to try to find solutions without a timeout. You should use this option with care: it can lock up your computer for a long time. You should be able to stop the computation by selecting ProB's terminal window and hitting CONTROL-C. Hopefully, the following message will appear in the terminal:
^CProlog interruption (h for help)?
You can now type A followed by RETURN. This will typically raise an error message, which you can dismiss. Afterwards, you should be able to continue working.
Finally, one can control the time after which a timeout will trigger using the preference "Time out for computing enabled transitions (in ms)" in the Animation Preferences. You can also control it using a definition for SET_PREF_TIME_OUT in the DEFINITIONS clause.