Checking CSP Assertions: Difference between revisions
| Line 40: | Line 40: | ||
<tt>assert P |= LTL: “f”</tt> | <tt>assert P |= LTL: “f”</tt> | ||
Note that ''f'' must be | Note that ''f'' must be placed between quotes and that the satisfaction relation |= is immediately followed by `LTL:`. ProB supports LTL<sup>[e]</sup>, an extended version of LTL which provides additionally support for making propositions on transitions. The following LTL<sup>[e]</sup> syntax for CSP-M specifications can be outlined by the following rules: | ||
* Atomic propositions: | * Atomic propositions: | ||
| Line 60: | Line 60: | ||
** `WF(evt)` or `wf(evt)`: weak fairness, where `evt` is an event | ** `WF(evt)` or `wf(evt)`: weak fairness, where `evt` is an event | ||
** `SF(evt)` or `sf(evt)`: strong fairness, where `evt` is an event | ** `SF(evt)` or `sf(evt)`: strong fairness, where `evt` is an event | ||
** `WEF` and `SEF` for checking LTL[e] formulae on executions that are strongly and weakly fair with respect to all events, respectively | ** `WEF` and `SEF` for checking LTL<sup>[e]</sup> formulae on executions that are strongly and weakly fair with respect to all events, respectively | ||
An LTL<sup>[e]</sup> formula ''f'' is satisfied by some CSP process ''P'' if all executions of ''P'' satisfy ''f''. If there is an execution of ''P'' which violates the property f, then the test <tt>P |= f</tt> fails by providing a counterexample. Depending on whether f expresses a safety or liveness property a finite path or a path in lasso-form (, i.e. a path leading to a cycle) is returned as a counterexample, respectively. | An LTL<sup>[e]</sup> formula ''f'' is satisfied by some CSP process ''P'' if all executions of ''P'' satisfy ''f''. If there is an execution of ''P'' which violates the property ''f'', then the test <tt>P |= f</tt> fails by providing a counterexample. Depending on whether ''f'' expresses, a safety or liveness property, a finite path or a path in lasso-form (, i.e. a path leading to a cycle) is returned as a counterexample, respectively. | ||
Note that ProB supports also Past-LTL<sup>[e]</sup>. Past-LTL<sup>[e]</sup>, however, | Note that ProB supports also Past-LTL<sup>[e]</sup>. Past-LTL<sup>[e]</sup>, however, may be considered to be inappropriate for LTL assertions since the goal of this type of assertions is usually to check whether all executions starting at the initial states of the process satisfy the respective LTL<sup>[e]</sup>. | ||
To check whether a process ''P'' satisfies a CTL formula f the following assertion should be made: | To check whether a process ''P'' satisfies a CTL formula ''f'' the following assertion should be made: | ||
<tt>assert P |= CTL: “f”</tt> | <tt>assert P |= CTL: “f”</tt> | ||
As for LTL, CTL formulae should be put in between quotes. The CTL syntax for CSP-M specifications could be | As for LTL, CTL formulae should be put in between quotes. The CTL syntax for CSP-M specifications could be summarised as follows: | ||
* Atomic propositions: | * Atomic propositions: | ||
** To check if an event `evt` is enabled in a state use `e(evt)` | ** To check if an event `evt` is enabled in a state use `e(evt)` | ||
| Line 86: | Line 86: | ||
* Next executed event: | * Next executed event: | ||
** `EX [e] true`: | ** `EX [e] true`: | ||
Note that these two types of assertions, the LTL and CTL assertions, are not part of the CSP-M language supported by FDR2. Loading a CSP-M file in FDR2 having assertion declarations of this form will exit with a syntax error. Bear in mind to remove or comment out such LTL/CTL assertions in the CSP-M file before loading it in FDR2. | Note that these two types of assertions, the LTL and CTL assertions, are not part of the CSP-M language supported by FDR2. Loading a CSP-M file in FDR2 having assertion declarations of this form will exit with a syntax error. Bear in mind to remove or comment out such LTL/CTL assertions in the CSP-M file before loading it in FDR2. | ||
Revision as of 09:16, 2 September 2015
As of version 1.3.4, ProB provides support for refinement checking and various other assertions (deadlock, divergence, determinism, and LTL/CTL assertions) of CSP-M specifications. In this tutorial we give a short overview of the ProB’s implementations and features for checking CSP assertions. In the Tcl/Tk interface of ProB, CSP assertions can be assembled and checked in the CSP Assertions Viewer. A description of the CSP Assertions Viewer is also given.
Supported CSP Assertions in ProB
ProB provides support for checking almost all types of CSP-M assertions that can be checked within FDR2. Besides the assertion types that can be checked in FDR2, in ProB one also can check temporal properties on processes expressed by means of LTL and CTL formulae.[1] The following types of assertions are supported in ProB:
Refinement
Refinement is one of the fundamental notions for construction and verification of systems specified in CSP. Given two CSP processes P and Q one can state in ProB the property that process Q is an ‘m’ refinement of P by the following assertion declaration:
assert P [m= Q
where m indicates one of the following types of comparison: ‘T’ for traces, ‘F’ for failures, ‘FD’ for failures-divergence, ‘R’ for refusals, and ‘RD’ for ‘refusals-divergence’. Note that the refinement types ‘V’ (revivals) and ‘VD’ (revivals-divergence) that are part of the refinement assertions supported by FDR2 are yet not supported by ProB.
Deadlock
Stating assertions about CSP processes to be deadlock-free is possible by the following assertion declaration:
assert P :[deadlock free [m]]
where P is a process expression and m indicates one of the following models: ‘F’ (failures) and ‘FD’ (failures-divergence).
Determinism
Stating assertions about CSP processes to be deterministic is possible by the following assertion declaration:
assert P :[deterministic [m]]
where P is a process expression and m one of the following models: ‘F’ (failures) and ‘FD’ (failures-divergence).
Livelock
Stating assertions about CSP processes to be livelock-free is possible by the following assertion declaration:
assert P :[livelock free]
where P is a process expression.
Temporal Properties
In ProB it is also possible to make assertions about temporal properties of CSP processes both in LTL and CTL. Basically, one wants to check whether some process P satisfies a formula f expressed in temporal logic (denoted by P |= f).
To check whether a process P satisfies an LTL formula f write the following declaration:
assert P |= LTL: “f”
Note that f must be placed between quotes and that the satisfaction relation |= is immediately followed by `LTL:`. ProB supports LTL[e], an extended version of LTL which provides additionally support for making propositions on transitions. The following LTL[e] syntax for CSP-M specifications can be outlined by the following rules:
- Atomic propositions:
- To check if an event `evt` is enabled in a state use `e(evt)`
- Transition propositions:
- To check whether an event `evt` is executed use `[evt]`
- Logical operators
- true and false
- `not`: negation
- `&`,`or`,and `=>`: conjunction, disjunction and implication
- Temporal operators:
- `G f`: globally
- `F f`: finally
- `X f`: next
- `f U g`: until
- `f W g`: weak-until
- `f R g`: release
- Fairness operators:
- `WF(evt)` or `wf(evt)`: weak fairness, where `evt` is an event
- `SF(evt)` or `sf(evt)`: strong fairness, where `evt` is an event
- `WEF` and `SEF` for checking LTL[e] formulae on executions that are strongly and weakly fair with respect to all events, respectively
An LTL[e] formula f is satisfied by some CSP process P if all executions of P satisfy f. If there is an execution of P which violates the property f, then the test P |= f fails by providing a counterexample. Depending on whether f expresses, a safety or liveness property, a finite path or a path in lasso-form (, i.e. a path leading to a cycle) is returned as a counterexample, respectively.
Note that ProB supports also Past-LTL[e]. Past-LTL[e], however, may be considered to be inappropriate for LTL assertions since the goal of this type of assertions is usually to check whether all executions starting at the initial states of the process satisfy the respective LTL[e].
To check whether a process P satisfies a CTL formula f the following assertion should be made:
assert P |= CTL: “f”
As for LTL, CTL formulae should be put in between quotes. The CTL syntax for CSP-M specifications could be summarised as follows:
- Atomic propositions:
- To check if an event `evt` is enabled in a state use `e(evt)`
- Transition propositions:
- To check whether an event `evt` is executed use `[evt]`
- State formulae, where f, f1 and f2 are path formulae:
- true | false | `not` f | f1 `&` f2 | f1 `or` f2 | f1 `=>` f2,
- E f : path quantifier \exists, pronounced `for some path`
- A f : path quantifier \forall, pronounced `for all paths`
- Path formulae, where g, g1 and g2 are state formulae:
- `X g`: next
- `g1 U g2`: until
- `G g`: globally
- `F g`: finally
- Next executed event:
- `EX [e] true`:
Note that these two types of assertions, the LTL and CTL assertions, are not part of the CSP-M language supported by FDR2. Loading a CSP-M file in FDR2 having assertion declarations of this form will exit with a syntax error. Bear in mind to remove or comment out such LTL/CTL assertions in the CSP-M file before loading it in FDR2.
CSP Assertions Viewer
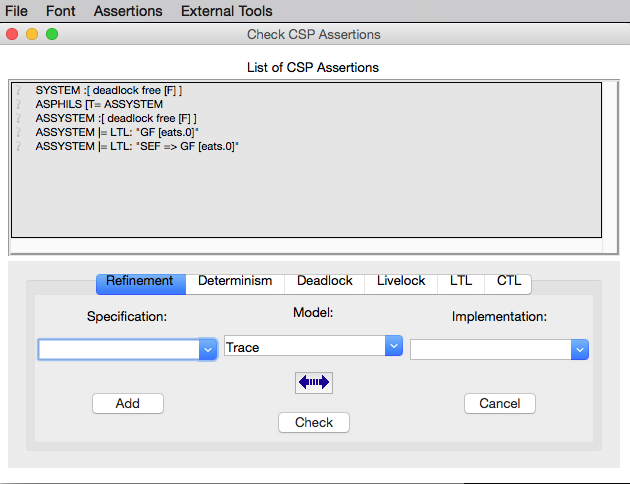
When a CSP-M specification is loaded one can open the CSP Assertion Viewer either from the menu bar of the main window by selecting the `Check CSP-M Assertions` command in the `Verify` menu or from the Refinement button in the ‘’State Properties’’ pane. The viewer looks as follows:
The CSP Assertion Viewer of ProB has a similar design to the graphical user interface of FDR2. It consists basically of three main components: menu bar, list box and a tab pane. In the following each of the components and its corresponding functionalities are thoroughly described.
The Menu Bar
The menu bar is placed at the top of the window. On OS X, it is placed at the top of the screen. The menu bar includes several menus providing commands for adjusting, executing and changing the items in the list box, as well as some (standard) options for re-loading the model, saving the items to an external file or the loaded file, and launching some external tools related with the domain in which the list items are checked. Each menu can be popped up by a click with Mouse-1 (usually the left mouse button). The menu bar consists of the following menus and menu commands:
- File
- Reopen File: Reopening (re-reading and re-loading) the currently loaded file, incorporating any changes that may have been made since the file was last loaded.
- Copy new Assertions to File: All assertions that have been added to the list box since the currently loaded file was last read will be written to the file, i.e. all assertions that are yet not in the file are appended to it.
- Save Assertions to External File: Selecting the option opens a standard Tk dialog box requesting a name of a file in which the assertions and their results in the list box could be saved.
- Exit: Closing the CSP Assertion Viewer. Any assertion check results and any recently added assertions from the Tab Pane will get lost. The user will not be prompted to save these to the source file or an external file.
- Font
Changing the font settings of the elements in the list box. Each of the items of this menu is a cascading menu that provides a number of options to be selected. The currently selected option in the cascading menu is marked by a tick symbol (✓).- Family-Name: Change the font family of the text in the list box. There are currently four font families that could be chosen: Arial, Curier, Helvetica, and Times. Default font is Curier.
- Size: Change the font size of the text in the list box. Default font size is 10.
- Background: Change the background color of the list box. Default background color is Gray90.
- Assertions
- Uncheck All Assertions: Set the status of all assertions in the list box to non-checked.
- Delete All Assertions: Delete all assertions in the list box.
- Check All Refinement…: The item is a cascading menu and provides commands to check all assertions of one of the following supported refinement types: Traces, Failures, Failures-Divergence, Refusals, and Refusals-Divergence.
- Check Processes for…: The item is a cascading menu and provides commands to check all assertions of the following supported types of checks: Deadlock, Determinism and Livelock.
- Check All LTL Assertions: Selecting this command causes ProB to check all LTL assertions in the list box that are not checked yet.
- Check All CTL Assertions: Selecting this command causes ProB to check all CTL assertions in the list box that are not checked yet.
- Check All Assertions: Selecting this command causes ProB to check of all assertions in the list box that are not checked yet.
- External Tools
- Open Specification with FDR: Open the currently loaded CSP-M specification in FDR2. The FDR2 tool is launched with the currently loaded specification in case the FDR2 is installed and the correct path to the `fdr2` command is set for the respective preference `Path to the FDR2 tool`. The value of the `Path to the FDR2 tool` preference can be changed from the “CSP Preferences…” window which can be opened by selecting the `CSP Preferences…` command in `Preferences` menu.
- Evaluate with CSPM-Interpreter: Selecting this command opens a console in which one can evaluate CSP-M expressions using the CSP-M interpreter. The CSP-M interpreter is an external tool implemented independently from ProB. CSP-M expression can be evaluated if the `cspm` tool is installed and the path to the cspm-command is set for the respective preference `Path to CSPM tool`. The command is obsolete and its removal is considered in future.
The Assertion List Box
This part of the viewer lists all assertions stated in the currently loaded CSP-M specification and provides a set of features for checking, manipulating, and debugging of CSP assertions in the list. To each statement in the assertion list box a symbol is assigned, placed on the left side of it, that reveals the current status of the statement in the viewer:
- ? - Assertion not checked yet.
- ✔ - Assertion check completed successfully.
- ✘ - Assertion check completed, but a counterexample was found to the stated property. The debugger can be used to explore the reason why the property does not hold.
- ⌚ - Assertion is currently checked.
- ! – The check of the assertion not completed for some reason. Possible causes for the interruption may be:
- Syntax error in the property was detected;
- Assertion check failed because of missing implementation;
- Assertion check interrupted by user.
Note that in case of an LTL and a CTL assertion the check could fail to complete because of a syntax error in the respective formula. If an assertion check fails to complete an error box is popped up displaying an error message, which indicates why the assertion check could not be completed.
An assertion can be selected by clicking on it with Mouse-1 and checked by double-clicking on it with Mouse-1. Alternatively, selecting an assertion and then pressing the Enter key can start the respective assertion check. When an assertion check is in progress, the assertion will be marked by the clock symbol. If the assertion check is completed without interrupting it, a new status is assigned to the assertion: tick symbol indicating that the assertion was completed successfully or cross symbol indicating that a counterexample was found to the stated property. In case that the status is cross the counterexample can be explored by (second) double-click with Mouse-1 on the assertion or by selecting the assertion and then pressing the Enter key. If the respective assertion is negated, i.e. there is `not` in front of the assertion property, and marked with a cross, then no counterexample can be explored as the proper statement holds.
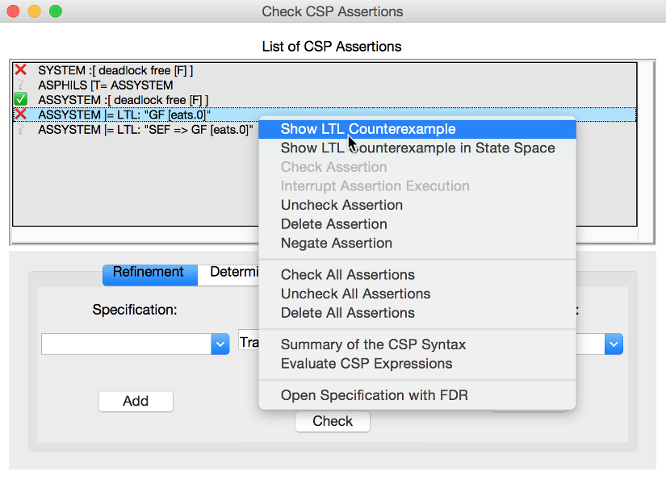
The list box is equipped with a contextual menu (or a pop-up menu), which appears when you right-click on an assertion in the list. Depending on the type and the status of the assertion the contextual menu provides options for checking, debugging, modifying the respective assertion, as well as various other options. Take, for example, the selected assertion on which the contextual menu is popped up in the picture below.
The assertion "ASSYSTEM |= LTL: “GF [eats.0]”" intends to check if the process ASSYSTEM satisfies the LTL formula "GF [eats.0]". For the selected assertion above, for example, the options `Show LTL Counterexample` and `Show LTL Counterexample in State Space` are enabled as a counterexample was found for the check. On the other hand, the options `Check Assertion` and `Interrupt Assertion` are disabled as the assertion check was completed.
The contextual menu has in general the following options:
The following options affect only the assertion being selected.
- Debug or Show LTL/CTL Counterexample…: Opens the graphical viewer for exploring the counterexample that was found for the respective LTL assertion check. Option is enabled if the assertion is not negated and its status is cross, or if the assertion is negated and its status is tick. Option appears if the assertion type is an LTL assertion or a CTL assertion.
- Debug Assertion: Opens a trace-failure debugger window showing the reason why the corresponding assertion check failed. Option is enabled if the assertion is not negated and its status is cross, or if the assertion is negated and its status is tick. Option available for all types of assertions except for LTL and CTL assertions.
- Check Assertion: Starts immediately the check of the assertion being selected before right clicking on it.
- Interrupt Assertion Check: Interrupts the current assertion check.
- Uncheck Assertion: If the assertion was checked and the result of the check is different from question mark, then the status of the assertion will be reset to question mark. Option is enabled only if the assertion result is different from question mark.
- Delete Assertion: Removes the selected item from the assertion list.
- Negate Assertion: Negates the respective assertion. In case the result of the (proper) assertion check is cross, then the result of the negated assertion becomes tick. Otherwise, if the result of the (proper) assertion is tick, the negated assertion becomes cross.
- Swap Processes: Option available only for refinement assertions. Performing the command causes the attachment of a new refinement assertion in which the process expressions on both sides of the refinement operator `[m=` are swapped. If, for example, we execute ‘’Swap Processes’’ on the assertion "P [T= Q", the command adds to the list of assertions the assertion "Q [T= P".
The following options affect all assertions in the list box.
- Check All Assertions: The command causes the check of all assertions in the list box. The assertions that are already checked would not be checked again.
- Uncheck All Assertions: The status of all assertions in the list box is reset to question mark.
- Delete All Assertions: All entries in the list box are removed. As a result the message “No assertions were added.” appears in the list box.
Other options. The following options have no impact on the assertions in the list box.
- Summary of the CSP Syntax: Opens a window in which the summary of the CSP-M syntax and features supported by the ProB tool is detailed.
- Evaluate CSP Expressions: Opens the Eval console in which CSP expressions can be evaluated.
- Open Specification with FDR: Opens the currently loaded CSP-M specification in FDR2. The FDR2 tool is launched with the currently loaded specification if the FDR2 is installed and the correct path to the `fdr2` command is set for the respective preference `Path to the FDR2 tool`. The value of the `Path to the FDR2 tool` preference can be changed from the “CSP Preferences…” window which can be opened by selecting the `CSP Preferences…` command in `Preferences` menu.
The Tab Pane
The tab pane is placed at the bottom of the window and enables the user to construct and check properties of processes of the currently loaded CSP-M file without adding explicitly assertions to the file.
There are overall six tab pages. Each tab page is used to build up new assertion statements. The tab pages provide selectors, entries and command buttons for assembling, adding and checking new assertions. In each of the selectors all possible processes of the loaded CSP-M file are accessible. It is also possible to specify new process expressions by entering these in the respective entry of the process selector. The tab pages for creating LTL and CTL assertions provide additionally an appropriate entry for specifying the according LTL and CTL formula intended to be checked on the specified process, respectively.
Each tab page is equipped with the following command buttons:
- Add: Attaching a new assertion to the list of assertions in the list box. If the entry in one of the selectors is empty no assertion will be added to list box and a warning message will appear informing the user that some of the entries were not specified. If the entered assertion in the tab page is already in the list box, then a warning box appears informing the user that the assertion is already in the list box. If the assertion is present in the list box it will not be added.
- Check: Attaching a new assertion to the list of assertions in the list box and immediately starting checking the assertion. If the assertion is already in the list box, then the user will be informed that the assertion is already in the list box and in case it is not checked yet its check will be started.
- Cancel/Interrupt: Closes the window or interrupts an assertion check. In case the “Cancel” command is executed all checks and new assertions will get lost. If an assertion is currently checked, then the button command “Cancel” is replaced by another button command ‘’Interrupt’’, which causes the interruption of the current assertion check when the button is clicked.
Debugging Non-satisfied Assertions
In case an assertion check has failed the user can explore the reason for the assertion violation. If the corresponding assertion is not negated and after finishing the assertion check is marked by cross, then this is an indication that ProB has found a counterexample for the check. The counterexample can be explored by a second double-click with the ‘Mouse-1’ button or by selecting the assertion and then pressing the ‘Enter’ button. Depending on the type of the assertion and the type of the counterexample a corresponding debugging window is opened.
If a CSP process violates an LTL formula or a universally quantified CTL formula, then by performing a second double-click on the respective assertion one can explore the provided counterexample by means of the graphical viewer (Graphical Viewer).
In the following we give an overview of the features for debugging counterexamples being found for different refinement checks. Consider the following CSP processes:
P = a -> b -> c -> STOP
Q = a -> (b -> Q [] c -> Q)
R = a -> b -> R
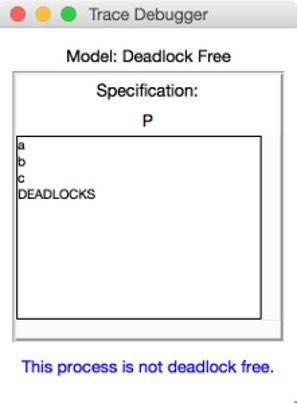
If we intend to check whether P is deadlock free, then we can state the assertion
assert P :[deadlock free [F]].
The check of the assertion will finish by marking the assertion in the list box with a cross symbol. The cross symbol indicates that a counterexample was found for the assertion checks. The counterexample is basically given by the trace <a,b,c> as obviously `P` reaches a deadlock state after performing the trace <a,b,c>. Providing a second double-click on the assertion will open the following debugging window:
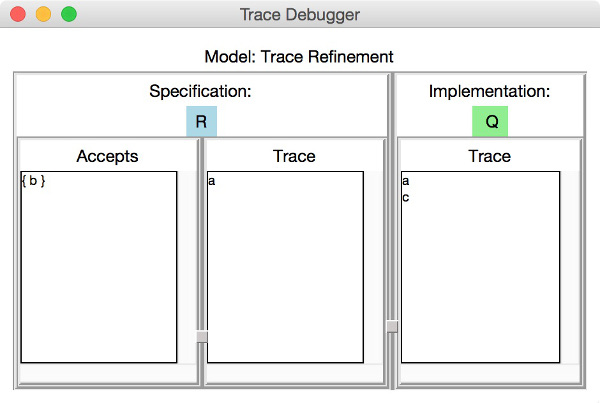
Considering the CSP process `Q` and `R` one can see or check that `R` is a trace refinement of `Q` as `R` performs the same set of traces as `Q`. Thus, the assertion check for `Q [T= R` will mark the assertion statement in the list box by a tick symbol. On the other hand, checking the assertion `R [T= Q` will find a counterexample for the refinement check. Performing a second double-click on the item `R [T= Q` will open the following trace debugger window with the counterexample displayed in it:
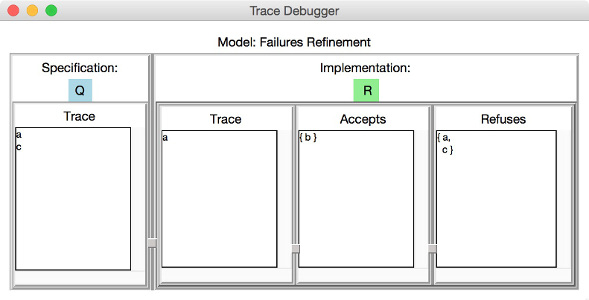
A counterexample of a trace-refinement assertion is a trace leading to a state in which the implementation process performs an event that the specification process cannot perform. In the example above both processes `P` and `Q` perform the trace <a> and reach states in which the implementation process can perform an event that is not offered by the specification process. One can easily deduce from the picture above that `Q` performs after `a` the event `c` which is not offered by `R` as `R` can perform only `b` after `a`. In the left most column `Accept` the debugger window lists all possible events that are offered by the specification process after performing the trace given in the `Trace` column next to `Accepts`.
As we already mentioned above `R` is a trace-refinement of `Q`. On the other hand, checking whether `R` is a failures-refinement of `Q` will produce a counterexample as `R` refuses the event `c` that is offered by Q after executing `a`. Accordingly, the counterexample will be illustrated within the following trace debugger window:
These are basically the three types of debugging windows that will appear when debugging a counterexample for an assertion check in case the respective assertion is not an LTL or a CTL assertion. When a counterexample for an LTL assertion is found it will be explored in the graphical viewer, the same graphical viewer that is used for visualizing the state space of the loaded models in ProB.
Let us observe again the CSP process `Q` and suppose we want to check whether `Q` satisfies the LTL formula `F [c]`. Then, the respective LTL assertion is declared as follows:
assert Q |= LTL: “F [c]”
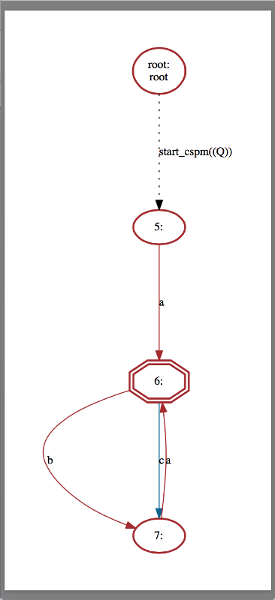
The assertion check will produce a counterexample as `Q` obviously reaches a cycle “(b -> a)+” that violates the property “F [c]”. Performing a second double-click on the assertion will display the following state space graph in the graphical viewer:
In the figure above, the nodes and the transitions of the respective counterexample "a -> (b -> a)+" are coloured in red.
Checking CSP Assertions with `probcli`
It is also possible to check CSP assertions with the command line version of ProB. The command has the following syntax:
probcli -csp_assertion "A" File
where A is a CSP assertion and File the path to the CSP file. For example, if we want to check the refinement assertion `P [T= Q` on some CSP specification `example.csp`, then we can do this by running the ProB command line version with the following options:
probcli -csp_assertion "P [T= Q" example.csp
Note that the assertion should be placed between quotes. In addition, when an assertion is checked with the '-csp_assertion' option the keyword assert should be omitted.
References and Notes
- ↑ ProB provides support for LTL and CTL model checking (citations needed).