Tutorial Various Optimizations: Difference between revisions
m moved Tutorial Model Checking with Various Optimizations to Tutorial Various Optimizations: Link to homepage to long. |
|||
| Line 23: | Line 23: | ||
</pre> | </pre> | ||
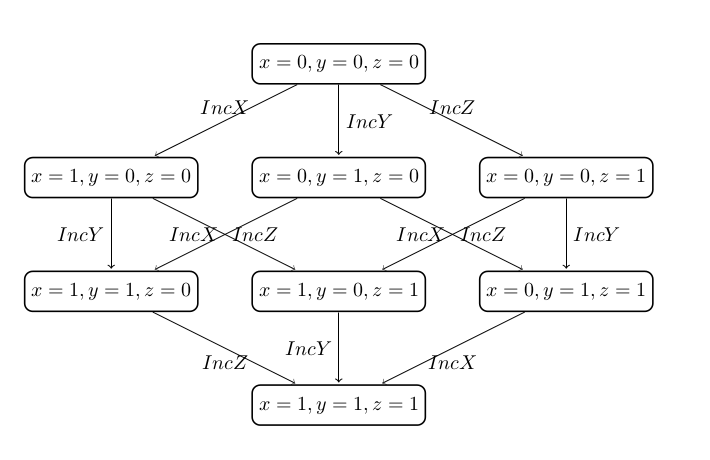
The machine has a deadlock state. The deadlock state will be reached by executing each of the operations IncX, IncY, and IncZ. The order of executing the operations is irrelevant with respect to reaching the deadlock state. This can be seen, for example, by observing the full state space of the machine | The machine has a deadlock state. The deadlock state will be reached by executing each of the operations IncX, IncY, and IncZ. The order of executing the operations is irrelevant with respect to reaching the deadlock state. This can be seen, for example, by observing the full state space of the machine: | ||
[[File:full_state_space_por.png]] | [[File:full_state_space_por.png]] | ||
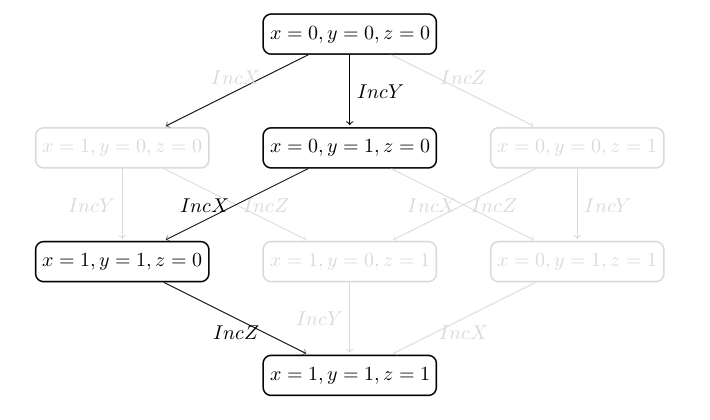
Since the order in which the operations are executed is not relevant for discovering the deadlock state it is sufficient to examine only one of the six paths that start in the initial state and reach the deadlock. Thus, for the | Since the order in which the operations are executed is not relevant for discovering the deadlock state it is sufficient to examine only one of the six paths that start in the initial state and reach the deadlock. Thus, for the machine it is enough to analyze only one arbitrary order of the events in order to detect the deadlock: | ||
[[File:partial_state_space_por.png]] | [[File:partial_state_space_por.png]] | ||
Using this observation the ordinary model checker of ProB has been extended to check a model formalized in B or Event-B using partial order reduction. More information about the implementation of POR in ProB and the theoretical background of POR can be read here | Using this observation the ordinary model checker of ProB has been extended to check a model formalized in B or Event-B using partial order reduction. More information about the implementation of POR in ProB and the theoretical background of POR can be read [http://www.stups.uni-duesseldorf.de/mediawiki/images/5/5b/Pub-DobrikovLeuschelPORtechreport.pdf here]. Our implementation of POR uses the ample set theory <ref>E.M. Clarke, O. Grumberg, M. Minea, and D. Peled: ''State Space Reduction using Partial Order Reduction''. STTT '98, 3, pages 279-287</ref>. | ||
For enabling the POR optimization for the model checker in Tcl/Tk interface of ProB a new check box “Partial Order Reduction” has been added to the “Model Checker” menu. Note that the option shows up only when the user mode is set to “Normal” (see Preferences → User Mode in the menu bar). The POR optimization can be enabled for model checking B and Event-B models with the command line version of ProB by setting the 'por' preference to the value 'ample_sets'. For example, the machine ''Example'' can be checked for deadlock and invariant violations using the POR optimization with the command line version of ProB as follows: | For enabling the POR optimization for the model checker in Tcl/Tk interface of ProB a new check box “Partial Order Reduction” has been added to the “Model Checker” menu. Note that the option shows up only when the user mode is set to “Normal” (see Preferences → User Mode in the menu bar). The POR optimization can be enabled for model checking B and Event-B models with the command line version of ProB by setting the 'por' preference to the value 'ample_sets'. For example, the machine ''Example'' can be checked for deadlock and invariant violations using the POR optimization with the command line version of ProB as follows: | ||
Revision as of 16:12, 17 March 2015
| Warning This page has not yet been reviewed. Parts of it may no longer be up to date |
The ordinary model checker of ProB enables the user to verify automatically whether a B model contains any errors such as deadlocks and invariant violations. The search for errors is performed by a graph traversal algorithm exploring the state space until an error state has been found or all states of the model have been explored. The runtime of the model checker is mostly determined by the number of states of the model being analyzed and thus model checking is generally limited by the size of the state space of the model. The problem is also known as the state space explosion problem.
To combat the state space explosion problem two advantageous techniques, partial guard evaluation and partial order reduction, for the ordinary model checker of ProB have been implemented for model checking practically B and Event-B models with huge state spaces. This tutorial describes how one can apply model checking using the optimizations and additionally gives hints when it is recommendable to use these optimizations.
Partial Order Reduction
Partial order reduction (POR) is a method proposed for combating the state space explosion problem by means of state space reduction. The technique takes advantage of the commutativity of concurrently executed actions. The reduction relies on selecting a subset of all enabled actions in each reachable state of the state space aiming in this way to reduce the number of possible orderings of actions. Basically, the idea is to check only a fragment of the original state space that is sufficient for checking the given property.
Take, for example, the following B machine:
MACHINE Example VARIABLES x,y,z INVARIANT x:INT & y:INT & z:INT INITIALISATION x,y,z:=0,0,0 OPERATIONS IncX = PRE x=0 THEN x:= x+1 END; IncY = PRE y=0 THEN y:= y+1 END; IncZ = PRE z=0 THEN z:= z+1 END END
The machine has a deadlock state. The deadlock state will be reached by executing each of the operations IncX, IncY, and IncZ. The order of executing the operations is irrelevant with respect to reaching the deadlock state. This can be seen, for example, by observing the full state space of the machine:
Since the order in which the operations are executed is not relevant for discovering the deadlock state it is sufficient to examine only one of the six paths that start in the initial state and reach the deadlock. Thus, for the machine it is enough to analyze only one arbitrary order of the events in order to detect the deadlock:
Using this observation the ordinary model checker of ProB has been extended to check a model formalized in B or Event-B using partial order reduction. More information about the implementation of POR in ProB and the theoretical background of POR can be read here. Our implementation of POR uses the ample set theory [1].
For enabling the POR optimization for the model checker in Tcl/Tk interface of ProB a new check box “Partial Order Reduction” has been added to the “Model Checker” menu. Note that the option shows up only when the user mode is set to “Normal” (see Preferences → User Mode in the menu bar). The POR optimization can be enabled for model checking B and Event-B models with the command line version of ProB by setting the 'por' preference to the value 'ample_sets'. For example, the machine Example can be checked for deadlock and invariant violations using the POR optimization with the command line version of ProB as follows:
********* DETERMINE ACTION DEPENDENCIES AND ENABLE GRAPH ************* ********** FINISHED ANALYSIS ************* Analysis Checking Time: 10 ms. ALL OPERATIONS COVERED found_error(deadlock,3) finding_trace_from_to(root) Model Checking Time: 40 ms (100 ms walltime) States analysed: 3 Transitions fired: 4 *** COUNTER EXAMPLE FOUND *** deadlock *** TRACE: 1: INITIALISATION(0,0,0): 2: IncZ: 3: IncX: 4: IncY: ! *** error occurred *** ! deadlock
As a result the deadlock has been discovered by exploring in total 3 states using the Mixed DF/BF search strategy. Model checking the machine without using POR will possibly explore more states until it finds out the deadlock state (recall that the full state space of Example.mch consists of 8 states). Note that the POR algorithm can be applied to all exploration strategies (DF, BF, and Mixed DF/BF) of the ordinary model checker of ProB.
The reduction of the state space takes effect by choosing a subset of the set of all enabled transitions in the currently explored state. The set of all enabled transitions in some state s is usually denoted by enabled(s) and the subset of the transitions chosen to be executed in s is denoted by ample(s). The set ample(s) we call an ample set for state s. Each ample set should satisfy certain conditions (the ample set requirements) in order to guarantee that the reduction of the state space is sound in regard to the property being checked on the model. In fact, there are four conditions that each ample set should satisfy:
- (A 1) ample(s) = {} <=> enabled(s) = {}
- (A 2) Along every finite execution in the original state space starting in s, an event dependent on ample(s) cannot appear before some event e:ample(s) is executed
- (A 3) If ample(s) is a proper set of enabled(s), then each transition in ample(s) is a stutter transition.
- (A 4) For any cycle C in the reduced state space, if a state in C has an enabled event e, then there exists a state s in C such that e:ample(s).
To guarantee that all deadlocks in the full state space are also preserved in the reduced state space it is sufficient when all computed ample sets satisfy just the first two conditions <citation needed>. This suggests that in some cases, when we check for deadlock freedom only, the reduction of the state space may be more effective if each ample set satisfies only the first two ample set requirements. That is, model checking with POR usually tends to yield more state space reduction when checking a model for deadlock freedom only than checking it for invariant violations or simultaneously for deadlock freedom and invariant violations. (The reduction algorithm of ProB has been adapted to this fact.) For this reason, keep in mind to disable the “Invariant Violations” option if it is intended to check a B or Event-B model just for deadlocks using the POR optimization as the potential for more significant reduction of the state space is higher.
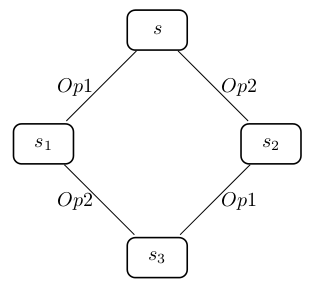
The reduction algorithm makes use of the independence of transitions. Two transitions Op1 and Op2 are called independent if for each state s where both are enabled we have the following situation:
Let us assume that the transitions Op1 and Op2 in Figure <refer> constitute the executions of two deterministic operations of a B machine. Then we can say that the operations Op1 and Op2 are independent, when they cannot disable one other and additionally both possible orders of execution of the operations <Op1,Op2> and <Op2,Op1> starting in some state s reach the same state s3. If two transitions are not independent, then both are denoted as dependent.
To find out whether two operations are independent one can analyze the syntactical structure of both operations. If each of the operations modifies variables of the machine not read by the other one and if both operations modify different variables, then these operations are considered to be independent. Besides performing only a syntactical analysis, we use also the constraint-based facilities of ProB to determine more exact relations between the operations. The reason for those extra analyzes lies in the high potential for significant reduction of the state space when the degree of independence of the checked B model is high.
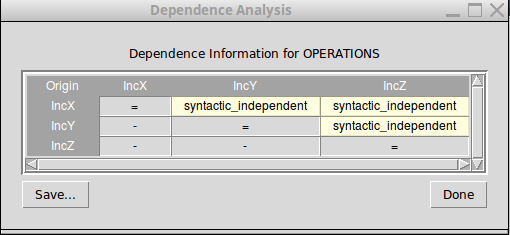
Thus, if we have a great amount of independent operations for some B machine, then we have a great potential for significant state space reduction. The results of the analyses for determining the independence of operations for a particular B machine, which are used by the reduction algorithm for computing the ample sets, can be viewed in the menu bar of the Tcl/Tk interface of ProB: “Verify → Enabling Analysis → Dependence Analysis (Table)”. For example, the dependency table for the model 'Example.mch' looks as follows:
The results in the dependency table for a pair of operations Op1 and Op2 have the following meanings:
- 'syntactic_independent': op1 and op2 are syntactically independent; both events write different variables and no one of the events can write a variable which is read by the other one
- 'independent': one of the events or both events write variables read only in the guard of the other one, though the events cannot disable each other
- 'dependent': the events are not independent
- 'race_dependent': Op1 and Op2 have write variables in common
- '-': the dependency relation is symmetric, see (Op2,Op1) result
- '=': Op1 and Op2 represent the same event
To sum up, in order to take an advantage of POR the model being checked should have many independent operations. Thus, it is advisable to use the reduced search when the analyzed model has comparatively many independent operations. For example, if a B model has no pair of independent operations or all independent operations are not executed concurrently, i.e. two independent operations are never simultaneously enabled, then no reductions of the state space will be performed using the reduced search algorithm.
Partial Guard Evaluation
(tbd)
- ↑ E.M. Clarke, O. Grumberg, M. Minea, and D. Peled: State Space Reduction using Partial Order Reduction. STTT '98, 3, pages 279-287