Game of Life: Difference between revisions
Created page with 'This is a simple model of Conway's Game of Life. It was written for animation with ProB. One interesting aspect is that the simulation is unbounded, i.e., not restricted to some …' |
No edit summary |
||
| Line 62: | Line 62: | ||
END | END | ||
</pre> | </pre> | ||
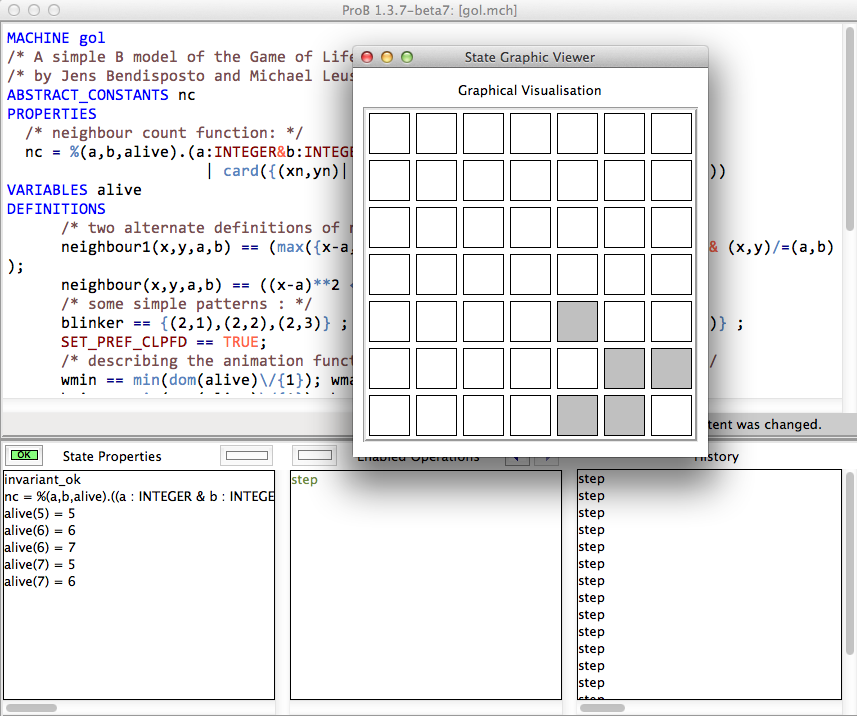
The following is a screenshot of ProB Tcl/Tk animating the above model: | |||
[[File:ProB_GameOfLife_Screenshot.png|600px|center]] | |||
Revision as of 07:20, 5 September 2013
This is a simple model of Conway's Game of Life. It was written for animation with ProB. One interesting aspect is that the simulation is unbounded, i.e., not restricted to some pre-determined area of the grid.
MACHINE gol
/* A simple B model of the Game of Life */
/* by Jens Bendisposto and Michael Leuschel */
ABSTRACT_CONSTANTS nc
PROPERTIES
/* neighbour count function: */
nc = %(a,b,alive).(a:INTEGER&b:INTEGER & alive <: INTEGER*INTEGER
| card({(xn,yn)| (xn,yn) : alive & neighbour(xn,yn,a,b)}))
VARIABLES alive
DEFINITIONS
neighbour(x,y,a,b) == (max({x-a,a-x}) : {0,1} & max({y-b,b-y}) : {0,1} & (x,y)/=(a,b));
INVARIANT
alive <: INTEGER * INTEGER & alive /= {}
INITIALISATION
alive := {(2,1),(2,2),(2,3)} /* blinker */
OPERATIONS
step = alive := {(u1,v1) | (u1,v1):alive & nc(u1,v1,alive) : {2,3} } \/
{(u2,v2) | #(a2,b2).((a2,b2):alive & neighbour(u2,v2,a2,b2)) & /* restrict enumeration to neighbours of alive */
(u2,v2)/:alive & nc(u2,v2,alive)=3 }
END
If you want to visualize the simulation using ProB's Tk graphical viewer one needs to add a definition for the animation function. This leads to the following B model (where we have also added an alternate definition of the neighbourhood relationship):
MACHINE gol
/* A simple B model of the Game of Life */
/* by Jens Bendisposto and Michael Leuschel */
ABSTRACT_CONSTANTS nc
PROPERTIES
/* neighbour count function: */
nc = %(a,b,alive).(a:INTEGER&b:INTEGER & alive <: INTEGER*INTEGER
| card({(xn,yn)| (xn,yn) : alive & neighbour(xn,yn,a,b)}))
VARIABLES alive
DEFINITIONS
/* two alternate definitions of neighbour relationship; both work */
neighbour1(x,y,a,b) == (max({x-a,a-x}) : {0,1} & max({y-b,b-y}) : {0,1} & (x,y)/=(a,b));
neighbour(x,y,a,b) == ((x-a)**2 <= 1 & (y-b)**2 <=1 & (x,y)/=(a,b));
/* some simple patterns : */
blinker == {(2,1),(2,2),(2,3)} ; glider == {(1,2),(2,3),(3,1),(3,2),(3,3)} ;
SET_PREF_CLPFD == TRUE;
/* describing the animation function for the graphical visualization : */
wmin == min(dom(alive)\/{1}); wmax == max(dom(alive)\/{1});
hmin == min(ran(alive)\/{1}); hmax == max(ran(alive)\/{1});
ANIMATION_FUNCTION_DEFAULT == ( (wmin..wmax)*(hmin..hmax)*{0} );
ANIMATION_FUNCTION == ( alive * {1} );
ANIMATION_IMG0 == "images/sm_empty_box.gif";
ANIMATION_IMG1 == "images/sm_gray_box.gif"
INVARIANT
alive <: INTEGER * INTEGER & alive /= {}
INITIALISATION
alive := glider
OPERATIONS
step = alive := {(u1,v1) | (u1,v1):alive & nc(u1,v1,alive) : {2,3} } \/
{(u2,v2) | #(a2,b2).((a2,b2):alive & neighbour(u2,v2,a2,b2)) & /* restrict enumeration to neighbours of alive */
(u2,v2)/:alive & nc(u2,v2,alive)=3 }
END
The following is a screenshot of ProB Tcl/Tk animating the above model: