Alloy: Difference between revisions
No edit summary |
|||
| Line 224: | Line 224: | ||
P iff Q equivalence | P iff Q equivalence | ||
not P negation | not P negation | ||
Alternative syntax: | Alternative syntax: | ||
| Line 234: | Line 231: | ||
P <=> Q equivalence | P <=> Q equivalence | ||
! P negation | ! P negation | ||
Quantifiers: | |||
------------- | |||
all DECL | P universal quantification | |||
some DECL | P existential quantification | |||
one DECL | P existential quantification with exactly one solution | |||
lone DECL | P quantification with one or zero solutions | |||
where the DECL follow the following form: | |||
x : S choose a singleton subset of S (like x : one S) | |||
x : one S choose a singleton subset of S | |||
x : S choose x to be any subset of S | |||
x : some S choose x to be any non-empty subset of S | |||
x : lone S choose x to be empty or a singleton subset of S | |||
x : Rel where Rel is a cartesian product / relation: see multiplicity declarations x in Rel | |||
x,y... : S, v,w,... : T means x:S and y : S and ... v:T and w:T and ... | |||
disjoint x,y,... : S means x : S and y : S and ... and x,y,... are all pairwise distinct | |||
Set Expressions: | Set Expressions: | ||
---------------- | ---------------- | ||
univ all objects | univ all objects | ||
none empty set | none empty set | ||
S + T set union | S + T set union | ||
S & T set intersection | S & T set intersection | ||
S - T set difference | S - T set difference | ||
# S | # S cardinality of set | ||
Set Predicates: | Set Predicates: | ||
--------------- | --------------- | ||
no S set S is empty | no S set S is empty | ||
S in T R is subset of S | S in T R is subset of S | ||
S = T set equality | S = T set equality | ||
some S set S is not empty | S != T set inequality | ||
one S S is singleton set | some S set S is not empty | ||
lone S S is empty or a singleton | one S S is singleton set | ||
lone S S is empty or a singleton | |||
{x:S | P} set comprehension | |||
{DECL | P} set comprehension, DECL has same format as for quantifiers | |||
let s : S | P identifier definition | |||
Relation Expressions: | Relation Expressions: | ||
---------------------- | ---------------------- | ||
R -> S Cartesian product | R -> S Cartesian product | ||
R . S relational join | R . S relational join | ||
S <: R domain restriction of relation R for unary set S | S <: R domain restriction of relation R for unary set S | ||
R :> S range restriction of relation R for unary set S | R :> S range restriction of relation R for unary set S | ||
~R relational inverse | R ++ Q override of relation R by relation Q | ||
^R transitive closure of binary relation | ~R relational inverse | ||
*R reflexive and transitive closure | ^R transitive closure of binary relation | ||
*R reflexive and transitive closure | |||
Multiplicity Declarations: | |||
--------------------------- | |||
The following multiplicity annotations are supported for binary (sub)-relations: | |||
f in S -> T f is any relation from S to T (subset of cartesian product) | |||
f in S -> lone T f is a partial function from S to T | |||
f in S -> one T f is a total function from S to T | |||
f in S -> some T f is a total relation from S to T | |||
f in S one -> one T f is a total bijection from S to T | |||
f in S lone -> lone T f is a partial injection from S to T | |||
f in S lone -> one T f is a total injection from S to T | |||
f in S some -> lone T f is a partial surjection from S to T | |||
f in S some -> one T f is a total surjection from S to T | |||
f in S some -> T f is a surjective relation from S to T | |||
f in S some -> some T f is a total surjective relation from S to T | |||
Ordered Signatures: | |||
------------------- | |||
A signature S can be defined to be ordered: | |||
open util/ordering [S] as s | |||
s/first first element | |||
s/last last element | |||
s/next[s2] element after s2 | |||
s/nexts[s2] all elements after s2 | |||
s/prev[s2] element before s2 | |||
s/prevs[s2] all elements before s2 | |||
Sequences: | |||
---------- | |||
s : seq S ordered and indexed sequence | |||
s.first head element | |||
s.rest tail of the sequence | |||
s.idxOf [x] returns the first index of the occurence of x in s, returns the empty set if x does not occur in s | |||
s.insert[i,x] returns a new sequence where x is inserted at index position i | |||
Arithmetic Expressions and Predicates: | Arithmetic Expressions and Predicates: | ||
| Line 267: | Line 323: | ||
You need to open util/integer: | You need to open util/integer: | ||
plus[X,Y] addition | plus[X,Y] addition | ||
minus[X,Y] subtraction | minus[X,Y] subtraction | ||
mul[X,Y] multiplication | mul[X,Y] multiplication | ||
div[X,Y] division | div[X,Y] division | ||
rem[X,Y] remainder | rem[X,Y] remainder | ||
sum[S] sum of integers of set S | sum[S] sum of integers of set S | ||
X < Y less | |||
X = Y integer equality | |||
X != Y integer inequality | |||
X > Y greater | |||
X =< Y less or equal | |||
X >= Y greater or equal | |||
Structuring: | |||
------------ | |||
fact NAME { PRED } | |||
fact NAME (x1,...,xk : Set) { PRED } | |||
pred NAME { PRED } | |||
pred NAME (x1,...,xk : Set) { PRED } | |||
assert NAME { PRED } | |||
fun NAME : Type { EXPR } | |||
Commands: | |||
--------- | |||
run NAME | |||
check NAME | |||
run NAME for x global scope of less or equal x | |||
run NAME for exactly x1 but x2 S global scope of x1 but less or equal x2 S | |||
run NAME for x1 S1,...,xk Sk individual scopes for signatures S1,..,Sk | |||
run NAME for x Int specify the integer bitwidth (integer overflows might occur) | |||
</pre> | </pre> | ||
Revision as of 07:53, 2 October 2018
As of version 1.8 ProB provides support to load Alloy models.
The Alloy models are translated to B machines by a Java frontend.
This work and web page is still experimental.
The work is based on a translation of the specification language Alloy to classical B. The translation allows us to load Alloy models into ProB in order to find solutions to the model's constraints. The translation is syntax-directed and closely follows the Alloy grammar. Each Alloy construct is translated into a semantically equivalent component of the B language. In addition to basic Alloy constructs, our approach supports integers and orderings.
Installation
Alloy2B is included with the lastest nightly builds of ProB.
You can build it yourself:
- Clone or download Alloy2B project on Github.
- Make jar file (gradle build) and
- put resulting alloy2b-*.jar file into ProB's lib folder.
Examples
N-Queens
module queens
open util/integer
sig queen { x:Int, x':Int, y:Int } {
x >= 1
y >= 1
x <= #queen
y <= #queen
x' >=1
x' <= #queen
x' = minus[plus[#queen,1],x]
}
fact { all q:queen, q':(queen-q) {
! q.x = q'.x
! q.y = q'.y
! plus[q.x,q.y] = plus[q'.x,q'.y]
! plus[q.x',q.y] = plus[q'.x',q'.y]
}}
pred show {}
run show for exactly 4 queen, 5 int
This can be loaded in ProB, as shown in the following screenshot. To run the "show" command you have to use "Find Sequence..." command for "run_show" in the "Constraint-Based Checking" submenu of the "Verify" menu.
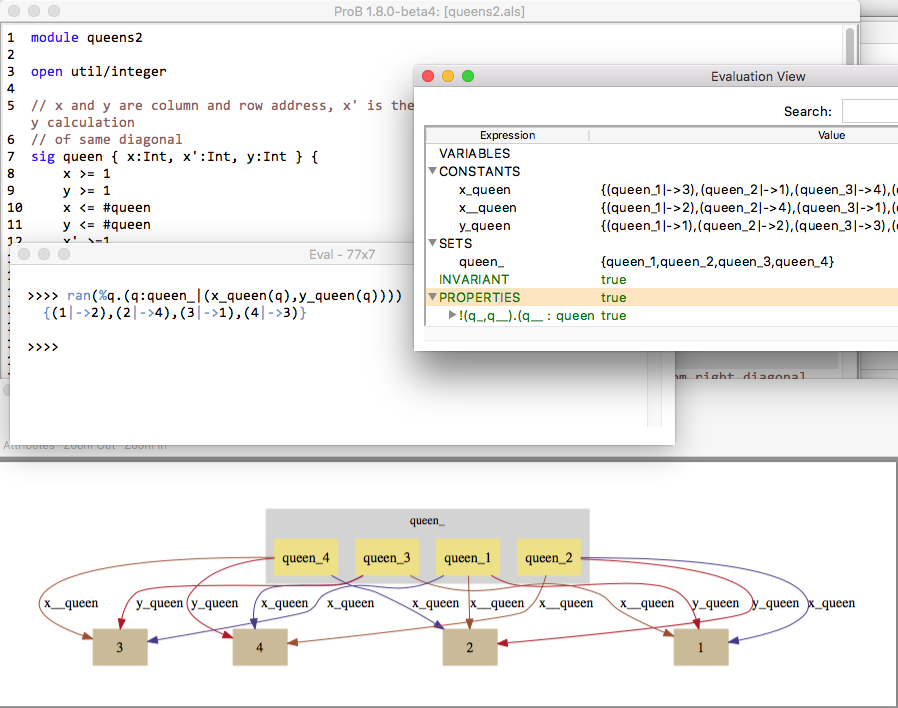
Internally the Alloy model is translated to the following B model:
/*@ generated */
MACHINE queens
SETS queen_
CONSTANTS x_queen, x__queen, y_queen
DEFINITIONS
show_ == 1=1 ;
SET_PREF_MAXINT == 15 ; SET_PREF_MININT == -16
PROPERTIES
(!(q_, q__).({q_} <: queen_ & {q__} <: (queen_ - {q_}) =>
(not((x_queen(q_) = x_queen(q__)))) & (not((y_queen(q_) = y_queen(q__))))
& (not(((x_queen(q_) + y_queen(q_)) = (x_queen(q__) + y_queen(q__)))))
& (not(((x__queen(q_) + y_queen(q_)) = (x__queen(q__) + y_queen(q__))))))) &
card(queen_) = 4 &
/* from signature declaration */ !(this_).({this_} <: queen_ =>
((x_queen(this_) >= 1)) & ((y_queen(this_) >= 1))
& ((x_queen(this_) <= card(queen_)))
& ((y_queen(this_) <= card(queen_)))
& ((x__queen(this_) >= 1)) & ((x__queen(this_) <= card(queen_)))
& ((x__queen(this_) = ((card(queen_) + 1) - x_queen(this_))))) &
x_queen : queen_ --> INT &
x__queen : queen_ --> INT &
y_queen : queen_ --> INT
OPERATIONS
run_show = PRE show_ THEN skip END
END
River Crossing Puzzle
module river_crossing
open util/ordering[State]
abstract sig Object { eats: set Object }
one sig Farmer, Fox, Chicken, Grain extends Object {}
fact { eats = Fox->Chicken + Chicken->Grain}
sig State { near, far: set Object }
fact { first.near = Object && no first.far }
pred crossRiver [from, from', to, to': set Object] {
one x: from | {
from' = from - x - Farmer - from'.eats
to' = to + x + Farmer
}
}
fact {
all s: State, s': s.next {
Farmer in s.near =>
crossRiver [s.near, s'.near, s.far, s'.far]
else
crossRiver [s.far, s'.far, s.near, s'.near]
}
}
run { last.far=Object } for exactly 8 State
This can be loaded in ProB, as shown in the following screenshot. To run the "show" command you have to use "Find Sequence..." command for "run_show" in the "Constraint-Based Checking" submenu of the "Verify" menu (after enabling Kodkod in the Preferences menu).
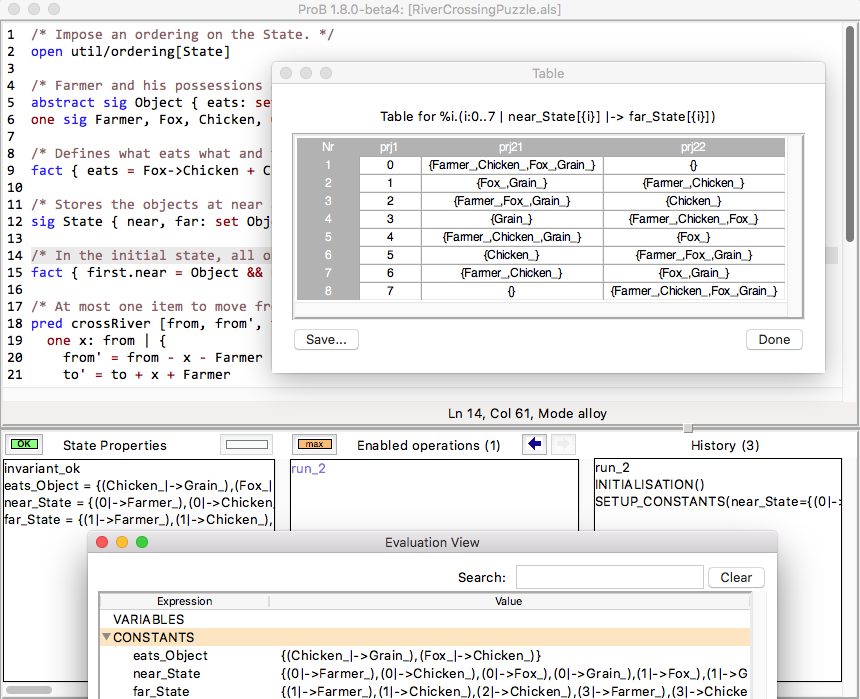
Internally the Alloy model is translated to the following B model:
/*@ generated */
MACHINE river_crossing
SETS
Object_
CONSTANTS
Farmer_, Fox_, Chicken_, Grain_, eats_Object, near_State, far_State
DEFINITIONS
crossRiver_(from_,from__,to_,to__) == from_ <: Object_
& from__ <: Object_ & to_ <: Object_
& to__ <: Object_ & (card({x_ | {x_} <: from_
& (((from__ = (((from_ - {x_}) - {Farmer_}) - eats_Object[from__])))
& ((to__ = ((to_ \/ {x_}) \/ {Farmer_}))))}) = 1) ;
next_State_(s) == {x|x=s+1 & x:State_} ;
nexts_State_(s) == {x|x>s & x:State_} ;
prev_State_(s) == {x|x=s-1 & x:State_} ;
prevs_State_(s) == {x|x<s & x:State_} ;
State_ == 0..7
PROPERTIES
{Farmer_} <: Object_ &
{Fox_} <: Object_ &
{Chicken_} <: Object_ &
{Grain_} <: Object_ &
((eats_Object = (({Fox_} * {Chicken_}) \/ ({Chicken_} * {Grain_})))) &
(((near_State[{min(State_)}] = Object_) & far_State[{min(State_)}] = {})) &
(!(s_, s__).({s_} <: State_ & {s__} <: next_State_(s_) =>
((({Farmer_} <: near_State[{s_}]) =>
crossRiver_(near_State[{s_}], near_State[{s__}],
far_State[{s_}], far_State[{s__}]))
& (not(({Farmer_} <: near_State[{s_}])) =>
crossRiver_(far_State[{s_}], far_State[{s__}],
near_State[{s_}], near_State[{s__}]))))) &
Farmer_ /= Fox_ &
Farmer_ /= Chicken_ &
Farmer_ /= Grain_ &
Fox_ /= Chicken_ &
Fox_ /= Grain_ &
Chicken_ /= Grain_ &
{Farmer_} \/ {Fox_} \/ {Chicken_} \/ {Grain_} = Object_ &
eats_Object : Object_ <-> Object_ &
near_State : State_ <-> Object_ &
far_State : State_ <-> Object_
OPERATIONS
run_2 = PRE (far_State[{max(State_)}] = Object_) THEN skip END
END
Proof with Atelier-B Example
sig Object {}
sig Vars {
src,dst : Object
}
pred move (v, v': Vars, n: Object) {
v.src+v.dst = Object
n in v.src
v'.src = v.src - n
v'.dst = v.dst + n
}
assert add_preserves_inv {
all v, v': Vars, n: Object |
move [v,v',n] implies v'.src+v'.dst = Object
}
check add_preserves_inv for 3
Note that our translation does not (yet) generate an idiomatic B encoding, with move as B operation
and src+dst=Object as invariant: it generates a check operation encoding the predicate add_preserves_inv with universal quantification.
Below we shoe the B machine we have input into AtelierB. It was obtained by pretty-printing from \prob, and putting the negated guard
of theadd_preserves_inv into an assertion (so that AtelierB generates the desired proof obligation).
MACHINE alloytranslation
SETS /* deferred */
Object_; Vars_
CONCRETE_CONSTANTS
src_Vars, dst_Vars
PROPERTIES
src_Vars : Vars_ --> Object_
& dst_Vars : Vars_ --> Object_
ASSERTIONS
!(v_,v__,n_).(v_ : Vars_ & v__ : Vars_ & n_ : Object_
=>
(src_Vars[{v_}] \/ dst_Vars[{v_}] = Object_ &
v_ |-> n_ : src_Vars &
src_Vars[{v__}] = src_Vars[{v_}] - {n_} &
dst_Vars[{v__}] = dst_Vars[{v_}] \/ {n_}
=>
src_Vars[{v__}] \/ dst_Vars[{v__}] = Object_)
)
END
The following shows AtelierB proving the above assertion:
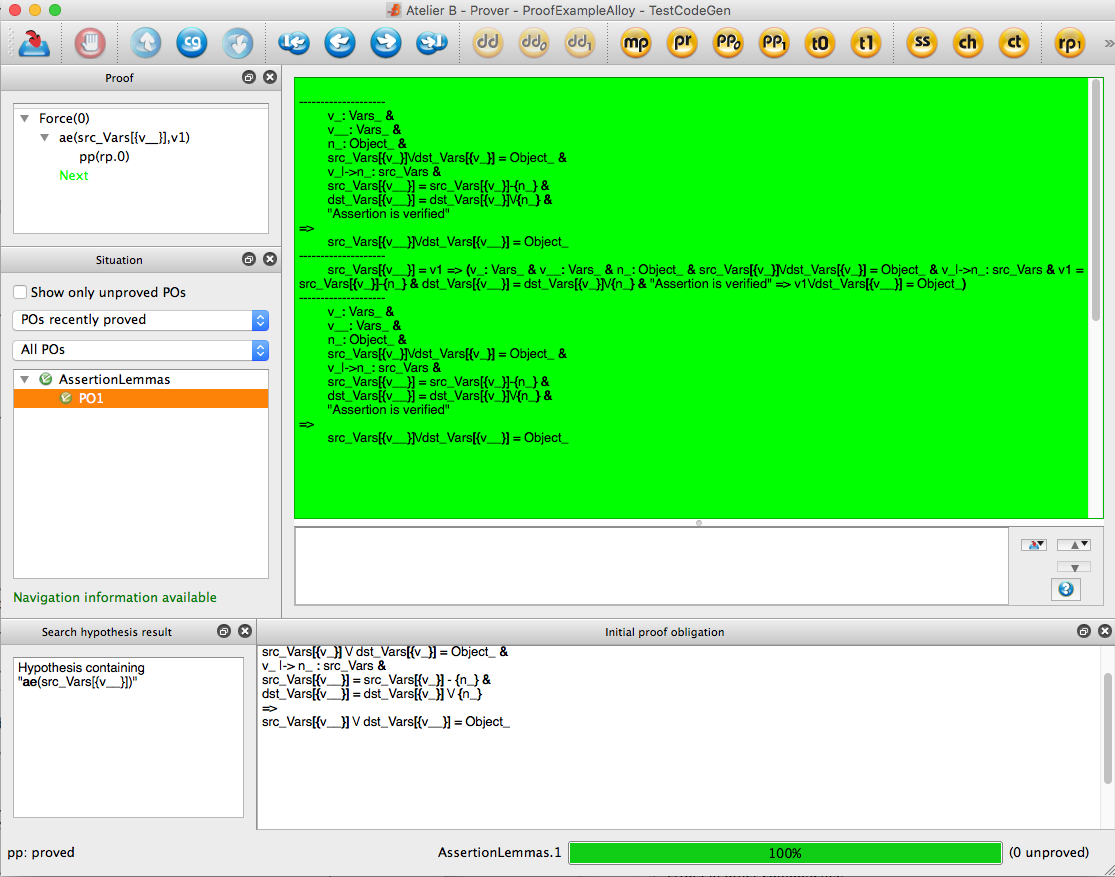
Alloy Syntax
Logical predicates:
-------------------
P and Q conjunction
P or Q disjunction
P implies Q implication
P iff Q equivalence
not P negation
Alternative syntax:
P && Q conjunction
P || Q disjunction
P => Q implication
P <=> Q equivalence
! P negation
Quantifiers:
-------------
all DECL | P universal quantification
some DECL | P existential quantification
one DECL | P existential quantification with exactly one solution
lone DECL | P quantification with one or zero solutions
where the DECL follow the following form:
x : S choose a singleton subset of S (like x : one S)
x : one S choose a singleton subset of S
x : S choose x to be any subset of S
x : some S choose x to be any non-empty subset of S
x : lone S choose x to be empty or a singleton subset of S
x : Rel where Rel is a cartesian product / relation: see multiplicity declarations x in Rel
x,y... : S, v,w,... : T means x:S and y : S and ... v:T and w:T and ...
disjoint x,y,... : S means x : S and y : S and ... and x,y,... are all pairwise distinct
Set Expressions:
----------------
univ all objects
none empty set
S + T set union
S & T set intersection
S - T set difference
# S cardinality of set
Set Predicates:
---------------
no S set S is empty
S in T R is subset of S
S = T set equality
S != T set inequality
some S set S is not empty
one S S is singleton set
lone S S is empty or a singleton
{x:S | P} set comprehension
{DECL | P} set comprehension, DECL has same format as for quantifiers
let s : S | P identifier definition
Relation Expressions:
----------------------
R -> S Cartesian product
R . S relational join
S <: R domain restriction of relation R for unary set S
R :> S range restriction of relation R for unary set S
R ++ Q override of relation R by relation Q
~R relational inverse
^R transitive closure of binary relation
*R reflexive and transitive closure
Multiplicity Declarations:
---------------------------
The following multiplicity annotations are supported for binary (sub)-relations:
f in S -> T f is any relation from S to T (subset of cartesian product)
f in S -> lone T f is a partial function from S to T
f in S -> one T f is a total function from S to T
f in S -> some T f is a total relation from S to T
f in S one -> one T f is a total bijection from S to T
f in S lone -> lone T f is a partial injection from S to T
f in S lone -> one T f is a total injection from S to T
f in S some -> lone T f is a partial surjection from S to T
f in S some -> one T f is a total surjection from S to T
f in S some -> T f is a surjective relation from S to T
f in S some -> some T f is a total surjective relation from S to T
Ordered Signatures:
-------------------
A signature S can be defined to be ordered:
open util/ordering [S] as s
s/first first element
s/last last element
s/next[s2] element after s2
s/nexts[s2] all elements after s2
s/prev[s2] element before s2
s/prevs[s2] all elements before s2
Sequences:
----------
s : seq S ordered and indexed sequence
s.first head element
s.rest tail of the sequence
s.idxOf [x] returns the first index of the occurence of x in s, returns the empty set if x does not occur in s
s.insert[i,x] returns a new sequence where x is inserted at index position i
Arithmetic Expressions and Predicates:
--------------------------------------
You need to open util/integer:
plus[X,Y] addition
minus[X,Y] subtraction
mul[X,Y] multiplication
div[X,Y] division
rem[X,Y] remainder
sum[S] sum of integers of set S
X < Y less
X = Y integer equality
X != Y integer inequality
X > Y greater
X =< Y less or equal
X >= Y greater or equal
Structuring:
------------
fact NAME { PRED }
fact NAME (x1,...,xk : Set) { PRED }
pred NAME { PRED }
pred NAME (x1,...,xk : Set) { PRED }
assert NAME { PRED }
fun NAME : Type { EXPR }
Commands:
---------
run NAME
check NAME
run NAME for x global scope of less or equal x
run NAME for exactly x1 but x2 S global scope of x1 but less or equal x2 S
run NAME for x1 S1,...,xk Sk individual scopes for signatures S1,..,Sk
run NAME for x Int specify the integer bitwidth (integer overflows might occur)