Rush Hour Puzzle: Difference between revisions
Created page with 'This case studies tackles encoding the [http://en.wikipedia.org/wiki/Rush_Hour_(board_game) rush hour board game] in which cars are packed on a 6-by-6 grid and can either move ho…' |
No edit summary |
||
| Line 119: | Line 119: | ||
The encoding of puzzle 40 in the file RushHour/Puzzle40.def is as follows: | The encoding of [http://www.puzzles.com/products/RushHour/RHfromMarkRiedel/Jam.html?40 hardest puzzle Nr 40] in the file RushHour/Puzzle40.def is as follows: | ||
<pre> | <pre> | ||
DEFINITIONS | DEFINITIONS | ||
| Line 133: | Line 133: | ||
INIT_HCAR == {1|->2, 2|->4, 3|->1, 4|->5, 5|->1, 6|->4} | INIT_HCAR == {1|->2, 2|->4, 3|->1, 4|->5, 5|->1, 6|->4} | ||
</pre> | </pre> | ||
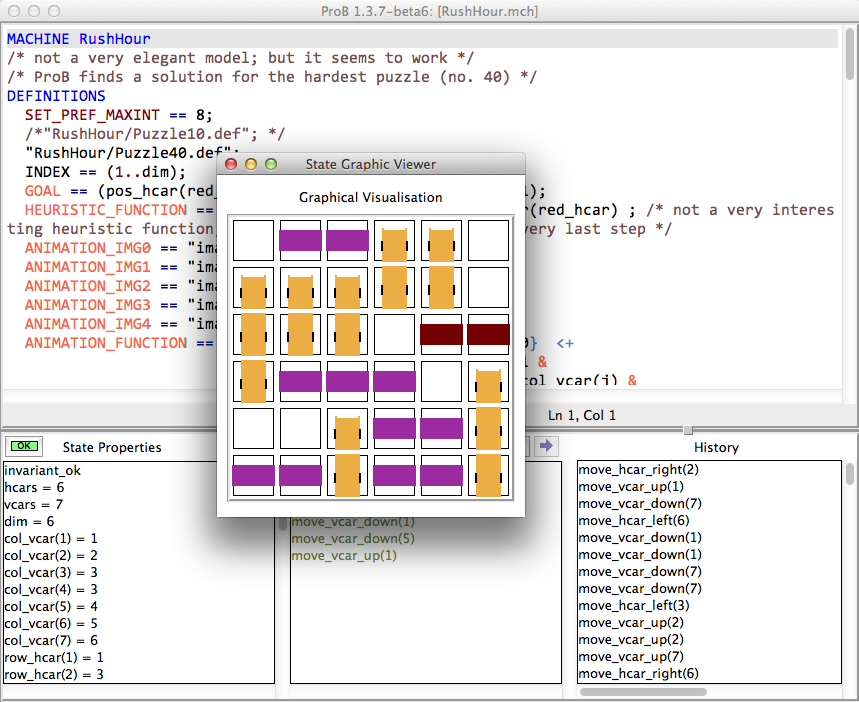
ProB 1.3.7 took about 26 seconds to solve this puzzle (on my Mac Book Air 1.8 GHz i7); | |||
[[File:ProB_RushHour_Screenshot.png|600px|center]] | |||
Revision as of 11:45, 30 July 2013
This case studies tackles encoding the rush hour board game in which cars are packed on a 6-by-6 grid and can either move horizontally or vertically. The goal is to move the red car to the exit. In this particular instance we try to solve the hardest puzzle Nr 40.
MACHINE RushHour
/* not a very elegant model; but it seems to work */
/* ProB finds a solution for the hardest puzzle (no. 40) */
DEFINITIONS
SET_PREF_MAXINT == 8;
/*"RushHour/Puzzle10.def"; */
"RushHour/Puzzle40.def";
INDEX == (1..dim);
GOAL == (pos_hcar(red_hcar) >= dim-size_hcar(red_hcar)+1);
HEURISTIC_FUNCTION == dim-size_hcar(red_hcar) - pos_hcar(red_hcar) ; /* not a very interesting heuristic function; as red_car can only be moved at very last step */
ANIMATION_IMG0 == "images/sm_empty_box.gif";
ANIMATION_IMG1 == "images/sm_vcar.gif";
ANIMATION_IMG2 == "images/sm_vcar_front.gif";
ANIMATION_IMG3 == "images/sm_hcar.gif";
ANIMATION_IMG4 == "images/sm_red_hcar.gif";
ANIMATION_FUNCTION == ( {r,c,i|r:1..dim & c:1..dim & i=0} <+
{r,c,i|r:1..dim & c:1..dim & i=1 &
#j.(j:dom(col_vcar) & c=col_vcar(j) &
r>pos_vcar(j) & r<pos_vcar(j)+size_vcar(j)) } <+
{r,c,i|r:1..dim & c:1..dim & i=2 &
#j.(j:dom(col_vcar) & c=col_vcar(j) & r=pos_vcar(j)) } <+
{r,c,i|r:1..dim & c:1..dim & i:3..4 &
#j.(j:dom(row_hcar) & r=row_hcar(j) &
c>=pos_hcar(j) & c<pos_hcar(j)+size_hcar(j) &
((j=red_hcar & i=4) or (j/=red_hcar & i=3)) ) }
);
POSs_VCAR(vc) == {c,r|c=col_vcar(vc) & r>=pos_vcar(vc) & r<pos_vcar(vc)+size_vcar(vc)};
POSs_HCAR(hc) == {c,r|r=row_hcar(hc) & c>=pos_hcar(hc) & c<pos_hcar(hc)+size_hcar(hc)}
CONSTANTS
vcars,hcars,dim, col_vcar, row_hcar, size_vcar, size_hcar,
red_hcar
PROPERTIES
/* The particular puzzle */
STATIC_PROPS
&
dim = 6 &
vcars : NATURAL1 & hcars: NATURAL1 &
col_vcar: 1..vcars --> INDEX &
row_hcar: 1..hcars --> INDEX &
size_vcar: 1..vcars --> INDEX &
size_hcar: 1..hcars --> INDEX &
red_hcar : 1..hcars &
/* vcars are in ascending in row order */
!r.(r:1..(vcars-1) => col_vcar(r)<=col_vcar(r+1)) &
/* hcars are in ascending in col order */
!c.(c:1..(hcars-1) => row_hcar(c)<=row_hcar(c+1))
VARIABLES
pos_vcar,
pos_hcar
INVARIANT
pos_vcar: 1..vcars --> INDEX &
pos_hcar: 1..hcars --> INDEX
ASSERTIONS
!(vc,hc).(vc:1..vcars & hc:1..hcars => POSs_VCAR(vc) /\ POSs_HCAR(hc) = {});
!(vc1,vc2).(vc1:1..(vcars-1) & vc2:2..vcars & vc1<vc2 => POSs_VCAR(vc1) /\ POSs_VCAR(vc2) = {});
!(hc1,hc2).(hc1:1..(hcars-1) & hc2:2..hcars & hc1<hc2 => POSs_HCAR(hc1) /\ POSs_HCAR(hc2) = {})
INITIALISATION
pos_vcar := INIT_VCAR ||
pos_hcar := INIT_HCAR
OPERATIONS
move_hcar_right(car) =
PRE car:1..hcars &
pos_hcar(car)<=dim - size_hcar(car) & /* car not at extreme right */
(car<hcars => (row_hcar(car) /= row_hcar(car+1) or
pos_hcar(car+1) > pos_hcar(car)+size_hcar(car))) &
!cv.(cv:1..vcars & col_vcar(cv)=pos_hcar(car)+size_hcar(car) =>
row_hcar(car) /: pos_vcar(cv)..pos_vcar(cv)+size_vcar(cv)-1)
THEN
pos_hcar(car) := pos_hcar(car)+1
END;
move_hcar_left(car) =
PRE car:1..hcars &
pos_hcar(car)> 1 & /* car not at extreme left */
(car>1 => (row_hcar(car) /= row_hcar(car-1) or
pos_hcar(car-1)+size_hcar(car-1) <= pos_hcar(car)-1))&
!cv.(cv:1..vcars & col_vcar(cv)=pos_hcar(car)-1 =>
row_hcar(car) /: pos_vcar(cv)..pos_vcar(cv)+size_vcar(cv)-1)
THEN
pos_hcar(car) := pos_hcar(car)-1
END;
move_vcar_down(car) =
PRE car:1..vcars &
pos_vcar(car)<=dim - size_vcar(car) & /* car not at extreme bottom */
(car<vcars => (col_vcar(car) /= col_vcar(car+1) or
pos_vcar(car+1) > pos_vcar(car)+size_vcar(car))) &
!cv.(cv:1..hcars & row_hcar(cv)=pos_vcar(car)+size_vcar(car) =>
col_vcar(car) /: pos_hcar(cv)..pos_hcar(cv)+size_hcar(cv)-1)
THEN
pos_vcar(car) := pos_vcar(car)+1
END;
move_vcar_up(car) =
PRE car:1..vcars &
pos_vcar(car)> 1 & /* car not at extreme top */
(car>1 => (col_vcar(car) /= col_vcar(car-1) or
pos_vcar(car-1)+size_vcar(car-1) <= pos_vcar(car)-1)) &
!cv.(cv:1..hcars & row_hcar(cv)=pos_vcar(car)-1 =>
col_vcar(car) /: pos_hcar(cv)..pos_hcar(cv)+size_hcar(cv)-1)
THEN
pos_vcar(car) := pos_vcar(car)-1
END
END
The encoding of hardest puzzle Nr 40 in the file RushHour/Puzzle40.def is as follows:
DEFINITIONS
/* The particular puzzle (nr. 40) */
STATIC_PROPS ==
(vcars=7 & hcars = 6 &
col_vcar = {1|->1, 2|->2, 3|->3, 4|->3, 5|->4, 6|->5, 7|->6} &
size_vcar = {1|->3, 2|->2, 3|->2, 4|->2, 5|->2, 6|->2, 7|->3} &
row_hcar = {1|->1, 2|->3, 3|->4, 4|->5, 5|->6, 6|->6} &
size_hcar = {1|->2, 2|->2, 3|->3, 4|->2, 5|->2, 6|->2} &
red_hcar = 2); /* red hcar */
INIT_VCAR == {1|->1, 2|->2, 3|->2, 4|->5, 5|->4, 6|->1, 7|->2 };
INIT_HCAR == {1|->2, 2|->4, 3|->1, 4|->5, 5|->1, 6|->4}
ProB 1.3.7 took about 26 seconds to solve this puzzle (on my Mac Book Air 1.8 GHz i7);