Tutorial Rodin Parameters: Difference between revisions
| (6 intermediate revisions by 2 users not shown) | |||
| Line 22: | Line 22: | ||
In Rodin, there are only the mathematical integers, and there is no MININT or MAXINT constant. | In Rodin, there are only the mathematical integers, and there is no MININT or MAXINT constant. | ||
However, this preference will be used by ProB if it cannot determine the value of an integer | However, this preference will be used by ProB if it cannot determine the value of an integer | ||
variable | variable in order to know in which range it should be enumerated. | ||
== Size of unspecified sets == | == Size of unspecified sets (carrier sets) == | ||
This is the third entry in the | This is the third entry in the screen shot above. | ||
ProB requires all carrier sets to be finite and ProB has to know the cardinality before starting the animation or model checking. | ProB requires all carrier sets to be finite and ProB has to know the cardinality before starting the animation or model checking. | ||
| Line 35: | Line 35: | ||
such as <tt>card(S)=4</tt>, then this value will be used. | such as <tt>card(S)=4</tt>, then this value will be used. | ||
You can also use <tt>card(S)<n</tt> to specify a maximum cardinality, or <tt>card(S)>n</tt> to specify a minimum cardinality. | You can also use <tt>card(S)<n</tt> to specify a maximum cardinality, or <tt>card(S)>n</tt> to specify a minimum cardinality. | ||
If no cardinality is specified, ProB will use the default size provided in the preferences dialog (the entry "Size of unspecified deferred sets..."). | |||
Note that you can create a new context with those axioms just for animation or model checking with ProB. | === Using contexts for ProB animation === | ||
Note that you can create a new context with those axioms just for animation or model checking with ProB. For this you can simply right-click on the context and use the Rodin command "EXTEND". | |||
For example, in Camille syntax such a context could look like: | |||
context c1_prob extends c1 | |||
axioms | |||
@prob_axm card(S) = 3 | |||
end | |||
After that you can also refine the model you want to animate by right-clicking on it and using the Rodin command "REFINE", and then add the new context to the seen context list: | |||
machine m0_prob refines m0 sees c0 c1_prob | |||
If ProB cannot infer the size of a carrier set | Here the machine m0_prob and c1_prob play the role of configuration files for the animation. | ||
You can also add additional axioms in c1_prob to force ProB to use a specific valuation of your constants. | |||
If ProB cannot infer the size of a carrier set; it will use the default value provided in the "Size of unspecified sets" preference. | |||
Note that for complicated machines it can be tricky to set up the cardinalities of the carrier sets correctly. | |||
For example, if you have an axiom <tt>f : A -->> B</tt>, then the cardinality of <tt>A</tt> must be greater or equal to the cardinality of <tt>B</tt>. We are working on an automated analysis for detecting the correct cardinalities of the carrier sets automatically. | |||
==== Transforming deferred carrier sets into enumerated sets ==== | |||
Instead of providing a cardinality you can also transform a deferred set into | |||
an enumerated set, i.e., provided an enumeration of all its elements. | |||
Here is how you would instantiate S to be a set containing the three elements named a,b,c: | |||
context c1_prob extends c1 | |||
constants a,b,c | |||
axioms | |||
@prob_axm partition(S,{a},{b},{c}) | |||
end | |||
Latest revision as of 12:31, 24 September 2019
Preferences
You can modify the most important parameters of ProB by going to the Rodin preferences.
Now selecting the ProB pane inside the Rodin preferences. You see that a relatively large list of preferences appears (the actual number and denotation depends on the exact version of ProB you have installed):
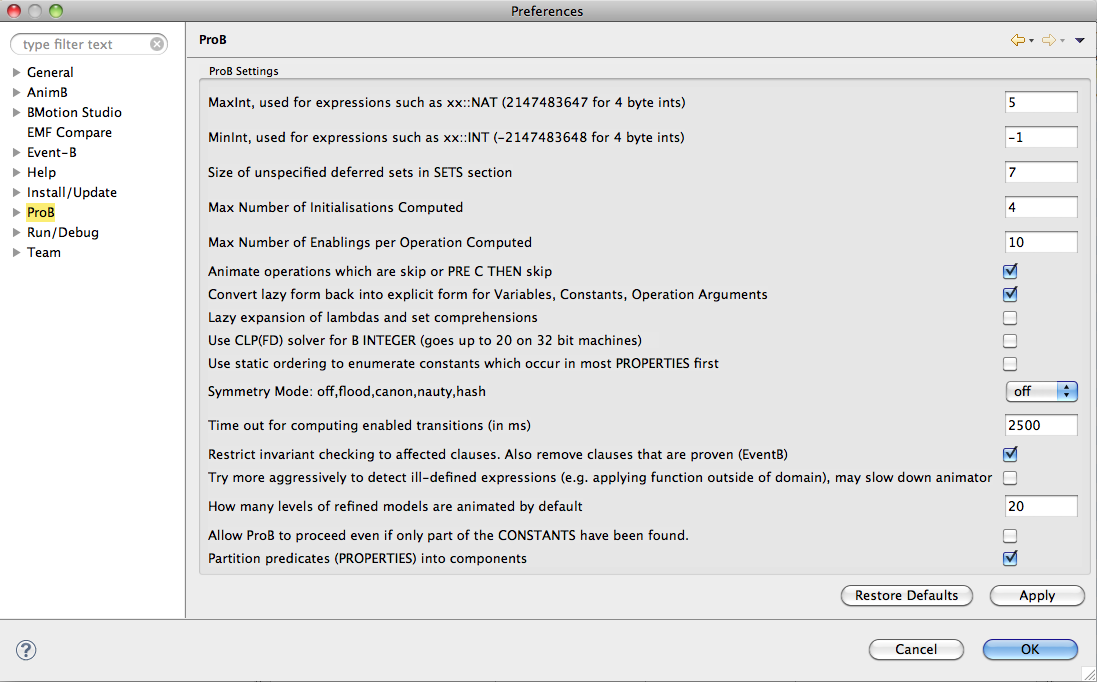
We explain the most important preferences below.
Minint and Maxint
We first explain the first two entries in the screenshot above. Within classical B this provides the range for the implementable integer type. In Rodin, there are only the mathematical integers, and there is no MININT or MAXINT constant. However, this preference will be used by ProB if it cannot determine the value of an integer variable in order to know in which range it should be enumerated.
Size of unspecified sets (carrier sets)
This is the third entry in the screen shot above. ProB requires all carrier sets to be finite and ProB has to know the cardinality before starting the animation or model checking.
Some sets are explicitly enumerated, and thus finite. ProB will use this to infer the correct cardinality.
For the other sets, ProB will try to chose a cardinality. If the axioms of a context contain explicit predicates about the cardinality, such as card(S)=4, then this value will be used. You can also use card(S)<n to specify a maximum cardinality, or card(S)>n to specify a minimum cardinality. If no cardinality is specified, ProB will use the default size provided in the preferences dialog (the entry "Size of unspecified deferred sets...").
Using contexts for ProB animation
Note that you can create a new context with those axioms just for animation or model checking with ProB. For this you can simply right-click on the context and use the Rodin command "EXTEND". For example, in Camille syntax such a context could look like:
context c1_prob extends c1 axioms @prob_axm card(S) = 3 end
After that you can also refine the model you want to animate by right-clicking on it and using the Rodin command "REFINE", and then add the new context to the seen context list:
machine m0_prob refines m0 sees c0 c1_prob
Here the machine m0_prob and c1_prob play the role of configuration files for the animation. You can also add additional axioms in c1_prob to force ProB to use a specific valuation of your constants.
If ProB cannot infer the size of a carrier set; it will use the default value provided in the "Size of unspecified sets" preference.
Note that for complicated machines it can be tricky to set up the cardinalities of the carrier sets correctly. For example, if you have an axiom f : A -->> B, then the cardinality of A must be greater or equal to the cardinality of B. We are working on an automated analysis for detecting the correct cardinalities of the carrier sets automatically.
Transforming deferred carrier sets into enumerated sets
Instead of providing a cardinality you can also transform a deferred set into an enumerated set, i.e., provided an enumeration of all its elements. Here is how you would instantiate S to be a set containing the three elements named a,b,c:
context c1_prob extends c1
constants a,b,c
axioms
@prob_axm partition(S,{a},{b},{c})
end