Nine Prisoners: Difference between revisions
No edit summary |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
<em> "So in the spirit of Kirkman, we will leave the gentle reader with another brainteaser, a slight variation on the schoolgirl puzzle devised in 1917 by the British puzzle aficionado Henry Ernest Dudeney and later popularized by Martin Gardner: Nine prisoners are taken outdoors for exercise in rows of three, with each adjacent pair of prisoners linked by handcuffs, on each of the six weekdays (back in Dudeney’s less enlightened times, Saturday was still a weekday). Can the prisoners be arranged over the course of the six days so that each pair of prisoners shares handcuffs exactly once?" </em> | <em> "So in the spirit of Kirkman, we will leave the gentle reader with another brainteaser, a slight variation on the schoolgirl puzzle devised in 1917 by the British puzzle aficionado Henry Ernest Dudeney and later popularized by Martin Gardner: Nine prisoners are taken outdoors for exercise in rows of three, with each adjacent pair of prisoners linked by handcuffs, on each of the six weekdays (back in Dudeney’s less enlightened times, Saturday was still a weekday). Can the prisoners be arranged over the course of the six days so that each pair of prisoners shares handcuffs exactly once?" </em> | ||
Other links to this puzzle are [https://link.springer.com/content/pdf/10.1007/978-0-387-30389-5_8 | Other links to this puzzle are [https://link.springer.com/content/pdf/10.1007/978-0-387-30389-5_8 Dinner Guests, Schoolgirls, and Handcuffed Prisoners] | ||
and [https://martin-gardner.org/MGSAindex.html May 1980 column: What unifies dinner guests, strolling schoolgirls and handcuffed prisoners?] | and [https://martin-gardner.org/MGSAindex.html May 1980 column: What unifies dinner guests, strolling schoolgirls and handcuffed prisoners?] | ||
An encoding of this puzzle in B is relatively straightforward, thanks to the use of sets, sequences and permutations and universal quantification. | An encoding of this puzzle in B is relatively straightforward, thanks to the use of sets, sequences and permutations and universal quantification. | ||
| Line 86: | Line 86: | ||
Details about the use of this visualization feature can be found in the [[Graphical_Visualization]] page of the manual. | Details about the use of this visualization feature can be found in the [[Graphical_Visualization]] page of the manual. | ||
Here is a another version, also containing a VisB visualisation | |||
and using an encoding where ProB is more efficient: | |||
<pre> | |||
MACHINE NinePrisoners_v4 | |||
/* | |||
From | |||
http://www.wired.com/2015/06/answer-150-year-old-math-conundrum-brings-mystery/ : | |||
"So in the spirit of Kirkman, we will leave the gentle reader with another brainteaser, a slight variation on the schoolgirl puzzle devised in 1917 by the British puzzle aficionado Henry Ernest Dudeney and later popularized by Martin Gardner: | |||
Nine prisoners are taken outdoors for exercise in rows of three, with each adjacent pair of prisoners linked by handcuffs, on each of the six weekdays (back in Dudeney’s less enlightened times, Saturday was still a weekday). | |||
Can the prisoners be arranged over the course of the six days so that each pair of prisoners shares handcuffs exactly once?" | |||
*/ | |||
DEFINITIONS | |||
Prisoners == 1..9; | |||
Days == 6; /* 19 seconds for 6 days */ | |||
Cuffs == {1,2, 4,5, 7,8 }; | |||
share(day,cuff) == {arrange(day,cuff),arrange(day,cuff+1)}; | |||
share1(day,cuff) == (arrange(day,cuff),arrange(day,cuff+1)); // share as ordered pair rather than set | |||
share2(day,cuff) == (arrange(day,cuff+1),arrange(day,cuff)); // pair in other order | |||
SET_PREF_TIME_OUT == 3800*2**Days; | |||
SET_PREF_CLPFD == TRUE; | |||
SET_PREF_SMT == TRUE; // with FALSE it takes 33 instead of 19 secs for 6 days | |||
SET_PREF_TRY_FIND_ABORT == FALSE; | |||
SET_PREF_PERFORMANCE_INFO == TRUE; | |||
SET_PREF_TRACE_INFO == FALSE; | |||
SET_PREF_MAX_INITIALISATIONS == 3; | |||
ANIMATION_FUNCTION == | |||
{r,c,i| r:1..Days & c:1..3 & i = arrange(r,c) } \/ | |||
{r,c,i| r:1..Days & c:5..7 & i = arrange(r,c-1) } \/ | |||
{r,c,i| r:1..Days & c:9..11 & i = arrange(r,c-2) }; | |||
ANIMATION_FUNCTION_DEFAULT == {r,c,i| r:1..Days & c:1..11 & i = 0 }; | |||
ANIMATION_IMG0 == "images/Prisoner_0.gif"; | |||
ANIMATION_IMG1 == "images/Prisoner_1.gif"; | |||
ANIMATION_IMG2 == "images/Prisoner_2.gif"; | |||
ANIMATION_IMG3 == "images/Prisoner_3.gif"; | |||
ANIMATION_IMG4 == "images/Prisoner_4.gif"; | |||
ANIMATION_IMG5 == "images/Prisoner_5.gif"; | |||
ANIMATION_IMG6 == "images/Prisoner_6.gif"; | |||
ANIMATION_IMG7 == "images/Prisoner_7.gif"; | |||
ANIMATION_IMG8 == "images/Prisoner_8.gif"; | |||
ANIMATION_IMG9 == "images/Prisoner_9.gif"; | |||
WID == 20; VISB_JSON_FILE == ""; VISB_SVG_BOX == rec(width:(2+card(Prisoners))*WID, height:(Days+2)*WID); | |||
pcolor == ["red","blue","green","yellow","purple","gray","orange","white","cyan"]; | |||
VISB_SVG_OBJECTS1 == {d,p•d:1..Days & p:Prisoners | | |||
rec(svg_class:"rect", x:p*WID, y:d*WID, width:WID-2, height:WID, | |||
fill:pcolor(arrange(d,p)), stroke:"black", | |||
title:```Day ${d} for Prisoner ${p}```)}; | |||
SYMMETRY1 == !i.(i:Prisoners => arrange(1,i) = i); // starting row fixed for day 1 | |||
SYMMETRY2 == !d.(d:1..Days => | |||
!c.(c:Prisoners & c mod 3 = 1 // {1, 4, 7} ; symmetry breaking inside each triple | |||
=> arrange(d,c) < arrange(d,c+2))); | |||
SYMMETRY3 == !d.(d:1..Days => | |||
!c.(c:{1,3} => arrange(d,c) < arrange(d,c+3))) // symmetry breaking of the triples | |||
CONSTANTS arrange | |||
PROPERTIES | |||
arrange : (1..Days)*Prisoners --> Prisoners & | |||
/* permutation requirement: */ | |||
!i.(i:1..Days => card({arrange(i,1),arrange(i,2),arrange(i,3), | |||
arrange(i,4),arrange(i,5),arrange(i,6), | |||
arrange(i,7),arrange(i,8),arrange(i,9)}) = 9) & | |||
/* symmetry breaking */ | |||
SYMMETRY1 & | |||
SYMMETRY2 & | |||
SYMMETRY3 & | |||
/* the constraint proper */ | |||
!(c,d).(c:Cuffs & d:2..Days => | |||
!(c1,d1).(d1: 1..(Days-1) & d1 < d & c1:Cuffs => | |||
// !(c1,d1).(d1<d & d1>0 & c1:Cuffs => | |||
(share1(d,c) /= share1(d1,c1) & | |||
share1(d,c) /= share2(d1,c1)) | |||
) | |||
) // & observe(arrange) // observe((arrange(2),arrange(3),arrange(4),arrange(5),arrange(6),arrange)) | |||
ASSERTIONS | |||
!i.(i:1..Days => card({j•j:Prisoners|arrange(i,j)}) = 9); // this is more generic, but slower than the next version: | |||
OPERATIONS | |||
r <-- Neighbours(i) = PRE i:Prisoners THEN /* compute for every day the neighbours of i */ | |||
r := %d.(d:1..Days | | |||
UNION(x,c).( x:Prisoners & c:Cuffs & i: share(d,c)| share(d,c) \ {i}) | |||
) END | |||
END | |||
</pre> | |||
Latest revision as of 13:05, 30 April 2025
An article in Quanta magazine mentions the following puzzle by Dudeney and popularized by Martin Gardner:
"So in the spirit of Kirkman, we will leave the gentle reader with another brainteaser, a slight variation on the schoolgirl puzzle devised in 1917 by the British puzzle aficionado Henry Ernest Dudeney and later popularized by Martin Gardner: Nine prisoners are taken outdoors for exercise in rows of three, with each adjacent pair of prisoners linked by handcuffs, on each of the six weekdays (back in Dudeney’s less enlightened times, Saturday was still a weekday). Can the prisoners be arranged over the course of the six days so that each pair of prisoners shares handcuffs exactly once?"
Other links to this puzzle are Dinner Guests, Schoolgirls, and Handcuffed Prisoners and May 1980 column: What unifies dinner guests, strolling schoolgirls and handcuffed prisoners?
An encoding of this puzzle in B is relatively straightforward, thanks to the use of sets, sequences and permutations and universal quantification. To improve the performance, symmetry reductions were added by hand in the model below. The constant arrange contains the solution to our puzzle: the arrangement of the prisoners for every working day from 1 to Days.
MACHINE NinePrisoners
DEFINITIONS
Prisoners == 1..9;
Days == 6;
Cuffs == {1,2, 4,5, 7,8 };
share(day,cuff) == {arrange(day)(cuff),arrange(day)(cuff+1)}
CONSTANTS arrange
PROPERTIES
/* typing + permutation requirement */
arrange : (1..Days) --> perm(Prisoners) &
/* symmetry breaking */
arrange(1) = %i.(i:Prisoners|i) &
!d.(d:1..Days =>
!c.(c:Prisoners & c mod 3 = 1 => arrange(d)(c) < arrange(d)(c+2))) &
!d.(d:1..Days =>
!c.(c:{1,3} => arrange(d)(c) < arrange(d)(c+3)))
&
/* the constraint proper */
!(c,d).(c:Cuffs & d:2..Days =>
!(c1,d1).(d1<d & d1>0 & c1:Cuffs =>
share(d,c) /= share(d1,c1))
)
END
The solving time using ProB on a MacBook Air is as follows: for Days == 4: 0.08 seconds, for Days==5: 0.20 seconds, for Days == 6: 80 seconds (i.e., the complete puzzle).
Simple Graphical Visualization
To generate a simple graphical visualization of the solutions found by ProB, one needs to add a definition for the animation function, e.g., as follows:
ANIMATION_FUNCTION ==
{r,c,i| r:1..Days & c:1..3 & i = arrange(r)(c) } \/
{r,c,i| r:1..Days & c:5..7 & i = arrange(r)(c-1) } \/
{r,c,i| r:1..Days & c:9..11 & i = arrange(r)(c-2) };
ANIMATION_FUNCTION_DEFAULT == {r,c,i| r:1..Days & c:1..11 & i = " " }
This gives rise to the following visualisation:
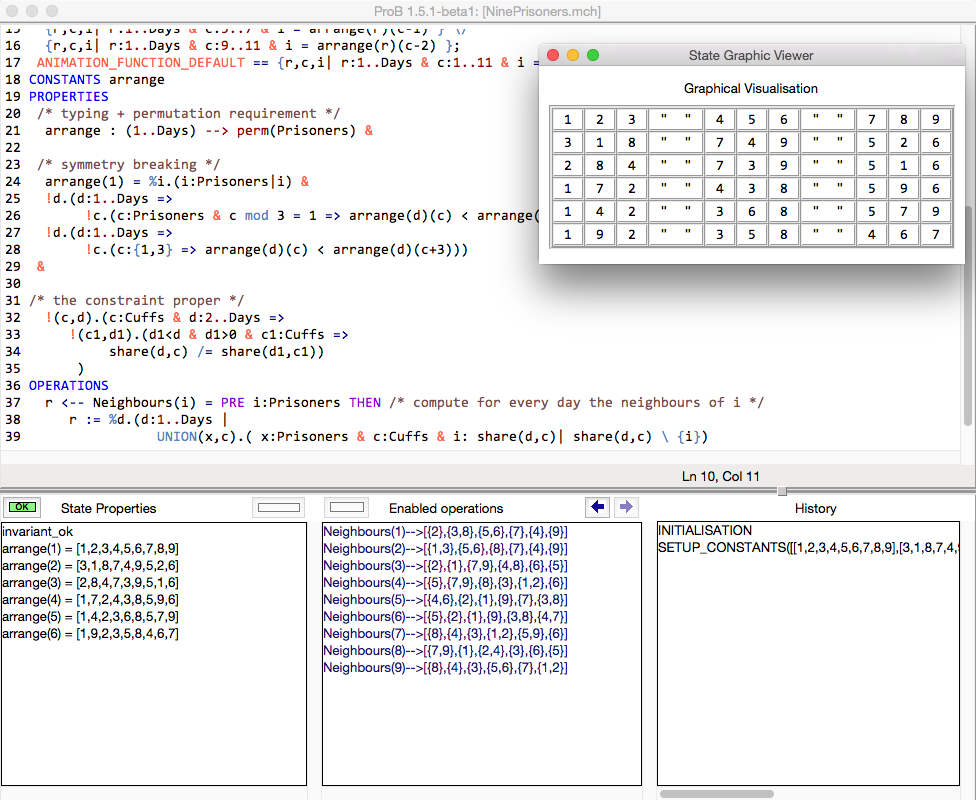
As can be seen in the screenshot, we have also added an operation to inspect the solution computed by ProB:
OPERATIONS
r <-- Neighbours(i) = PRE i:Prisoners THEN /* compute for every day the neighbours of i */
r := %d.(d:1..Days |
UNION(x,c).( x:Prisoners & c:Cuffs & i: share(d,c)| share(d,c) \ {i})
) END
Adding graphical visualization
To add a better graphical visualization one needs to generate 10 pictures (in GIF format). I generate these using OmniGraffle. In the DEFINITIONS section of the B machine above, you then simply have to add the following (and remove the definition of ANIMATION_FUNCTION_DEFAULT from above):
ANIMATION_FUNCTION_DEFAULT == {r,c,i| r:1..Days & c:1..11 & i = 0 };
ANIMATION_IMG0 == "images/Prisoner_0.gif";
ANIMATION_IMG1 == "images/Prisoner_1.gif";
ANIMATION_IMG2 == "images/Prisoner_2.gif";
ANIMATION_IMG3 == "images/Prisoner_3.gif";
ANIMATION_IMG4 == "images/Prisoner_4.gif";
ANIMATION_IMG5 == "images/Prisoner_5.gif";
ANIMATION_IMG6 == "images/Prisoner_6.gif";
ANIMATION_IMG7 == "images/Prisoner_7.gif";
ANIMATION_IMG8 == "images/Prisoner_8.gif";
ANIMATION_IMG9 == "images/Prisoner_9.gif"
This gives rise to the following graphical visualization of the first solution found by ProB:

Details about the use of this visualization feature can be found in the Graphical_Visualization page of the manual.
Here is a another version, also containing a VisB visualisation and using an encoding where ProB is more efficient:
MACHINE NinePrisoners_v4
/*
From
http://www.wired.com/2015/06/answer-150-year-old-math-conundrum-brings-mystery/ :
"So in the spirit of Kirkman, we will leave the gentle reader with another brainteaser, a slight variation on the schoolgirl puzzle devised in 1917 by the British puzzle aficionado Henry Ernest Dudeney and later popularized by Martin Gardner:
Nine prisoners are taken outdoors for exercise in rows of three, with each adjacent pair of prisoners linked by handcuffs, on each of the six weekdays (back in Dudeney’s less enlightened times, Saturday was still a weekday).
Can the prisoners be arranged over the course of the six days so that each pair of prisoners shares handcuffs exactly once?"
*/
DEFINITIONS
Prisoners == 1..9;
Days == 6; /* 19 seconds for 6 days */
Cuffs == {1,2, 4,5, 7,8 };
share(day,cuff) == {arrange(day,cuff),arrange(day,cuff+1)};
share1(day,cuff) == (arrange(day,cuff),arrange(day,cuff+1)); // share as ordered pair rather than set
share2(day,cuff) == (arrange(day,cuff+1),arrange(day,cuff)); // pair in other order
SET_PREF_TIME_OUT == 3800*2**Days;
SET_PREF_CLPFD == TRUE;
SET_PREF_SMT == TRUE; // with FALSE it takes 33 instead of 19 secs for 6 days
SET_PREF_TRY_FIND_ABORT == FALSE;
SET_PREF_PERFORMANCE_INFO == TRUE;
SET_PREF_TRACE_INFO == FALSE;
SET_PREF_MAX_INITIALISATIONS == 3;
ANIMATION_FUNCTION ==
{r,c,i| r:1..Days & c:1..3 & i = arrange(r,c) } \/
{r,c,i| r:1..Days & c:5..7 & i = arrange(r,c-1) } \/
{r,c,i| r:1..Days & c:9..11 & i = arrange(r,c-2) };
ANIMATION_FUNCTION_DEFAULT == {r,c,i| r:1..Days & c:1..11 & i = 0 };
ANIMATION_IMG0 == "images/Prisoner_0.gif";
ANIMATION_IMG1 == "images/Prisoner_1.gif";
ANIMATION_IMG2 == "images/Prisoner_2.gif";
ANIMATION_IMG3 == "images/Prisoner_3.gif";
ANIMATION_IMG4 == "images/Prisoner_4.gif";
ANIMATION_IMG5 == "images/Prisoner_5.gif";
ANIMATION_IMG6 == "images/Prisoner_6.gif";
ANIMATION_IMG7 == "images/Prisoner_7.gif";
ANIMATION_IMG8 == "images/Prisoner_8.gif";
ANIMATION_IMG9 == "images/Prisoner_9.gif";
WID == 20; VISB_JSON_FILE == ""; VISB_SVG_BOX == rec(width:(2+card(Prisoners))*WID, height:(Days+2)*WID);
pcolor == ["red","blue","green","yellow","purple","gray","orange","white","cyan"];
VISB_SVG_OBJECTS1 == {d,p•d:1..Days & p:Prisoners |
rec(svg_class:"rect", x:p*WID, y:d*WID, width:WID-2, height:WID,
fill:pcolor(arrange(d,p)), stroke:"black",
title:```Day ${d} for Prisoner ${p}```)};
SYMMETRY1 == !i.(i:Prisoners => arrange(1,i) = i); // starting row fixed for day 1
SYMMETRY2 == !d.(d:1..Days =>
!c.(c:Prisoners & c mod 3 = 1 // {1, 4, 7} ; symmetry breaking inside each triple
=> arrange(d,c) < arrange(d,c+2)));
SYMMETRY3 == !d.(d:1..Days =>
!c.(c:{1,3} => arrange(d,c) < arrange(d,c+3))) // symmetry breaking of the triples
CONSTANTS arrange
PROPERTIES
arrange : (1..Days)*Prisoners --> Prisoners &
/* permutation requirement: */
!i.(i:1..Days => card({arrange(i,1),arrange(i,2),arrange(i,3),
arrange(i,4),arrange(i,5),arrange(i,6),
arrange(i,7),arrange(i,8),arrange(i,9)}) = 9) &
/* symmetry breaking */
SYMMETRY1 &
SYMMETRY2 &
SYMMETRY3 &
/* the constraint proper */
!(c,d).(c:Cuffs & d:2..Days =>
!(c1,d1).(d1: 1..(Days-1) & d1 < d & c1:Cuffs =>
// !(c1,d1).(d1<d & d1>0 & c1:Cuffs =>
(share1(d,c) /= share1(d1,c1) &
share1(d,c) /= share2(d1,c1))
)
) // & observe(arrange) // observe((arrange(2),arrange(3),arrange(4),arrange(5),arrange(6),arrange))
ASSERTIONS
!i.(i:1..Days => card({j•j:Prisoners|arrange(i,j)}) = 9); // this is more generic, but slower than the next version:
OPERATIONS
r <-- Neighbours(i) = PRE i:Prisoners THEN /* compute for every day the neighbours of i */
r := %d.(d:1..Days |
UNION(x,c).( x:Prisoners & c:Cuffs & i: share(d,c)| share(d,c) \ {i})
) END
END