Rules-DSL: Difference between revisions
Jan Gruteser (talk | contribs) |
Jan Gruteser (talk | contribs) |
||
| (42 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Rules DSL == | == B-Rules DSL == | ||
The B Rules domain-specific language mainly provides operations for data validation. <em>Rules</em> allow checking for expected properties, while <em>computations</em> can be used to define and compute variables based on the successful execution of certain rules. Furthermore you can use <em>functions</em> to compute values multiple times depending on different inputs. | The B-Rules domain-specific language (B-Rules DSL) mainly provides operations for data validation. <em>Rules</em> allow checking for expected properties, while <em>computations</em> can be used to define and compute variables based on the successful execution of certain rules. Furthermore you can use <em>functions</em> to compute values multiple times depending on different inputs. | ||
===Setting up a Rules Machine=== | ===Setting up a Rules Machine=== | ||
| Line 9: | Line 9: | ||
REFERENCES list of rules machines | REFERENCES list of rules machines | ||
</pre> | </pre> | ||
The latter allows inclusion of other rules machines. Below, | The latter allows the inclusion of other rules machines and ordinary B machines that contain only constants, but not yet any other B machines. Below, <code>SETS</code>, <code>DEFINITIONS</code>, <code>PROPERTIES</code> or <code>CONSTANTS</code> can be used as in a normal B machine. Note that <code>VARIABLES</code> are not allowed as they are set by rule based computations. | ||
====Rules==== | ====Rules==== | ||
| Line 24: | Line 24: | ||
END | END | ||
</pre> | </pre> | ||
If a rule depends on other rules, it can only be executed if the specified rules have been successfully checked, i.e. their corresponding variables <code>rule_name</code> have the value <code>SUCCESS</code>. In addition, rules can depend on computations. In this case, a rule is enabled when the specified | The specified <code>rule_name</code> will be the name of the operation and variable storing the result. | ||
If a rule depends on other rules, it can only be executed if the specified rules have been successfully checked, i.e. their corresponding variables <code>rule_name</code> have the value <code>SUCCESS</code>. In addition, rules can depend on computations. In this case, a rule is enabled when the specified computations have been executed. If a rule uses variables that are defined by computations, the corresponding computations are added implicitly as dependencies and do not have to be declared explicitly. Any other preconditions can be specified as an <code>ACTIVATION</code> predicate. An important note is that the activation predicate is evaluated statically at initialisation and disables the rule if the predicate is false. Activation predicates and dependencies can be omitted if they are not needed. | |||
To use different error types (for example, if a rule has multiple bodies and it is necessary to distinguish between them), the number of error types has to be declared in the rule header. | |||
Error types are also optional. | |||
The actual rule conditions are specified within the body of a rule, which contains the name and the preconditions. | |||
A rule succeeds if and only if all rule conditions in its body are satisfied. | |||
There are two constructs for rule bodies that can be used arbitrarily often in the body of a rule. | |||
The following is formulated in a positive way, i.e. the execution of the rule leads to <code>SUCCESS</code> if the conditions in the <code>EXPECT</code>-part are fulfilled. | The following is formulated in a positive way, i.e. the execution of the rule leads to <code>SUCCESS</code> if the conditions in the <code>EXPECT</code>-part are fulfilled. | ||
In contrast to the <code>RULE_FAIL</code> body (see below), in <code>RULE_FORALL</code> you can obtain success messages (such as counter examples) for successful applications of the rule. | |||
<pre> | <pre> | ||
RULE_FORALL | RULE_FORALL | ||
| Line 39: | Line 44: | ||
ERROR_TYPE | ERROR_TYPE | ||
number encoding error type, must be in range of error types | number encoding error type, must be in range of error types | ||
ON_SUCCESS | |||
STRING_FORMAT("errorMessage ~w", identifier from list) or | |||
```${identifier from list}``` (template string) | |||
COUNTEREXAMPLE | COUNTEREXAMPLE | ||
STRING_FORMAT("errorMessage ~w", identifier from list) | STRING_FORMAT("errorMessage ~w", identifier from list) or | ||
```${identifier from list}``` (template string) | |||
END | END | ||
</pre> | </pre> | ||
Alternatively, | Alternatively, a negated rule can be formulated. Here the execution of the rule results in <code>FAIL</code> if the conditions in the <code>WHEN</code>-part are fulfilled. | ||
<pre> | <pre> | ||
RULE_FAIL | RULE_FAIL | ||
| Line 57: | Line 66: | ||
Counterexamples are of the type <code>INTEGER <-> STRING</code>. The integer contains the error type, while the string contains the message of the counterexample. | Counterexamples are of the type <code>INTEGER <-> STRING</code>. The integer contains the error type, while the string contains the message of the counterexample. | ||
Also valid for the rules header | Also valid for the rules header are: | ||
<pre> | <pre> | ||
RULEID id | |||
CLASSIFICATION identifier | CLASSIFICATION identifier | ||
TAGS identifier | TAGS identifier | ||
</pre> | </pre> | ||
The <code>CLASSIFICATION</code> keyword can be used to group the rules in the [[#Rule_Validation_in_ProB2-UI|HTML validation report]] according to their classification. | |||
====Computations==== | ====Computations==== | ||
Computations can be used to | Computations can be used to define variables. As for rules, their activation can depend on further rules, computations or any other predicate specified as an activation condition. Again, the activation condition is evaluated at initialisation and sets the computation status variable to <code>COMPUTATION_DISABLED</code> if the predicate is false. Furthermore, a <code>DUMMY_VALUE</code> can be set, which initialises the variable with the specified value instead of the empty set before execution of the computation. This mechanism implies that each variable defined by a computation must be a set of type <code>POW(S)</code> for any <code>TYPE</code> <code>S</code> (note: the <tt>TYPE</tt> section is optional since ProB parser version 2.15.1). A computation can be replaced by a previously defined computation if it sets the same variable (of the same type) by using <code>REPLACES</code>. The general syntax for computations is: | ||
<pre> | <pre> | ||
COMPUTATION computation_name | COMPUTATION computation_name | ||
| Line 80: | Line 90: | ||
END | END | ||
</pre> | </pre> | ||
Activation predicates, dependencies, and also the dummy value can be omitted if they are not needed. After the execution of a computation, the value of the corresponding variable <code>computation_name</code> is changed from <code>NOT_EXECUTED</code> to <code>EXECUTED</code> and the variable <code>variable_name</code> has the value \texttt{VALUE}. For related computations, it may be useful to use multiple <code>DEFINE</code> blocks in one computation. | |||
Separated by <code>;</code>, the body of a computation can contain any number of variable definitions. | |||
====Functions==== | ====Functions==== | ||
Functions can be called from any rules machine that references the machine containing the function. Depending on input parameters that must | Functions can be called from any rules machine that references the machine containing the function. Depending on input parameters that must fulfil specified preconditions, the functions returns output value(s) that must fulfil optional postconditions. In the body, any B statement can be used to (sequentially) compute the output value. | ||
<pre> | <pre> | ||
FUNCTION output <-- function_name(list of input parameters) | FUNCTION output <-- function_name(list of input parameters) | ||
| Line 99: | Line 108: | ||
====Additional Syntax==== | ====Additional Syntax==== | ||
There are some useful | There are some useful predicates available in rules machines that can be used to check the success or failure of rules. It is also possible to check whether a certain error type was returned by a rule. These are: | ||
<ul> | <ul> | ||
<li><code>SUCCEEDED_RULE(rule1)</code>: TRUE, if the check of rule1 succeeded</li> | <li><code>SUCCEEDED_RULE(rule1)</code>: TRUE, if the check of rule1 succeeded</li> | ||
<li><code>SUCCEEDED_RULE_ERROR_TYPE(rule1,1)</code>: TRUE, if the check of rule1 | <li><code>SUCCEEDED_RULE_ERROR_TYPE(rule1,1)</code>: TRUE, if the check of rule1 did not fail with error type 1</li> | ||
<li><code>GET_RULE_COUNTEREXAMPLES(rule1)</code>: set of counterexamples of rule1</li> | <li><code>GET_RULE_COUNTEREXAMPLES(rule1)</code>: set of counterexamples of rule1</li> | ||
<li><code>FAILED_RULE(rule1)</code>: TRUE, if the check of rule1 failed</li> | <li><code>FAILED_RULE(rule1)</code>: TRUE, if the check of rule1 failed</li> | ||
<li><code>FAILED_RULE_ERROR_TYPE(rule1,2)</code>: TRUE, if | <li><code>FAILED_RULE_ERROR_TYPE(rule1,2)</code>: TRUE, if check of rule1 failed with error type 2</li> | ||
<li><code>FAILED_RULE_ALL_ERROR_TYPES(rule1)</code>: TRUE, if the check of rule1 failed with all possible error types for rule1</li> | <li><code>FAILED_RULE_ALL_ERROR_TYPES(rule1)</code>: TRUE, if the check of rule1 failed with all possible error types for rule1</li> | ||
<li><code>NOT_CHECKED_RULE(rule1)</code>: TRUE, if rule1 has not yet been checked</li> | <li><code>NOT_CHECKED_RULE(rule1)</code>: TRUE, if rule1 has not yet been checked</li> | ||
<li><code>DISABLED_RULE(rule1)</code>: TRUE, if rule1 is disabled ( | <li><code>DISABLED_RULE(rule1)</code>: TRUE, if rule1 is disabled (its preconditions are not fulfilled)</li> | ||
</ul> | </ul> | ||
Another | Another functionality of rules machines are FOR-loops. Their syntax is: | ||
<pre> | <pre> | ||
FOR variable(s) IN set | FOR variable(s) IN set | ||
| Line 130: | Line 139: | ||
</pre> | </pre> | ||
This rule always fails and returns <code>{1 |-> "example_rule_fail: 2", 1 |-> "example_rule_fail: 3"}</code>. | This rule always fails and returns <code>{1 |-> "example_rule_fail: 2", 1 |-> "example_rule_fail: 3"}</code>. | ||
===Rule Validation in ProB2-UI=== | |||
Rule validation has been integrated into the ProB2-UI since version 1.2.2 (not yet released). | |||
It allows convenient execution of rules and computations together with a graphical representation of the results. | |||
Rules are grouped by their classification and can be additionally filtered by their name, ID, or tags. | |||
The results can also be exported as an HTML report. | |||
In addition, dependencies of rules and computations can be visualised as a graph either for all operations or for just one operation (the HTML report and the dependency graph are generated by the ProB Java API and can also be created without ProB2-UI). | |||
[[File:ProB2 UI Rules View.png|500px|ProB2-UI Rules View]] | |||
===Rule Validation with probcli=== | |||
The probcli recognises the option <code>-rule_report <file></code> which generates the same HTML/XML validation report as in ProB2-UI for the current animation state. | |||
The provided file extension is used to determine whether the HTML or the XML version of the report is generated. | |||
To validate all rules, use this option in combination with <code>-execute_all</code>. | |||
There is also a dot visualisation command "rule_dependency graph" that can be used to create a graph of the dependencies of rules and computations (including results of the current state); example call: | |||
<pre>probcli myMch.mch -execute_all -rule_report myReport.html -dot "rule_dependency_graph" myGraph.pdf</pre> | |||
All three export options are also available in ProB Tcl/Tk via the visualization menu. | |||
Using the special definition <code>RULE_REPORT_CONTEXT</code> you can include context information about the check in the report (of the type <tt>STRING</tt>), e.g. the file name of a validated XML file. | |||
===Use Rules for Data Validation=== | ===Use Rules for Data Validation=== | ||
The concept of rule validation can be used to validate data from external sources such as CSV or XML files and load the validated data into ProB by successive computations. | |||
For an XML file, this could look as follows: | |||
<pre> | <pre> | ||
RULES_MACHINE XML_import | RULES_MACHINE XML_import | ||
| Line 164: | Line 192: | ||
END; | END; | ||
</pre> | </pre> | ||
===Internal Representation=== | |||
Each rules machine is internally translated to an ordinary B machine, which can be accessed as its internal representation. | |||
Consider the following example rule: | |||
<pre> | |||
RULE rule1 BODY RULE_FAIL WHEN bfalse COUNTEREXAMPLE "" END END; | |||
COMPUTATION comp1 | |||
BODY | |||
DEFINE x | |||
TYPE POW(INTEGER) | |||
VALUE 1..10 | |||
END | |||
END; | |||
RULE rule2 | |||
DEPENDS_ON_RULE rule1 | |||
// DEPENDS_ON_COMPUTATION comp1 | |||
BODY | |||
RULE_FORALL i | |||
WHERE i : 1..10 | |||
EXPECT i > 5 | |||
COUNTEREXAMPLE STRING_FORMAT("~w <= 5", i) | |||
END | |||
END | |||
</pre> | |||
Its internal representation in classical B is the following: | |||
<pre> | |||
`$RESULT`,`$COUNTEREXAMPLES` <-- rule1 = | |||
SELECT | |||
rule1 = "NOT_CHECKED" | |||
THEN | |||
rule1,`$RESULT`,`$COUNTEREXAMPLES` := "SUCCESS","SUCCESS",{} | |||
END; | |||
comp1 = | |||
SELECT | |||
comp1 = "NOT_EXECUTED" | |||
THEN | |||
x,comp1 := FORCE(1 .. 10),"EXECUTED" | |||
END; | |||
`$RESULT`,`$COUNTEREXAMPLES` <-- rule2 = | |||
SELECT | |||
rule2 = "NOT_CHECKED" | |||
& rule1 = "SUCCESS" | |||
& comp1 = "EXECUTED" | |||
THEN | |||
rule2,`$RESULT`,`$COUNTEREXAMPLES` := "SUCCESS","SUCCESS",{} ; | |||
VAR `$ResultTuple`,`$ResultStrings` | |||
IN | |||
`$ResultTuple` := FORCE({i|i : x & not(i > 5)}) ; | |||
`$ResultStrings` := FORCE({`$String`|`$String` : STRING & #i.(i : `$ResultTuple` & `$String` = FORMAT_TO_STRING("~w <= 5",[TO_STRING(i)]))}); | |||
rule2_Counterexamples := rule2_Counterexamples \/ {1} * `$ResultStrings` ; | |||
IF `$ResultTuple` /= {} THEN | |||
rule2,`$RESULT`,`$COUNTEREXAMPLES` := "FAIL","FAIL",rule2_Counterexamples | |||
END | |||
END | |||
END | |||
</pre> | |||
Observe that the implicit dependency of rule2 on comp1 (rule2 uses its variable x) is detected automatically without explicit declaration. | |||
===Include Rules Machines into other Projects=== | ===Include Rules Machines into other Projects=== | ||
Currently, it is not possible to include rules machines directly into any other machines. Instead, use the rules machine at the top of the hierarchy (of the rules project) and save the internal generated machine as <code>.mch</code>. After changing the machine name accordingly, the rules can be included and used via this machine. | Currently, it is not possible to include rules machines directly into any other machines. Instead, use the rules machine at the top of the hierarchy (of the rules project) and save the internal generated machine as <code>.mch</code>-file. After changing the machine name accordingly, the rules can be included and used via this machine. | ||
Note that in this case it is not possible to perform Rules-DSL specific methods of the ProB Java API (like detailed information about rule results). | |||
Latest revision as of 17:06, 30 April 2025
B-Rules DSL
The B-Rules domain-specific language (B-Rules DSL) mainly provides operations for data validation. Rules allow checking for expected properties, while computations can be used to define and compute variables based on the successful execution of certain rules. Furthermore you can use functions to compute values multiple times depending on different inputs.
Setting up a Rules Machine
Rules machines are stored in .rmch-files. The general setup for the machine header is:
RULES_MACHINE machine_name REFERENCES list of rules machines
The latter allows the inclusion of other rules machines and ordinary B machines that contain only constants, but not yet any other B machines. Below, SETS, DEFINITIONS, PROPERTIES or CONSTANTS can be used as in a normal B machine. Note that VARIABLES are not allowed as they are set by rule based computations.
Rules
Rules can be defined in the OPERATIONS-section of a rules machine. Depending on whether the expectations are met, a rule returns SUCCESS or FAIL. If a rule fails, additionally provided string messages are returned as counterexamples.
In the B Rules-DSL a rule has the following structure:
RULE rule_name // will be the name of the operation and variable storing the result
DEPENDS_ON_RULE list of rules
DEPENDS_ON_COMPUTATION list of computations
ACTIVATION predicate
ERROR_TYPES positive number of error types
BODY
arbitrarily many rule bodys (see below)
END
The specified rule_name will be the name of the operation and variable storing the result.
If a rule depends on other rules, it can only be executed if the specified rules have been successfully checked, i.e. their corresponding variables rule_name have the value SUCCESS. In addition, rules can depend on computations. In this case, a rule is enabled when the specified computations have been executed. If a rule uses variables that are defined by computations, the corresponding computations are added implicitly as dependencies and do not have to be declared explicitly. Any other preconditions can be specified as an ACTIVATION predicate. An important note is that the activation predicate is evaluated statically at initialisation and disables the rule if the predicate is false. Activation predicates and dependencies can be omitted if they are not needed.
To use different error types (for example, if a rule has multiple bodies and it is necessary to distinguish between them), the number of error types has to be declared in the rule header. Error types are also optional.
The actual rule conditions are specified within the body of a rule, which contains the name and the preconditions.
A rule succeeds if and only if all rule conditions in its body are satisfied.
There are two constructs for rule bodies that can be used arbitrarily often in the body of a rule.
The following is formulated in a positive way, i.e. the execution of the rule leads to SUCCESS if the conditions in the EXPECT-part are fulfilled.
In contrast to the RULE_FAIL body (see below), in RULE_FORALL you can obtain success messages (such as counter examples) for successful applications of the rule.
RULE_FORALL
list of identifiers
WHERE
conditions on identifiers
EXPECT
conditions that must be fulfilled for this rule
ERROR_TYPE
number encoding error type, must be in range of error types
ON_SUCCESS
STRING_FORMAT("errorMessage ~w", identifier from list) or
```${identifier from list}``` (template string)
COUNTEREXAMPLE
STRING_FORMAT("errorMessage ~w", identifier from list) or
```${identifier from list}``` (template string)
END
Alternatively, a negated rule can be formulated. Here the execution of the rule results in FAIL if the conditions in the WHEN-part are fulfilled.
RULE_FAIL
list of identifiers
WHEN
conditions on identifiers for a failing rule
ERROR_TYPE
number encoding error type, must be in range of error types
COUNTEREXAMPLE
STRING_FORMAT("errorMessage ~w", identifier from list)
END
Counterexamples are of the type INTEGER <-> STRING. The integer contains the error type, while the string contains the message of the counterexample.
Also valid for the rules header are:
RULEID id CLASSIFICATION identifier TAGS identifier
The CLASSIFICATION keyword can be used to group the rules in the HTML validation report according to their classification.
Computations
Computations can be used to define variables. As for rules, their activation can depend on further rules, computations or any other predicate specified as an activation condition. Again, the activation condition is evaluated at initialisation and sets the computation status variable to COMPUTATION_DISABLED if the predicate is false. Furthermore, a DUMMY_VALUE can be set, which initialises the variable with the specified value instead of the empty set before execution of the computation. This mechanism implies that each variable defined by a computation must be a set of type POW(S) for any TYPE S (note: the TYPE section is optional since ProB parser version 2.15.1). A computation can be replaced by a previously defined computation if it sets the same variable (of the same type) by using REPLACES. The general syntax for computations is:
COMPUTATION computation_name
DEPENDS_ON_RULE list of rules
DEPENDS_ON_COMPUTATION list of computations
ACTIVATION predicate
REPLACES identifier of exactly one computation
BODY
DEFINE variable_name
TYPE type of variable
DUMMY_VALUE value of variable before execution (initialisation)
VALUE value of variable after execution
END
END
Activation predicates, dependencies, and also the dummy value can be omitted if they are not needed. After the execution of a computation, the value of the corresponding variable computation_name is changed from NOT_EXECUTED to EXECUTED and the variable variable_name has the value \texttt{VALUE}. For related computations, it may be useful to use multiple DEFINE blocks in one computation.
Separated by ;, the body of a computation can contain any number of variable definitions.
Functions
Functions can be called from any rules machine that references the machine containing the function. Depending on input parameters that must fulfil specified preconditions, the functions returns output value(s) that must fulfil optional postconditions. In the body, any B statement can be used to (sequentially) compute the output value.
FUNCTION output <-- function_name(list of input parameters)
PRECONDITION
predicate
POSTCONDITION
predicate
BODY
some B statements
output := ...
END
Additional Syntax
There are some useful predicates available in rules machines that can be used to check the success or failure of rules. It is also possible to check whether a certain error type was returned by a rule. These are:
SUCCEEDED_RULE(rule1): TRUE, if the check of rule1 succeededSUCCEEDED_RULE_ERROR_TYPE(rule1,1): TRUE, if the check of rule1 did not fail with error type 1GET_RULE_COUNTEREXAMPLES(rule1): set of counterexamples of rule1FAILED_RULE(rule1): TRUE, if the check of rule1 failedFAILED_RULE_ERROR_TYPE(rule1,2): TRUE, if check of rule1 failed with error type 2FAILED_RULE_ALL_ERROR_TYPES(rule1): TRUE, if the check of rule1 failed with all possible error types for rule1NOT_CHECKED_RULE(rule1): TRUE, if rule1 has not yet been checkedDISABLED_RULE(rule1): TRUE, if rule1 is disabled (its preconditions are not fulfilled)
Another functionality of rules machines are FOR-loops. Their syntax is:
FOR variable(s) IN set
DO
operation(s)
END
An example:
RULE example_rule
BODY
FOR x,y IN {1 |-> TRUE, 2 |-> FALSE, 3 |-> FALSE} DO
RULE_FAIL
WHEN y = FALSE
COUNTEREXAMPLE STRING_FORMAT("example_rule_fail: ~w", x)
END
END
This rule always fails and returns {1 |-> "example_rule_fail: 2", 1 |-> "example_rule_fail: 3"}.
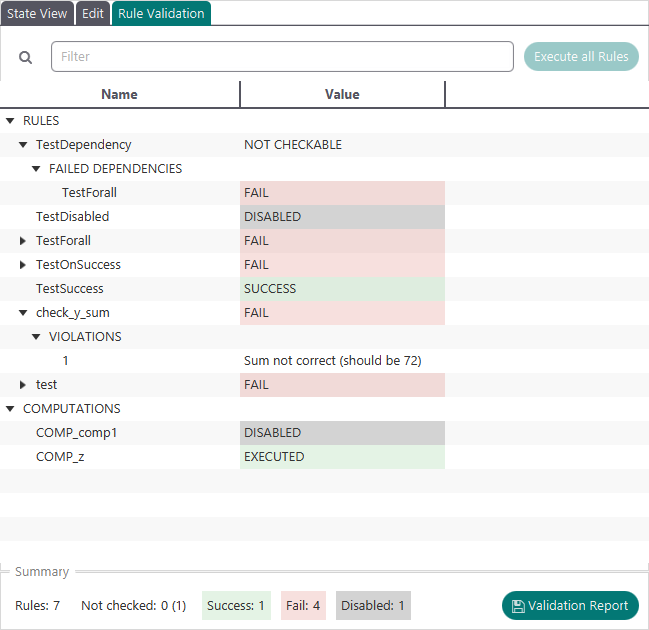
Rule Validation in ProB2-UI
Rule validation has been integrated into the ProB2-UI since version 1.2.2 (not yet released). It allows convenient execution of rules and computations together with a graphical representation of the results. Rules are grouped by their classification and can be additionally filtered by their name, ID, or tags. The results can also be exported as an HTML report. In addition, dependencies of rules and computations can be visualised as a graph either for all operations or for just one operation (the HTML report and the dependency graph are generated by the ProB Java API and can also be created without ProB2-UI).
Rule Validation with probcli
The probcli recognises the option -rule_report <file> which generates the same HTML/XML validation report as in ProB2-UI for the current animation state.
The provided file extension is used to determine whether the HTML or the XML version of the report is generated.
To validate all rules, use this option in combination with -execute_all.
There is also a dot visualisation command "rule_dependency graph" that can be used to create a graph of the dependencies of rules and computations (including results of the current state); example call:
probcli myMch.mch -execute_all -rule_report myReport.html -dot "rule_dependency_graph" myGraph.pdf
All three export options are also available in ProB Tcl/Tk via the visualization menu.
Using the special definition RULE_REPORT_CONTEXT you can include context information about the check in the report (of the type STRING), e.g. the file name of a validated XML file.
Use Rules for Data Validation
The concept of rule validation can be used to validate data from external sources such as CSV or XML files and load the validated data into ProB by successive computations. For an XML file, this could look as follows:
RULES_MACHINE XML_import
DEFINITIONS
"LibraryXML.def"
CONSTANTS
xml_data
PROPERTIES
xml_data = READ_XML("xml_file.xml", "auto")
END
Now some properties can be validated. For example:
RULE is_supported_version_of_type_xyz
ERROR_TYPES 2
BODY
RULE_FAIL e
WHEN
1 : dom(xml_data) & e = data(1)'element & e /= "xyz"
ERROR_TYPE 1 // optional: 1 is standard type
COUNTEREXAMPLE
STRING_FORMAT("Error: could not find element 'xyz', was '"^e^"'")
END;
RULE_FAIL v
WHEN
v = xml_data(1)'attributes("version") & v /: supported_versions
ERROR_TYPE 2
COUNTEREXAMPLE
"xyz of version "^v^" is currently not supported"
END
END;
Internal Representation
Each rules machine is internally translated to an ordinary B machine, which can be accessed as its internal representation. Consider the following example rule:
RULE rule1 BODY RULE_FAIL WHEN bfalse COUNTEREXAMPLE "" END END;
COMPUTATION comp1
BODY
DEFINE x
TYPE POW(INTEGER)
VALUE 1..10
END
END;
RULE rule2
DEPENDS_ON_RULE rule1
// DEPENDS_ON_COMPUTATION comp1
BODY
RULE_FORALL i
WHERE i : 1..10
EXPECT i > 5
COUNTEREXAMPLE STRING_FORMAT("~w <= 5", i)
END
END
Its internal representation in classical B is the following:
`$RESULT`,`$COUNTEREXAMPLES` <-- rule1 =
SELECT
rule1 = "NOT_CHECKED"
THEN
rule1,`$RESULT`,`$COUNTEREXAMPLES` := "SUCCESS","SUCCESS",{}
END;
comp1 =
SELECT
comp1 = "NOT_EXECUTED"
THEN
x,comp1 := FORCE(1 .. 10),"EXECUTED"
END;
`$RESULT`,`$COUNTEREXAMPLES` <-- rule2 =
SELECT
rule2 = "NOT_CHECKED"
& rule1 = "SUCCESS"
& comp1 = "EXECUTED"
THEN
rule2,`$RESULT`,`$COUNTEREXAMPLES` := "SUCCESS","SUCCESS",{} ;
VAR `$ResultTuple`,`$ResultStrings`
IN
`$ResultTuple` := FORCE({i|i : x & not(i > 5)}) ;
`$ResultStrings` := FORCE({`$String`|`$String` : STRING & #i.(i : `$ResultTuple` & `$String` = FORMAT_TO_STRING("~w <= 5",[TO_STRING(i)]))});
rule2_Counterexamples := rule2_Counterexamples \/ {1} * `$ResultStrings` ;
IF `$ResultTuple` /= {} THEN
rule2,`$RESULT`,`$COUNTEREXAMPLES` := "FAIL","FAIL",rule2_Counterexamples
END
END
END
Observe that the implicit dependency of rule2 on comp1 (rule2 uses its variable x) is detected automatically without explicit declaration.
Include Rules Machines into other Projects
Currently, it is not possible to include rules machines directly into any other machines. Instead, use the rules machine at the top of the hierarchy (of the rules project) and save the internal generated machine as .mch-file. After changing the machine name accordingly, the rules can be included and used via this machine.
Note that in this case it is not possible to perform Rules-DSL specific methods of the ProB Java API (like detailed information about rule results).