Induction Proofs in B: Difference between revisions

Induction and B

The classical B and Event-B method are both rooted in classical predicate logic and do not have an explicit inference rule for induction. Note that the B proof rules for invariant preservation are an induction proof in disguise, i.e, the induction is provided by the POG (Proof Obligation Generator) and not the prover itself. They require coding your problem and induction steps as B operations (see the end of this page for one way to do this). Here, I am interested in proving properties in B directly using induction without the help of an external POG.

It is well known that predicate logic is too weak to axiomatize exactly the natural numbers or concepts such as the transitive closure: The transitive closure of a binary relation cannot, in general, be expressed in first-order logic (FO) (Source: Wikipedia).

So, can we perform induction proofs within the B language, without resorting to provers such as Isabelle? The answer is, maybe surprisingly, yes. The reason is that B is not just rooted in predicate logic, but has access to arithmetic and set theory. As such, induction comes "bundled" with the arithmetic operators and data types, more precisely with the well-founded nature of the natural number and the concept of the minimum of a set.

Let us look at one of the classic examples used to illustrate induction proofs, proving the formula for the consecutive sum of natural numbers (see Wikipedia):

• the sum of the numbers from 1 to n is equal to (n*(n+1)) / 2

A finite instance for ProB

We can write a small Event-B model in Rodin (using Camille syntax) like this. Note, as in Rodin the Sigma operator for summing is not pre-defined, I axiomatise the summing up using the constant sum This model computes the sum until a given limit lim It is made finite to be able to be validated using ProB.

context InductiveSum
constants sum lim
axioms
 @axm1 lim∈ℕ1
 @axm2 sum∈ 1‥lim → ℕ
 @axm3 sum(1)=1
 @axm4 ∀i·(i∈2‥lim ⇒ sum(i)=sum(i−1)+i)
 theorem @thm1 ∀i·(i∈1‥lim ⇒ sum(i) = (i∗(i+1))÷2)
 @prob lim=100
 end

We can load this model with ProB, and check that the property holds for all numbers until 100:

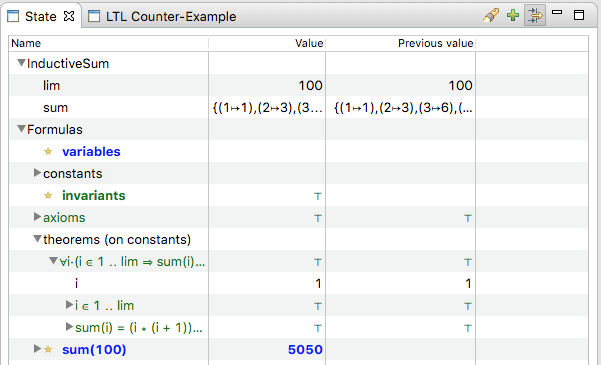
The theorem is the property we wish to prove by induction for any number i>0. How can this be done?

A generic induction proof

I describe here a "trick" that was shown to me by Dominique Cansell many years ago. It relies on specifying your property as a set of natural numbers. Let us first write a small generic Rodin context, which just describes the ideas of the induction proof:

context InductiveProp
constants P Q
axioms
 @axm1 P ⊆ ℕ1
 @axm2 Q ⊆ ℕ1
 @base 1∈P // the base case of the induction
 @induct ∀i·(i>1 ∧ i−1∈P ⇒ i∈P) // the induction step
 @axmq Q = ℕ1 ∖ P // define the elements not satisfying the inductive property
 theorem @concl1 Q=∅ // proof by contradiction using min(Q) in induct for i
 theorem @concl2 P=ℕ1
end

Here P is the property we wish to hold for all natural numbers ≥ 1. We stipulate the base of the induction proof as an axiom here:

we assume we have prove that 1 is an element of P in the axiom @base

We also assume that we have proven the induction step in the axiom @induct, namely that i-1 in P implies that i is in the property P. Our proof target ins the theorem @concl2: that P must hold for all natural numbers ≥ 1.

One crucial idea is to introduce the set Q of properties for which the property does not hold and prove that it is empty. Rodin can automatically discharge @concl2 from @concl1. However, to discharge @concl1 we need to apply the crucial "trick".

The trick is as follows:

• do a proof by contradiction
• this implies that Q is not empty is in the hypotheses
• this implies that min(Q) is well-defined
• this implies that we can instantiate the induction quantifier for i = min(Q)

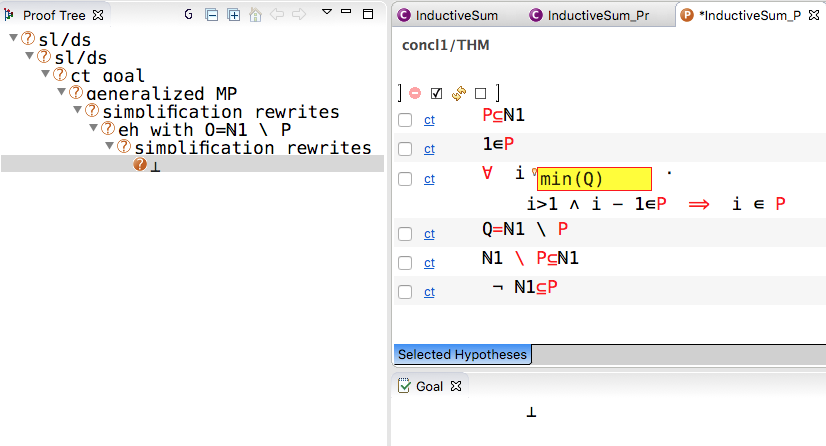
• this allows us to find a contradiction in the hypothesis, given that min(Q)-1 is in P

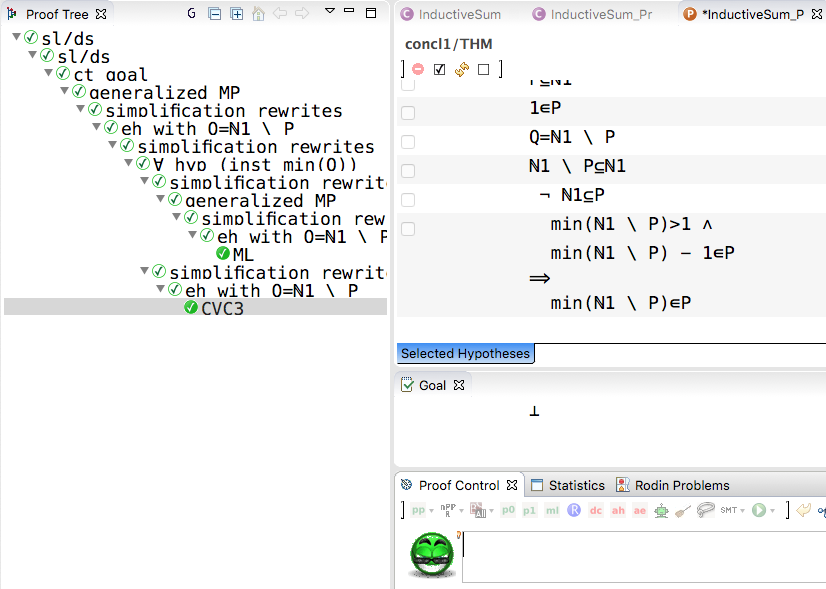
The proof above is very similar to, e.g., the proof of Theorem 1.7.1 on page 17 of the book "The Joy of Sets" by Keith Devlin or the proof in https://proofwiki.org for well-ordered sets: there a proof by contradiction is conducted, using the fact that

the complement NAT1 \ P  is non-empty and choosing the minimal element of the complement to arrive at a contradiction.

The full model with the inductive proof

We integrate this idea with the sum property into a single model as follows:

context InductiveSum_Prop
constants sum P Q
axioms
 @axm2 sum∈ ℕ1 → ℕ
 @axm3 sum(1)=1
 @axm4 ∀i·(i>1 ⇒ sum(i)=sum(i−1)+i)

 @axm5 P ⊆ ℕ1
 @axm6 P = {i∣i∈ℕ1 ∧ sum(i) = (i∗(i+1))÷2}

 theorem @base 1∈P
 theorem @induct ∀i·(i>1 ∧  i−1∈P ⇒ i∈P)

 @axmq1 Q ⊆ ℕ1
 @axmq2 Q = ℕ1 ∖ P // define the elements not satisfying the inductive property
 theorem @concl1 Q=∅ // proof by contradiction using min(Q) in induct for i
 theorem @concl P=ℕ1

 theorem @thm1 ∀i·(i∈ℕ1 ⇒ sum(i) = (i∗(i+1))÷2)
end

You can notice that this time the induction base and step are not axioms but are theorems which thus need to be proven. They need to be proven from the definition of the property P in @axm6 and the definition of sum in @axm3 and @axm4 The induction step is slightly tedious, as the provers are not very powerful concerning integer division. However, it can be done. The proof of the theorems @concl1 is as describe above. The theorems @concl2 and also @thm1 can be discharged automatically by Rodin.

In the end the proofs are all discharged without the help of a inductive prover, just using the standard provers of Rodin (I used the Atelier-B provers and the SMT plugin):

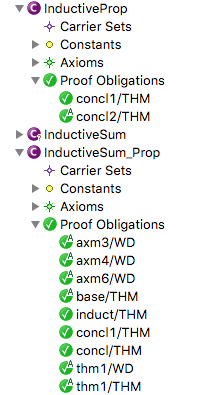
This example can also be conducted within Atelier-B. In fact, Dominique Cansell showed me the "trick" at the time within AtelierB (within the B4Free version).

Additional Discussions

Below we provide two additional discussions, one about how to encode induction using B operations and the B proof obligations, and one about induction and pure predicate logic.

Encoding the Problem as a B Operation

Here is how we can encode our property about the consecutive sums using a B operation to perform the computation of the sum values. The property we wish to prove by induction is @inv3:

machine SumAsOperation
variables i sum
invariants
 @inv1 i∈ℕ1
 @inv2 sum ∈ ℕ
 @inv3 sum = ( i∗ (i+1) ) ÷ 2
events
  event INITIALISATION begin
     @ini i,sum ≔ 1,1
  end
  event compute_next_sum begin
    @inci i≔i+1
    @sum sum ≔ sum+i+1
  end
end

Here is the machine when animated by ProB:

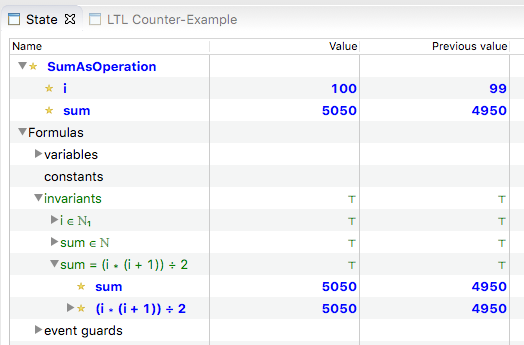
The Rodin POG generates the proof obligations for the induction:

• INITIALISATION/inv3/INV: 1=(1+1)/2
• compute_next_sum/inv3/INV: sum+i+1=(i+1)∗((i+1)+1) ÷ 2

The induction principle itself is here outside of the B provers: the provers are used to discharge the above proof obligations, not to prove that they entail that the invariant is true in all reachable states.

Induction and Pure Predicate Logic

Let us try and encode natural numbers using predicate logic:

• zero is a natural number
• if x is a natural number then its successor is a natural number Nothing else is a natural number.

We encode the set of natural numbers using the variable nat which is a subset of some domain 𝐷 D . The successor function is a total function over the domain D.

 s∈D-->D & zero:D & nat ⊆ D ∧ 
 zero ∈ nat ∧
 ∀x.(x∈nat ⇒ s(x):nat)

This always allows nat=D as solution. One can try and improve the encoding by using an equivalence:

D=BOOL ∧ s∈D-->D ∧ zero:D ∧ nat ⊆ D ∧ 
∀x.(x∈D ⇒ (x∈nat ⇔ (x=zero ∨ (∃y.(x=s(y) ∧ y∈nat)))))

Does the induction principle hold in this axiomatisation of the natural numbers? Let's try it out. We put the above into a context, add the inductive property P,

stipulating that zero is in P and that if z is  in P then its successor is also in P.

context InductionAndPredicateLogic
sets D // our domain
constants s zero nat P
axioms
 @axm1 s∈D→D
 @axm2 zero∈D
 @axm3 nat ⊆ D
 @axm4 ∀x·(x∈D ⇒ (x∈nat ⇔ (x=zero ∨ (∃y·(x=s(y) ∧ y∈nat)))))
 @axm5 P ⊆ D // P is our property, we wish to prove that nat ⊆ P
 @axm6 zero∈P  // induction base
 @axm7 ∀z·(z∈P ⇒ s(z)∈P) // induction step

 @invalid ¬(nat ⊆ P)  // the induction does not hold
end

The last axiom is the negation of the conclusion of the induction theorem. If ProB can load the above context, then the induction principle does not hold for this axiomatisation. And indeed, it does not:

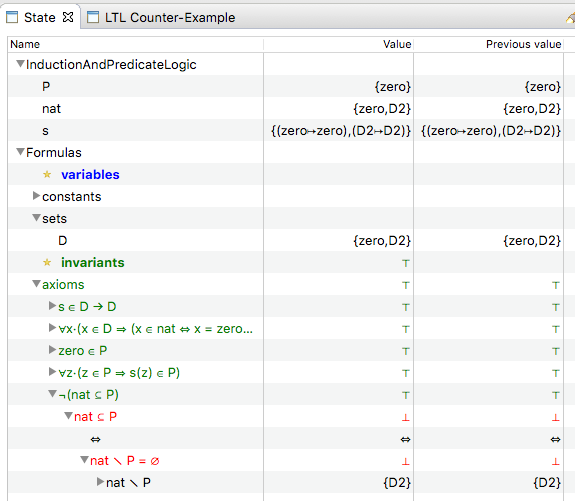
Comment: One can go even further and introduce Clark's Equality Theory to stipulate that s(x) is different from zero,... But this does not solve the problem. It cannot be solved in pure predicate logic.

But as shown above, in B we have directly access to the set of natural numbers and to the min operator; hence we can conduct valid induction this way.