Induction Proofs in B: Difference between revisions
No edit summary |
No edit summary |
||
| Line 33: | Line 33: | ||
The theorem is the property we wish to prove by induction. | The theorem is the property we wish to prove by induction. | ||
How can this be done? | How can this be done? | ||
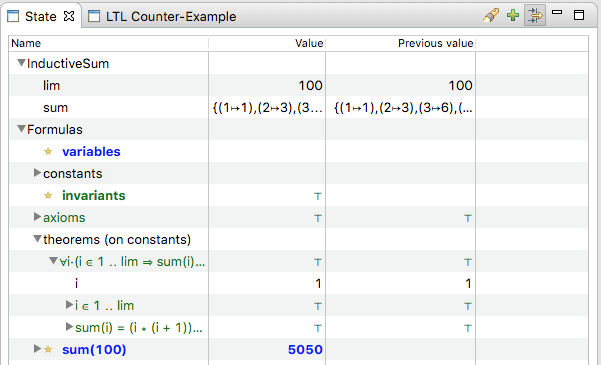
[[File:ProB_Induction_Screenshot1.png|600px|center]] | |||
Revision as of 16:53, 21 April 2020
The classical B and Event-B method are both rooted in classical predicate logic and do not have an explicit inference rule for induction. The B proof rules for invariant preservation are an induction proof in disguise, but that is another story. They require coding your problem and induction steps as B operations. Here, I am interested in proving properties in B directly using induction. Can this be done at all, without resorting to provers such as Isabelle? The answer is, yes. The reason is that B is not just rooted in predicate logic, but has access to arithmetic and set theory. As such, induction comes ``bundled with the arithmetic operators and data types.
Let us look at one of the classic examples used to illustrate induction proofs, proving the formula for the consecutive sum of natural numbers (see Wikipedia):
- the sum of the numbers from 1 to n is equal to (n*(n+1)) / 2
We can write a small Event-B model in Rodin (using Camille syntax) like this. Note, as in Rodin the Sigma operator for summing is not pre-defined, I axiomatise the summing up using the constant sum This model computes the sum until a given limit lim It is made finite to be able to be validated using ProB.
context InductiveSum constants sum lim axioms @axm1 lim∈ℕ1 @axm2 sum∈ 1‥lim → ℕ @axm3 sum(1)=1 @axm4 ∀i·(i∈2‥lim ⇒ sum(i)=sum(i−1)+i) theorem @thm1 ∀i·(i∈1‥lim ⇒ sum(i) = (i∗(i+1))÷2) @prob lim=100 end
The theorem is the property we wish to prove by induction. How can this be done?